Квадратные неравенства: решение с помощью эскиза графика квадратичной функции; решение методом интервалов — (8 ч).

О с н о в н а я ц е л ь — сформировать понятие квадратного неравенства; сформировать умение решать квадратные неравенства с помощью эскиза графика квадратичной функции; дать представление о решении методом интервалов.

Организуется усвоение определений квадратного неравенства, равносильных неравенств, равносильных преобразований неравенств, алгоритма решения квадратных неравенств с помощью эскиза графика квадратичной функции. На конкретных примерах осуществляется знакомство с решением неравенств методом интервалов.

Элементы статистики, теории вероятностей и комбинаторики — (6 ч).

Математическое ожидание случайной величины и наиболее вероятные значения. Понятие среднего значения. Экспериментальное отыскание среднего значения. Множество. Элементы множества.

Повторение. Решение задач — (4 ч).

Класс

(3 ч в неделю, всего 102 ч)

Системы неравенств: неравенства с модулями; системы, включающие двойные и квадратные неравенства — (8 ч).

О с н о в н а я ц е л ь — повторить и закрепить на новом уровне решение систем неравенств первой степени, работу с модулями, решение квадратных неравенств методом интервалов; познакомить с возможностью воспользоваться ранее полученными знаниями для решения систем, включающих двойные и квадратные неравенства.

Изучение темы в большой мере сводится к повторению и закреплению ранее изученного в ходе решения задач более сложных, чем в 8 классе.

Уравнения и системы уравнений второй степени: уравнения, приводимые к квадратным; иррациональные уравнения; уравнения с модулями; решение систем уравнений второй степени; решение задач с помощью систем уравнений второй степени — (20 ч).

О с н о в н а я ц е л ь — познакомить с решением методом разложения на множители и введения вспомогательной переменной уравнений с одним неизвестным, степень которых выше второй; выработать умение решать простейшие системы, содержащие уравнения второй степени с двумя переменными; и текстовые задачи с помощью составления таких систем.

Данная тема завершает изучение рациональных уравнений с одной переменной. Учащиеся знакомятся с решением некоторых уравнений, степень которых больше 2, с помощью разложения на множители и введения вспомогательной переменной.

В данной теме вводится понятие иррационального уравнения и алгоритмы, позволяющие решить простейшие такие уравнения.

Продолжается обучение решению уравнений, содержащих модуль неизвестного. Учащиеся знакомятся с решением систем, включающих уравнения и неравенства. Осуществляется закрепление и углубление знакомства с методом интервалов.

Рассматриваются системы, содержащие уравнения второй степени с двумя неизвестными. Основное внимание уделяется системам, в которых одно уравнение первой степени, а другое — уравнение второй степени. Известный учащимся способ подстановки позволяет свести решение такой системы к решению квадратного уравнения. Решение уравнений второй степени с двумя неизвестными, в которых оба уравнения второй степени, не является обязательным материалом.

3. Арифметическая и геометрическая прогрессии: способы задания последовательностей; формула n-го члена арифметической и геометрической прогрессий; формула суммы первых n членов арифметической и геометрической прогрессий; сумма бесконечной геометрической прогрессии, у которой |q| < 1; задачи на прогрессии — (28 ч).

О с н о в н а я ц е л ь — дать представление о числовых последовательностях и способах их задания; сформировать понятие об арифметической и геометрической прогрессиях как числовых последовательностях особого вида; научить пользоваться формулами для вычисления n-го члена и суммы первых n членов арифметической и геометрической прогрессий.

Последовательность вводится как функция f(n), заданная на любой части множества натуральных чисел. Рассматриваются различные способы задания последовательностей. Особое внимание уделяется рекуррентному способу задания и выработке умения использовать индексные обозначения.

При выводе формул для вычисления n-го члена арифметической и геометрической прогрессий дается первоначальное представление о методе полной математической индукции.

Сведения о бесконечно убывающей геометрической прогрессии не являются обязательными для изучения.

4. Степень с рациональным показателем: степенные функции вида у = хⁿ;график уравнения окружности; графическое решение уравнений и систем уравнений; корни третьей и четвертой степени. Понятие о корне n-ой степени из числа; арифметический корень n-ой степени из числа и его свойства; степени с дробным показателем и их свойства; тождественные преобразования выражений, содержащих корни и степени — (16 ч).

О с н о в н а я ц е л ь — дать представление о степенных функциях и их графиках; о графическом решении уравнений и систем уравнений, степень которых выше первой; познакомить с понятиями корня n-ой степени из числа, степени с дробным показателем и их свойствами.

При знакомстве с графиками степенных функций и их свойствами самое главное — повторить и закрепить уже известные ученикам сведения о свойствах функций и особенностей их графиков. Доказательства теорем о четности или нечетности степенных функций, о возрастании или убывании степенных функций не являются обязательными.

График уравнения окружности дается в рассматриваемой теме потому, что умение строить окружность расширяет возможности графического решения уравнений и систем уравнений.

Знакомство с понятием корня n-ой степени из числа можно ограничить обеспечением понимания той связи, которая существует между функциями у = 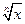и у = хⁿ и между соответствующими графиками обратных функций.

Свойства корней n-ой степени из числа — материал не обязательный.

Усвоению подлежит определение степени с дробным показателем 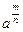. Достаточно, чтобы ученики понимали: свойства любых степеней с рациональными показателями такие же, как свойства степеней с натуральными показателями. Доказательство этого факта — материал не обязательный.