Потери напора на Местных сопротивлениях

Потери напора на местных сопротивлениях определяются по формуле:

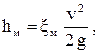(2.13)

где v - средняя скорость движения жидкости;

ξ_м - коэффициент местного сопротивления.

Потеря напора на местном сопротивлении может определяться как по скорости до местного сопротивления, так и по скорости после местного сопротивления. Так как скорости по величине могут быть разными, то в этих случаях для одного и того же местного сопротивления будут разные значения ξ_м. принято определять потери напора по скорости после местного сопротивления. Исключение составляет расширение трубопровода (выход потока из трубы в бак), где потери определяются по скорости до местного сопротивления.

Замковые соединения труб представляют собой сужение и расширение потока и поэтому представляют собой сумму потерь напора на сужение и расширение. Эти потери напора будем определять по скорости до замкового сопротивления, тогда коэффициент на сужение определяется по формуле

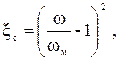(2.14)

а для расширения по формуле

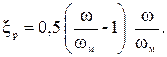(2.15)

Здесь w - площадь поперечного сечения до замка, w_м - минимальная площадь поперечного сечения в замке.

Число замковых соединений зависит от глубины скважины и длины одной трубы НКТ n = L/L_НКТ. Тогда коэффициент сопротивления на всех замках будет равен:

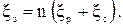(2.16)

Коэффициент сопротивления штуцера зависит от отношения площадей поперечных сечений отверстия штуцера w_ш и труб арматуры w_а на устье скважины (диаметр труб арматуры принимается равным 63 мм) и определяется по таблице 2.1.

Таблица 2.1 – Определение коэффициента сопротивления штуцера

wш/wа	0,05	0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9	1,0
xш			51,2	18,2	8,25	4,0	2,0	0,97	0,42	0,13	0,0

С учетом разных площадей поперечного сечения скважины и арматуры коэффициент сопротивления штуцера определяется по формуле

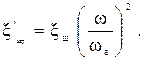(2.17)

Потери напора в некруглых трубах

При движении жидкости по трубам некруглого сечения расчет производится с учетом следующих особенностей.

Вводится понятие эквивалентного диаметра D_э:

D_э = 4 w /χ, (2.18)

где w - площадь сечения;

χ - смоченный периметр - это часть периметра живого сечения, где жидкость соприкасается со стенками.

Для кольцевого пространства с диаметрами D и d площадь, смоченный периметр и эквивалентный диаметр равны:

w = π (D² – d²)/4;

χ = π (D + d); (2.19)

D_э = 4 w /χ = (D - d).

При расчете потерь напора и числа Рейнольдса в формулах (2.8) и (2.7) вместо диаметра D подставляется эквивалентный диаметр D_э. Средняя скорость в трубе определяется v = Q/w .

Движение газа по трубам

Малые перепады давлений. Если перепад давления мал, т.е. (р₁ - р₂)/р₁ = 0,1, то в этом случае с точностью до 10% можно сжимаемостью газа пренебречь и расчет вести как для несжимаемой жидкости. Для расчета необходимо найти среднее давление р_ср в колонне труб, среднюю температуру Т_ср, среднее значение коэффициента сверхсжимаемости z_ср (для идеального газа z_ср = 1). Так как давление на забое скважины неизвестно, то в первом приближении давление на забое скважины можно принять равным пластовому. Считая температуру газа на поверхности равной 20°С (293°К), а пластовую температуру Т_пл, получим:

р_ср = 0,5 (р_у + р_з), Т_ср = 0,5 (293 + Т_пл). (2.20)

Движение газа считается изотермическим, поэтому средняя плотность идеального газа находится как

ρ_ср = ρ_ат р_ср Т_ат/(р_ат Т_ср). (2.21)

где р_ат - атмосферное давление, принимается равным 0,1 МПа;

ρ_ат - плотность газа при стандартных условиях;

Т_ат - стандартных температура (293°К).

Объемный расход, приведенный к среднему значению давления и температуры в скважине, определится по формуле

Q = Q_ат ρ_ат /ρ_ср , (2.22)

а средние скорости движения газа

v = Q/w. (2.23)

Дальнейший расчет ведется аналогично расчету движения несжимаемой жидкости. По окончании расчета будет найдено в первом приближении давление на забое скважины. После этого найдем уточненное значение среднего давления и средней плотности газа по формулам (2.20, 2.21) и в ходе расчета найдем новое значение забойного давления. Таким образом, дальнейшие расчеты продолжать до тех пор, пока значение старого и нового забойного давления будут отличаться не более чем на 1%.

Большие перепады давлений. Если перепад на забое и устье большой, т.е. (р₁ - р₂)/р₁ > 0,1, то в этом случае удобно пользоваться формулой Адамова. Для расчета необходимо найти среднее давление р_ср в колонне труб, среднюю температуру Т_ср, среднее значение коэффициента сверхсжимаемости z_ср (для идеального газа z_ср = 1). Так как давление на забое скважины неизвестно, то в первом приближении давление на забое скважины можно принять равным пластовому. Считая температуру газа на поверхности равной 20°С (293°К), а пластовую температуру Т_пл получим

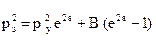, (2.24)

здесь

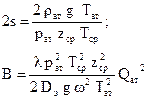(2.25)

Коэффициент гидравлического сопротивления трения рассчитывается по формулам раздела 2.3, только число Рейнольдса удобнее рассчитывать по формуле:

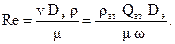(2.26)

Порядок расчета

1). Задаемся максимальными значениями расхода. Расход (дебит) нефтяных и газовых скважин зависит от диаметра труб, перепада давления, вязкости, проницаемости пласта и многих других причин. Поэтому максимально возможные значения расхода (дебита) данной скважины задать, даже ориентировочно, трудно. Например, на Усинском месторождении дебит нефтяных скважин составляет от 10 до 100 м³/сут. Для газовых скважин значение приведенного дебита, например, на Вуктыльском месторождении, порядка 10⁵ м³/сут.

2). При заданном максимальном расходе (дебите) определяют среднюю скорость движения жидкости (газа) (п. 2.2), число Рейнольдса (п. 2.3), коэффициент гидравлического сопротивления трения (п. 2.3), коэффициент местных сопротивлений, потери напора и находят значение давления на забое скважины. При расчете движения газа в скважине, порядок расчета определения забойного давления определяется согласно пункту 2.6.

3). Задаемся значениями расхода (дебита), которые составляют 0,8; 0,6; 0,4; 0,2 и 0 от максимального значения расхода (дебита). Расчет производится аналогично пункту 2).

4). Результаты расчета удобно оформить в виде таблицы (таблица 2.2). В столбце примечаний указываются значения коэффициентов местных сопротивлений, вязкости жидкости, плотности газа при атмосферных условиях.

5). На основании расчетов строится зависимость забойного давления от расхода (рисунок 3.3).

Таблица 2.1 – Результаты расчетов

№№ по п.п.	Расход Q	Плотность ρ (ρат)	Скорость v = Q/ω	Число Рейнольдса Re	Режим движения	Коэффициент гидравлического сопротивления трения λ	Потери напора между сечениями 1 и 2 h1-2	Забойное давление Pз	Примечание
	м3/с	кг/м3	м/с	-	-	-	м	МПа
1.
2.
3.
4.
5.
6.

Замечание. Нулевое значение расхода берется обязательно.