Пояснить в чем сущность метода деления отрезка пополам, применяемого для нахождения оптимальных точек функции.

Метод деления отрезка пополам.Пусть дано уравнениеf(x)=0, функция f(x) непрерывна на интервале [a,b]. Условие f(a)*f(b)<0 указывает тогда на наличие хотя бы одного корня на этом отрезке.

Поделим отрезок [a,b] пополам точкой c, координата которой c=(a+b)/2 и вычислим значение функции f(c). Возможны два случая: а) f(a)*f(c)>0, т.е. значения функции на концах отрезка [a, c] одинаковы по знаку; тогда корень уравнения находится на отрезке [c, b] и отрезок [a, c] можно исключить из дальнейшего рассмотрения, перенеся точку a в точку c:a=c; f(a)=f(c) (рис. а);

б) f(a)*f(c)<0, т.е. значение функции на концах отрезка [a, c] противоположны по знаку; тогда корень находится на отрезке [a, c] и отрезок [c, b] можно исключить из дальнейшего рассмотрения, перенеся точку bв точку c:b=c (рис. б). После исключения правой или левой половины отрезка продолжают деление пополам до тех пор, пока длина оставшегося интервала [a, b] не станет меньше некоторой заданной малой величины , т.е.|b-a|< , и тогда любое значение аргумента из отрезка [a, b] можно считать корнем с погрешностью . Обычно принимают в качестве корня середину отрезка.

Отметим, что здесь имеет смысл допустимой абсолютной погрешности вычисления корня. Достоинством метода является его безусловная сходимость, если на интервале [a, b] имеется хотя бы один корень. Кроме того, метод не использует производных. К недостаткам относят медленную сходимость, т.е. достаточно большое число вычислений функции f(x)по сравнению с другими методами. Рекомендуется к использованию в тех случаях, если нет жестких требований ко времени счета

Пояснить каковы особенности решения оптимизационных задач в MathCad

В системе MathCAD такие задачи решаются с помощью блоков Given-Maximize и Given-Minimize. Так же, как и при решении систем уравнений, решающий блок состоит из нескольких компонент, в строго определенном порядке:

1. Присваивание начальных значений переменным, относительно которых решается задача оптимизации.

2. Определение целевой функции.

3. Директива Given.

4. Ограничения, записываемые в обычной математической форме. Могут использоваться все знаки отношений, но вместо простого знака равенства «=» используется оператор логического равенства (вводится путем нажатия Ctrl-=). Замечание: система MathCAD при минимизации и максимизации воспринимает знаки строгого неравенства (<,>) как знаки нестрогого неравенства .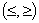

5.Обращение к одной из функций Minimize или Maximize для соответственно минимизации или максимизации. Первым аргументом всегда является имя целевой функции. Далее следуют имена переменных, относительно которых решается задача. Функция возвращает вектор значений, где первый элемент соответствует первой переменной в списке аргументов, второй элемент - второй переменной и так далее.