Дать характеристику метода линейной регрессии: описание метода, реализация метода в MathCad.
Линейная регрессия – это метод восстановления зависимости между двумя переменными при помощи линейной функции (прямой вида y=ax+b). Алгоритм линейной регрессии позволяет представить зависимость между зависимой и независимой переменными как линейную, а затем использовать полученный результат при прогнозировании. Подобный пример представлен на рис. 1. Линия на диаграмме является наилучшим линейным представлением данных.
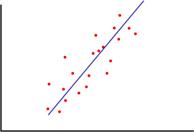
Рисунок 1 – Линейная регрессия
В случае одной независимой переменной (одним регрессором) задача может быть сформулирована следующим образом. Уравнение описывающее линию: y=a+bx. Для i-й точки будет справедливо 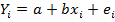 ,
, 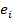 где – разница между фактическим значением
где – разница между фактическим значением 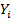 и вычисленным в соответствии уравнением линии. Иначе говоря, каждой точке соответствует ошибка, связанная с ее расстоянием от линии регрессии. Нужно с помощью подбора коэффициентов a и b получать такое уравнение, чтобы сумма ошибок, связанных со всеми точками, стала минимальной. Для решения этой задачи может использоваться, в частности, метод наименьших квадратов (МНК).
и вычисленным в соответствии уравнением линии. Иначе говоря, каждой точке соответствует ошибка, связанная с ее расстоянием от линии регрессии. Нужно с помощью подбора коэффициентов a и b получать такое уравнение, чтобы сумма ошибок, связанных со всеми точками, стала минимальной. Для решения этой задачи может использоваться, в частности, метод наименьших квадратов (МНК).
В MathCAD реализована возможность выполнения линейной регрессии общего вида.Для реализации линейной регрессии общего вида в MathCAD имеется набор функций: intercept и slope, которые возвращают значения коэффициентов прямой без непосредственного задания пользователем формул метода наименьших квадратов. Значения функций Х и У представляются в виде вектор-столбцов VX и VY соответственно.intercept(VX,VY) – возвращает значение параметра а (смещение регрессии по вертикали);slope(VX, VY) – возвращает значение параметраb(наклон линии регрессии);

Пояснить в чем сходство и различие между линейной регрессией и кусочно-линейной интерполяцией.
Линейная регрессия, используется для зависимости одной переменной от другой или нескольких других с линейной функции зависимости. Говоря простым языком, имея значения множество переменных, строиться прямая, которая аппроксимирует данное множество, чтоб отклонение от точек(переменных) было минимальным. Линейная регрессия решается методом наименьших квадратов, то есть необходимо определить параметры a и b, и подставить в уравнение прямой 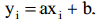
Кусочно-линейная интерполяция способ определения неизвестных промежуточных значений динамического ряда. Самый простой вид интерполяции – линейная, которая представляет искомую зависимость А(Х) в виде ломаной линии. Интерполирующая функция А(х) состоит из отрезков прямых, соединяющих точки. Уравнение такой линии имеет след.вид:
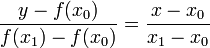 ,
,
Отсюда получаем формулу линейной интерполяции:
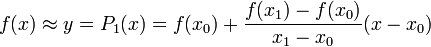
Сходство данных методов, это аппроксимирование виде прямых линий, различие состоит в том, что в отличие ЛР, КЛИ строит прямые по переменным, в итоге получается ломанная линия.
