Пояснить в чем заключается суть статистической обработки данных эксперимента.

Все методы математико-статистического анализа условно делятся на первичные и вторичные. Первичными называют методы, с помощью которых можно получить показатели, непосредственно отражающие результаты производимых в эксперименте измерений. Соответственно под первичными статистическими показателями имеются в виду те, которые применяются в самих психодиагностических методиках и являются итогом начальной статистической обработки результатов психодиагностики. Вторичными называются методы статистической обработки, с помощью которых на базе первичных данных выявляют скрытые в них статистические закономерности.

К первичным методам статистической обработки относят, например, определение выборочной средней величины, выборочной дисперсии, выборочной моды и выборочной медианы. В число вторичных методов обычно включают корреляционный анализ, регрессионный анализ, методы сравнения первичных статистик у двух или нескольких выборок.

Модой называют количественное значение исследуемого признака, наиболее часто встречающееся в выборке. К примеру, в последовательности значений признаков 1, 2, 5, 2, 4, 2, 6, 7, 2 модой является значение 2, так как оно встречается чаще других значений - четыре раза.

Медианой называется значение изучаемого признака, которое делит выборку, упорядоченную по величине данного признака, пополам. Например, для выборки 2, 3, 4, 4, 5, 6, 8, 7, 9 медианой будет значение 5, так как слева и справа от него остается по четыре показателя.

Дисперсия - это среднее арифметическое квадратов отклонений значений переменной от её среднего значения.Дисперсия как статистическая величина характеризует, насколько частные значения отклоняются от средней величины в данной выборке. Чем больше дисперсия, тем больше отклонения или разброс данных.

Регрессию выражают с помощью двух уравнений регрессии, которые в самом прямом случае выглядят, как уравнения прямой.

Y = a 0 + a 1 * X (1)

X = b 0 + b 1 * Y (2)

Метод корреляций показывает, каким образом одно явление влияет на другое или связано с ним в своей динамике. Подобного рода зависимости существуют, к примеру, между величинами, находящимися в причинно-следственных связях друг с другом.

Пояснить какие функции статистической обработки используются для описательной статистики. Дать понятие доверительного интервала.

Описательная статистика позволяет обобщать первичные результаты, полученные при наблюдении или в эксперименте. Все расчеты описательных статистик сводятся к группировке данных по их значениям, построению распределения их частот, выявлению центральных тенденций распределения и к оценке разброса данных по отношению к найденной центральной тенденции.

Цель представления данных в виде описательных статистик – сделать выводы и принять стратегические (для анализа) решения, основанные на имеющихся данных.

Применение описательной статистики включает следующие этапы:

-Сбор данных;

-Категоризация данных;

-Обобщение данных;

-Представление данных.

В рамках описательной статистики применяются следующие простейшие техники:

-Графическое представление данных.

-Табличное представление данных.

-Использование обобщающих статистик, таких, как математическое ожидание, медиана, дисперсия и т.д.

Основные показатели описательной статистики:

· Среднее значение (среднее арифметическое, медиана, мода)

· Усредненное значение

· Разброс (диапазон разброса данных)

· Дисперсия

· Стандартное (среднеквадратическое) отклонение

· Квартили

Доверительным интервалом называется интервал, построенный с помощью случайной выборки из распределения с неизвестным параметром, такой, что он содержит данный параметр с заданной вероятностью.

Доверительный интервал – предельные значения статистической величины, которая с заданной доверительной вероятностью γ будет находится в этом интервале при выборке большего объема. Обозначается как P(θ - ε < x < θ + ε) = γ. Мерой доверия оценке θ считается вероятность γ того, что погрешность оценки |θ - x| не превысит заданной точности ε: 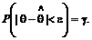.