Анализ результатов всей совокупности проведенных в настоящей работе экспериментов позволяет сформулировать следующий основной тезис, являющийся признаком геометрической прочности произвольной сети.

Признак геометрической прочности произвольной сети. При случайных внешних разрушающих воздействиях, произвольная сеть 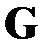попадает в пограничное состояние тогда, когда значение отношения 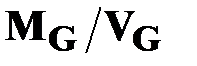близко к единице, то есть когда количество ребер в ней становится численно равно площади сетки, на которой эта сеть размещена.

Экспликация утверждения 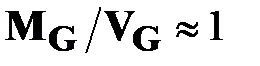, выявленного в результате экспериментов для прямоугольных регулярных сетей, на случай произвольных сетей обосновывается следующими эвристическими соображениями.

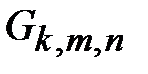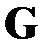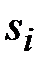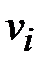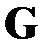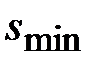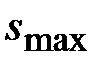Результаты экспериментов настоящей работы относятся к регулярным сетям вида – степени всех вершинодинаковы и равны k . Произвольная сеть , возникающая в практической деятельности,конечно, не обязана быть регулярной, но степени ее вершин , в силу конечности самой сети , ограничены и находятся в диапазоне от и до . Вершины 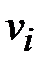рассматриваемой сети 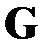можно разместить в узлах прямоугольной 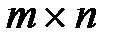сетки на плоскости (см. п.2.3.2). Таким образом, можно представлять себе сеть 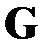как регулярную прямоугольную сеть 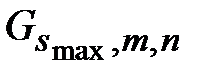, из которой «уже удалены» некоторые ребра. Аналогично, можно мыслить себе сеть 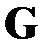как регулярную прямоугольную сеть 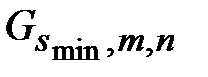, к которой добавлены ребра в подходящих местах.

Сказанное означает, что для разрушения сети 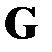в целом, из нее надо случайным образом удалить ребер в среднем не меньше, чем из сети 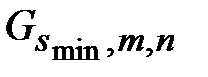, но и не больше, чем из сети 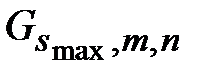. Следовательно, в среднем, для произвольной сети выполняется неравенство:

.

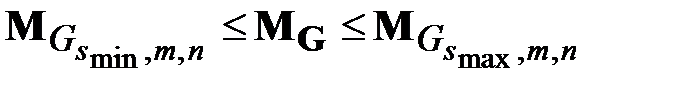После деления на количество вершин 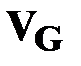, получаем неравенство:

,

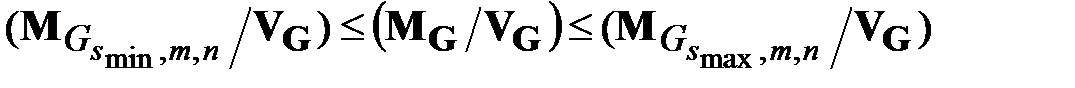которое выполняется для произвольной сети 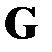в среднем при достаточно больших ее размерах. Поскольку крайние левая и правая части этого неравенства близки к 1, то и средняя часть этого неравенства для реальной сети тоже близка к 1 , то есть .

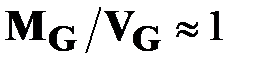Приведенное рассуждение как раз и означает, что для применимых на практике достаточно больших сетей произвольной конфигурации так же справедлив основной тезис настоящей работы. Это означает, что для достижения пограничного состояния или распада произвольной сети 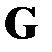в целом, из нее надо случайным образом выбить в среднем примерно 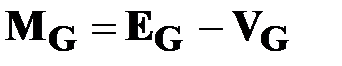штук ребер.

Сформулированный признак геометрической прочности произвольных сетей позволяет сделать фундаментальный и общеприменимый практически важный вывод. При проектировании и практическом строительстве произвольных сетей, для достижения ее геометрической прочности и устойчивости по отношению к разрушающим внешним воздействиям, необходимо добиваться выполнения двух условий:

1) сеть должна быть достаточно регулярной;

2) количество связей в сети должно быть существенно больше числа ее элементов.

Условие 1) означает, что степени всех вершин рассматриваемой сети больше единицы и интервал от 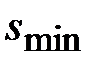до 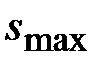не слишком широк. Такая сеть заведомо не содержит «висячих» вершин и фрагментов, разрыв связей с которыми сразу приводит к распаду сети. Условие 1) необходимо для страховки сети от распада при единичных случайных воздействиях, для взаимозаменяемости связей сети и прочности каждого фрагмента сети. Условие 2) обеспечивает запас геометрической прочности сети, гарантирует, что созданная сеть заведомо не находится изначально в критически-пограничном состоянии (когда любое случайное разрушение ребра может привести к распаду сети в целом) и обладает достаточным запасом прочности по отношению к продолжительным внешним разрушающим воздействиям.

Сформулированный признак геометрической прочности сетей является универсальным, допускающим адаптацию и соответствующую формулировку, предназначенную к использованию в каждом конкретном случае практического построения сетевых структур. Например, применительно к области построения сетей коммуникаций и/или транспортных сетей, признак устойчивости к случайным разрушающим воздействиям может быть переформулирован следующим образом: сеть коммуникаций на плоскости прочна (устойчива к случайным внешним разрушающим воздействиям) тогда, когда суммарная длина коммуникаций превосходит площадь района, для обслуживания которого они предназначены.

Выводы по главе 2

1. Многочисленные наработанные к настоящему времени примеры моделей сетевых структур взаимодействия, использовавшиеся ранее для представления и анализа сетевых структур, допускают естественное обобщение и систематизацию на языке общей алгебры и теории алгебраических систем. В настоящей главе приведен один из вариантов такого обобщения – многоосновные мультиоператорные сети, и детально рассмотрена проблематика, касающаяся абстрактных геометрических свойств моделей, полученных в результате предложенного обобщающего подхода.

2. Многоосновные мультиоператорные сети являются новым универсальным и практически удобным инструментом представления и моделирования реальных организационных сетевых структур. Понятие мультиоператорной сети позволяет отражать и моделировать не только внутренние параметры и характеристики сети, ее узлов и связей, но и различные внешние воздействия на моделируемые структуры, их трансформации и преобразования. Такой универсальный динамический подход к представлению и моделированию сетевых структур предлагается в научной литературе впервые.

3. На основе модельного понимания организационных сетей как многоосновных мультиоператорных сетей, выделены и систематизированы два основных класса задач прочности и устойчивости организационных сетей, к которым приводит анализ проблематики прочности и устойчивости мультиоператорных сетей с практической точки зрения. Естественную основу такой систематики дает разделение задач прочности и устойчивости по характеру разрушающих воздействия на сеть (внешние и внутренние воздействия). В рамках предложенного модельного обобщения, эти разрушающие воздействия оказывается возможным формализовать в виде действия на сеть набора сигнатурных операторов.

4. В предложенной общей постановке, задачи прочности и устойчивости мультиоператорных сетей являются новыми, актуальными и перспективными задачами как с прикладной (экономической, организационной и управленческой), так и с чисто научной (математической) точек зрения.

5. На основе общих модельных представлений организационных структур как мультиоператорных сетей, рассмотрена известная задача об определяемости организационных сетей по наборам их геометрических характеристик. Введены новые и обобщены известные ранее группы геометрических характеристик произвольных градуированных организационных сетей.

6. На основании введенных геометрических характеристик, предложен принципиально новый метод представления организационных сетей – метод кортежей. Преимущества нового метода, по сравнению с традиционным матричным представлением сетей – простота, наглядность, легкость восстановления диаграммы сети, простота выполнения стандартных алгоритмов анализа сетей, значительное сокращение объема хранимого числового массива, простота вычисления геометрических характеристик организационных сетей.

7. Приведены естественные геометрические характеристики градуированных организационных сетей, предложены их практические интерпретации и указано, какие реальные процессы в организационных структурах описываются введенными геометрическими характеристиками. Строго доказана полнота и категоричность метода кортежей, чем полностью решена известная задача об определяемости градуированных организационных сетей наборами своих геометрических характеристик.

8. Рассмотрена задача определения геометрической (топологической) прочности произвольных сетей, их устойчивости на разрыв при случайных внешних разрушающих воздействиях на сетевые связи. Эта задача напрямую относится к выделенным и классифицированным в настоящей главе типам задач прочности и устойчивости мультиоператорных сетей. Введены числовые характеристики геометрической прочности сетей, разработаны практически применимые алгоритмы их вычисления и проведены серии компьютерных экспериментов по вычислению значений показателей геометрической прочности для различных типов сетей.

9. На основании анализа проведенных численных экспериментов удалось обнаружить фундаментальные закономерности в процессах разрушения сетей при воздействии случайных внешних факторов. Это позволило сформулировать практически важный и универсальный признак геометрической прочности сетей. Сформулированный универсальный признак позволяет сделать фундаментальный практически важный вывод – при проектировании и практическом строительстве произвольных сетей, для достижения их геометрической прочности и устойчивости по отношению к разрушающим внешним воздействиям, необходимо добиваться выполнения условий регулярности сети и превосходства общей длины связей сети над численным значением её площади.

10. Сформулированный признак геометрической прочности сетей является универсальным, допускающим адаптацию и соответствующую формулировку, предназначенную к использованию в каждом конкретном случае практического построения сетевых структур. Адаптации, уточнения и переформулировки общего признака геометрической прочности сети для различных важных конкретных типов сетей, используемых в практической деятельности, представляют собой перспективные, актуальные и практически важные направления дальнейших исследований.

Литература к главе 2

1. Д.Филлипс, А.Гарсиа-Диас. Методы анализа сетей. М., Мир, 1984, – 496 с.

2. Емеличев В. А., Мельников О. И., Сарванов В. И., Тышкевич Р. И. Лекции по теории графов. М., Наука, 1990, – 384 с.

3. Сай В.М., Сизый С.В. Математическая модель региональной планетарной структуры управления железнодорожным транспортом / Организационно-экономические проблемы транспорта в условиях реформирования: Сб. научн.тр.: Фундаментальные и прикладные исследования – транспорту: – Вып. 20 (102). – Екатеринбург: УрГУПС. – 2002. – С. 372-391.

4. Сай В.М. Планетарные структуры управления на железнодорожном транспорте: монография. – М.: ВИНИТИ РАН, 2003. – 345 с.

5. Мальцев А. И. Алгебраические системы. М., Наука, 1970, – 396 с.

6. Общая алгебра. Серия «Справочная математическая библиотека». Под общ. ред. Л. А. Скорнякова. – М.: Наука. 1990. – 592 с.

7. Сай В. М., Фомин В. К. Моделирование системы взаимоотношений железной дороги с хозяйствующими субъектами // Транспорт Урала. 2008. № 4 (19). С. 15–19.

8. Сай В.М., Сизый С.В. Организационные структуры как мультиоператорные сети. Задачи прочности и устойчивости. – Транспорт Урала. 2009. № 2 (21). С. 5–9. ISSN 1815–9400.

9. Сизый С.В. Модель образования и распада организационных сетей в экономико-правовом пространстве. ВИНИТИ РАН: Транспорт, наука, техника, управление. – 2010. – № 3. – С. 16–26.

10. Сизый С. В. Сетевая поддержка предприятий в градуированных организационных сетях. Вестник УрГУПС. Екатеринбург : УрГУПС, 2010. №1. С. 33–45. ISSN 2079-0392.

11. Сай В. М., Сизый С.В. Математическая модель региональной планетарной структуры управления железнодорожным транспортом. В сб. тр. Фундаментальные и прикладные исследования транспорту. МПС РФ, УрГУПС, – Екатеринбург- 2002, вып. 20 (102), – с. 372–391.

12. Сай В. М. Математическая формализация формирования корпоративных структур в экономическом пространстве. Деп. в ВИНИТИ РАН 30.01.03. – № 190. – В2003. – 18 с.

13. Сизый С. В. Траектории развития организационных сетей. Принцип наименьшего действия. ВИНИТИ РАН: Транспорт, наука, техника, управление. – 2010. – № 5. – С. 37–53.

14. Сизый С. В., Сай В. М. Геометрические характеристики организационных сетей. Мир транспорта. 2011. № 1. С. 90-102. ISSN 1992–3252.

15. Сизый С. В. Об определяемости градуированных сетей. Вестник УрГУПС. Екатеринбург : УрГУПС, 2010. № 3(7). С. 28–41. ISSN 2079-0392.

16. Кейслер Г., Чэн Ч. Ч. Теория моделей. М., Мир, 1977. – 614 С.

17. П. Дюндар, А. Айтак, В. Айтак, Вычисление индекса доступности и окрестной целостности графа, Математические заметки, том 78, выпуск 5, 2005, стр. 676-686.

18. Alpay Kırlangı, Graph operations and neighbor-integrity, Mathematica Bohemica, Vol. 129 (2004), No. 3, 245–254.

19. Bagga, K. S.; Beineke, L.W.; Lipman, M. J.; Pippert, R. E.: Edge-integrity: a survey, Discrete Math. 124 (1994), 3–12.

20. Попков В. К, Математические модели связности / Отв. Ред. А. С. Алексеев. – 2-е изд., испр. и доп. – Новосибирск: Изд. ИВМиМГ СО РАН, 2006. – 490 с.

21. Broadbent S.R., Hammersley J.M., Percolation processes, I and II, Proc. Cambridge Philos. Soc., 53 (1957), 629-645.

22. Кестен Х. Теория просачивания для математиков, М. :Мир, 1986.

23. Воробьев В.А., Лаходынова Л.В. О гипотезе замены задачи узлов теории просачивания задачей связей, Автометрия, том 42, №3, 2006, стр 76–85.