Группы геометрических характеристик организационной сети и их интерпретации

Прежде всего, обобщим усредненные геометрические характеристики, предложенные в [12] для планетарных структур, на значительно более широкий класс произвольных градуированных организационных сетей.

Группу усредненных геометрических коэффициентов составляют показатели, отражающие строение исследуемой организационной сети как геометрического объекта, то есть отражающие количество связей между узлами, наличие или отсутствие замкнутых циклов в сети , долю предприятий на уровнях и т. п.

Одним из важных объективных показателей стабильности и независимости отдельного узла, группы узлов, либо целой подсети в сети , является наличие или отсутствие самообеспечения (автаркии) рассматриваемого фрагмента реальной организационной сети .

Наличие самообеспечения предприятий выражается в наличии петель на узлах сети , а самообеспечение группы предприятий, замкнутость производственных циклов – в виде наличия замкнутых циклов в диаграмме сети . Указанные свойства сети можно охарактеризовать с помощью коэффициентов 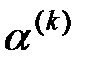автаркии k-ого порядка – отношения имеющегося числа 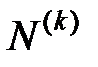циклов длины k в сети к общему максимально возможному числу 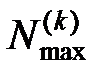циклов длины k в этой сети:

.

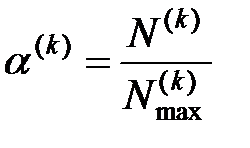Несложно формально подсчитать, что максимальное возможное число различных циклов длины k в сети , содержащей всего N штук узлов, равно

.

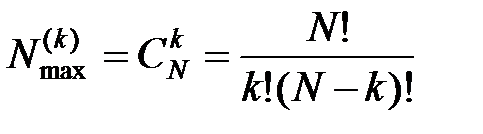В реальных сетях, из-за наличия каких-либо естественных ограничений на возможные связи между предприятиями, это число может быть значительно меньше.

При k = 1 получаем коэффициент автаркии 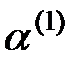первого порядка – отношение имеющегося числа петель на узлах сети к общему числу узлов. Очевидно, при этом, что

,

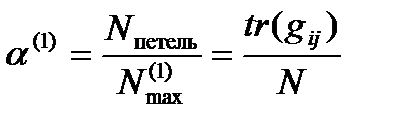где 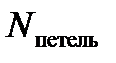– число петель в диаграмме сети ; 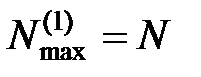– общее число узлов сети ; 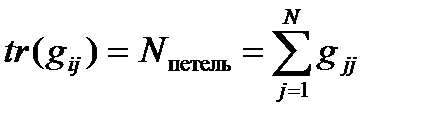– cлед матрицы смежности сети , то есть сумма ее диагональных элементов. Ясно, что для всех коэффициентов автаркии 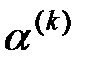выполнено .

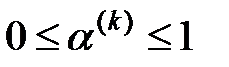Очевидно, что процессы распада сетей [13], процессы разрыва циклов и петель влекут за собой либо абсолютное уменьшение значений коэффициентов автаркии 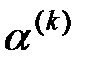, либо уменьшение значений коэффициентов 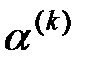для небольших порядков k c незначительным увеличением коэффициентов 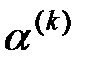более высоких порядков (удлинение технологических и производственных циклов). Это означает уменьшение доли групп самообеспечивающихся предприятий, функционирующих в структуре градуированной сети. Хронологическое изменение коэффициентов автаркии отражает степень самообеспечения, независимости и устойчивости сети (или ее фрагментов) и может служить количественной характеристикой процессов настройки сетевой организационной структуры.

В градуированных организационных сетях процессы формирования предприятий и изменения их ранга – перемещения с уровня на уровень протекают непрерывно [13]. Например, в настоящее время, в процессе реформирования железнодорожного транспорта, в организационной сети ОАО «РЖД» происходит «выделение» предприятий на уровни более низкого ранга. Предприятиям, ранее находившимся в структуре железной дороги, предоставляется большая организационно-правовая самостоятельность, образуются дочерние компании, компания ОАО «РЖД» освобождается от непрофильной деятельности и т.п.

Для отражения этих процессов удобно использовать коэффициенты 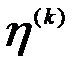наполнения уровней сети : отношение числа узлов на k-ом уровне 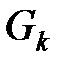к общему числу узлов сети :

,

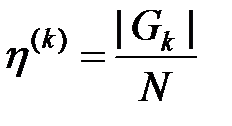где 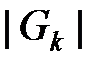– число узлов сети , находящихся на уровне 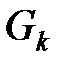ранга k; N – общее число узлов сети .

Поскольку коэффициент 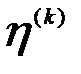реально означает долю предприятий сети , находящихся на уровне ранга k, то очевидно, что:

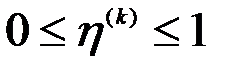и .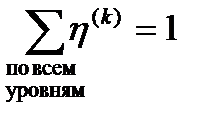

то есть функция 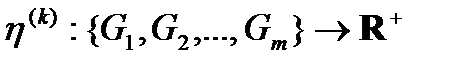являетсяфункцией распределения плотности узлов сети по уровням градуировки.

Введем еще две группы усредненных геометрических коэффициентов градуированной сети – коэффициенты связности уровней. Они характеризуют среднее количество связей узла, расположенного в сети на уровне 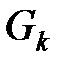ранга k c узлами этого же уровня и с узлами следующего уровня 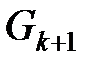большего ранга. Определение и формальные математические выражения этих коэффициентов следующие.

а) Коэффициенты внутриуровневой связности :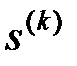

,

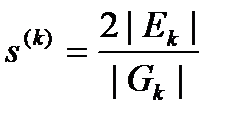где 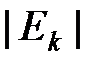– общее число ребер между различными узлами ранга k; 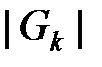– число узлов сети ранга k. Наличие множителя 2 в предлагаемой формуле объясняется тем, что каждому ребру соответствуют в точности два концевых узла, которые этим ребром соединены. Поэтому, при подсчете среднего числа ребер, выходящих из узлов уровня, необходимо формально каждое ребро «разделить пополам» (одна половинка ребра относится к одному узлу – концу ребра, другая – к другому концу ребра) и считать общее количество «половинок» ребер. На рисунке 2.5 изображены примеры фрагментов одного уровня сети и приведены результаты вычисления коэффициентов внутриуровневой связности 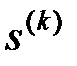для этих фрагментов:

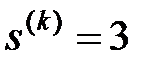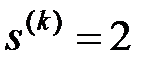а) ; б) ; в)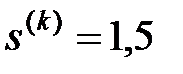

Рис.2.5. Примеры вычисления коэффициентов 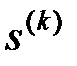(на рисунке изображены только узлы одного ранга k)

Очевидно, что максимальное значение 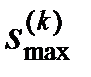коэффициентов внутриуровневой связности равно 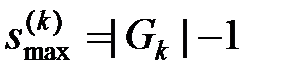, то есть достигается на полном 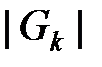-элементном графе 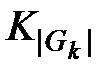, в котором каждый узел связан с каждым [2]. Удаление каких-либо связей между элементами данного уровня влечет уменьшение соответствующего коэффициента внутриуровневой связности 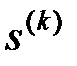. Таким образом, коэффициенты внутриуровневой связности характеризуют степень «монолитности» данного уровня, насыщенность уровня организационными связями, его «прочность» как самостоятельного образования по отношению к возможным внешним воздействиям.

б) Коэффициенты 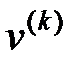связности уровня 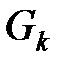с уровнем следующего ранга :

,

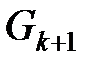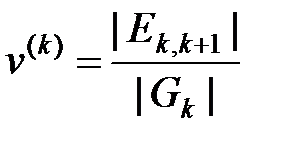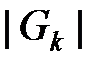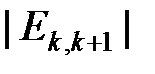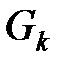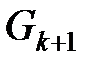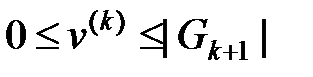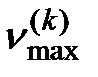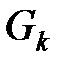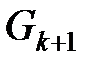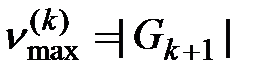где – число узлов сети на уровне ранга k, – общее число ребер, идущих от всех узлов уровня в узлы следующего уровня «более низкого» ранга. Очевидно, что и максимальное значение коэффициентов связности уровня с уровнем следующего ранга равно , то есть достигается на полном двудольном [2] графе 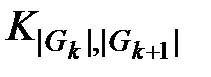, в котором каждый узел уровня 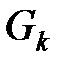связан с каждым узлом уровня .

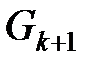Предлагаемые коэффициенты связности соседних уровней характеризуют на геометрическом языке степень «привязанности» уровней организационной сети друг к другу, наполненность организационными связями межуровневого пространства. Эти коэффициенты являются, в некотором смысле, показателями прочности сети и показателями насыщенности процессов взаимодействия между уровнями разных рангов.

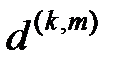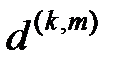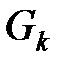Введем еще один геометрический показатель – коэффициент достижимости . Коэффициент достижимости узлов характеризует среднюю длину путей в диаграмме сети от узлов уровня до узлов уровня 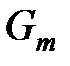. При этом, естественно, не исключается случай равенства рангов k = m. Математическое выражение этого коэффициента таково:

,

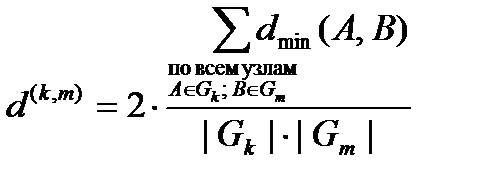где 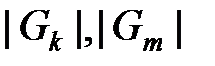– общее число узлов сети рангов k и m соответственно; 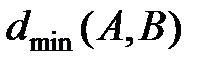– длина минимального пути в сети между узлами А и В.

Сумма в числителе дроби берется по всевозможным парам узлов А и В, рангов, соответственно, k и m. Произведение 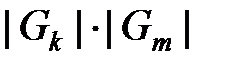в знаменателе есть в точности количество всевозможных пар узлов таких, что первая компонента этой пары имеет ранг k, а вторая – ранг m. Множитель 2 перед дробью мотивируется точно так же, как и при определении коэффициентов внутриуровневой связности.

Ясно, что длина кратчайшего пути от одного узла до другого в сети – важная характеристика организационного устройства сети, отражающая скорость взаимодействия между узлами, скорость влияния и воздействия узла на узел, скорость распространения и передачи информации, директивного или планово-договорного воздействия одного узла на другой.

На рисунке 2.6 приводятся примеры двух сетей, наглядно демонстрирующие принципиальное отличие иерархических организационных структур от планетарных структур управления [4], выражаемое с использованием коэффициента достижимости.

Иерархия Планетарная структура Рис. 2.6. Примеры определения коэффициента достижимости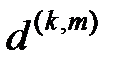

Видно, что в планетарных организационных структурах коэффициенты достижимости значительно меньше, чем в иерархиях. Так, на рисунке 2.6, обе сети содержат 7 узлов, но достижимость узлов А и В (одинакового ранга!) для иерархии 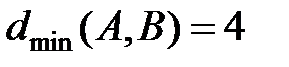, так как все взаимодействия в иерархических структурах осуществляются только через вышестоящие организации. В то же самое время в планетарной структуре связь и взаимодействие между этими же узлами устанавливается (в силу большей экономической и юридической самостоятельности предприятий) напрямую и достижимость становится равной .

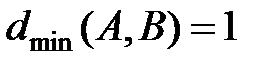Ясно, что все введенные геометрические характеристики градуированной сети теоретически могут быть вычислены на основании её матрицы смежности 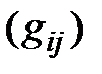с использованием различных стандартных алгоритмов сетевого анализа (поиска в ширину, поиска в глубину, переборного алгоритма маршрутизации). Как было отмечено выше, такое вычисление является трудоемким процессом, требующим значительных вычислительных затрат и больших объемов памяти (в особенности, для больших сетей с большим числом элементов). Кроме того, использование матриц смежности страдает отсутствием наглядности алгоритмических процедур.