Понятие многоосновной мультиоператорной сети

В задачах моделирования и исследования сетевых объектов – транспортных сетей (железнодорожных, автомобильных и т.п.), организационных структур, экономико-правового взаимодействия хозяйствующих субъектов, информационного обмена между объектами и других подобных задачах, связанных с реальной практической деятельностью, в качестве основных моделей, как правило, применяются графы и сети.

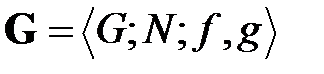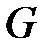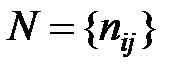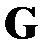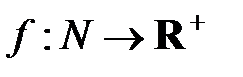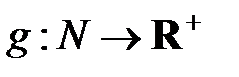Сеть – классическое математическое понятие дискретной математики, выделившееся в отдельный раздел изучения из классической теории графов [1, 2]. Традиционно, в работах по дискретной математике, сетью называют ориентированный граф с помеченными ребрами , где – множество вершин графа (обычно занумерованных натуральными числами), – множество ребер графа ; и – функции меток ребер графа 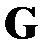, присваивающие каждому ребру 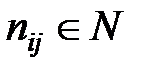, соединяющему вершины 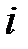и , некоторую пару неотрицательных чисел 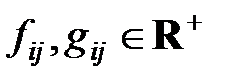, называемых «потоком» (величина 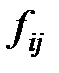) и «пропускной способностью» (величина 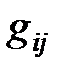) ребра 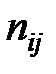[1, 2]. При этом, в зависимости от рассматриваемой задачи, на сеть 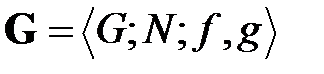дополнительно налагаются различные естественные условия, например:

1) 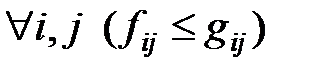– поток в каждом ребре не превосходит пропускной способности этого ребра;

2) 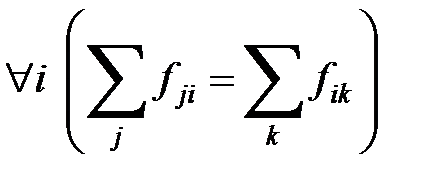– условие сохранения потока в узле, означающее, что для любого узла 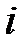, сумма всех потоков в него входящих, равняется сумме всех потоков, выходящих из этого же узла.

(50, 50)

(70, 40)

(30, 50)

(50,50)

(20, 20)

(40, 60)

(30, 50)

(70, 70)

(50, 60)

(20, 30)

Рис. 2.1. Пример сети

В дискретной математике сети традиционно изображаются в виде ориентированных графов с помеченными ребрами, при этом меткой каждого ребра 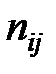служит соответствующая этому ребру пара чисел «поток – пропускная способность» (рис. 2.1).

Таково формальное классическое понятие сети, повсеместно применяемое при моделировании и проектировании реальных сетевых структур.

Однако практический опыт моделирования реальных объектов показал, что классические понятия графов и сетей, как правило, приходится значительно расширять и детализировать, чтобы отразить в них многие дополнительные свойства и параметры рассматриваемых объектов. Так при моделировании реальных объектов, ребра возникающих сетей, как правило, приходится помечать не одним потоком 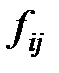, а несколькими различными по смыслу потоками, соответствующими различным по своей природе параметрам взаимодействия между узлами – транспортные ресурсные, финансовые, информационные и другие потоки. Кроме того, зачастую, в моделях возникают различного рода разбиения сетей на фрагменты, а также разнообразные раскраски узлов сети и ее ребер. Очевидно, что дополнительные потоки, разбиения сетей и их раскраска являются, с математической точки зрения, расширением и пополнением [5] стандартной сигнатуры 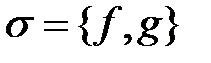исходной алгебраической структуры «сеть ».

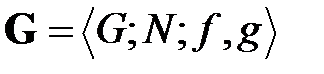Анализ результатов моделирования сетей реальных объектов [3, 4] приводит к пониманию необходимости формирования нового математического понятия – сетей с расширенной сигнатурой, которые в дальнейшем будем называть многоосновные мультиоператорные сети. Многоосновные мультиоператорные сети являются универсальным обобщением классических понятий сетей и графов, их возникновение инициировано практической деятельностью – моделированием и интерпретацией реальных организационных и транспортных сетей.

Многоосновная мультиоператорная сеть – это многоосновная алгебраическая система (модель) 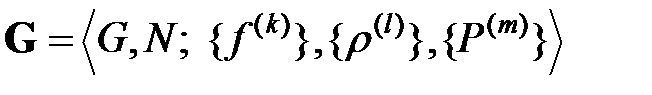[5]. Здесь 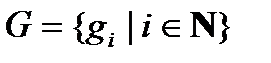– множество вершин (обычно нумерованное натуральными числами 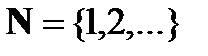); 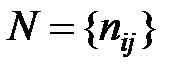– множество ребер (ребро 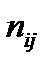соединяет вершины 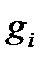и 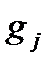). Сигнатура многоосновной мультиоператорной сети 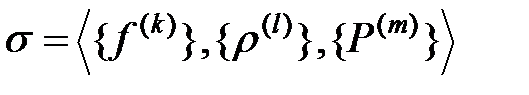состоит из:

А) некоторого количества бинарных отношений эквивалентности 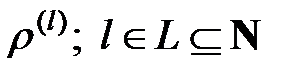, являющихся различными разбиениями основных множеств вершин 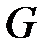и ребер 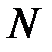на классы «однотипных» элементов по какому-то выделенному в рассмотрение признаку;

Б) некоторого количества числовых функций вида 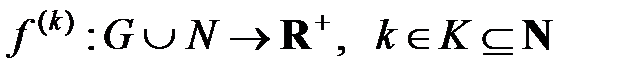, представляющих различные метки (потоки и характеристики) вершин и ребер сети ;

В) некоторого количества операторов

,

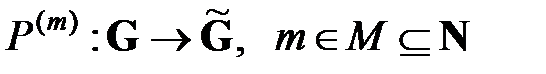которые воздействуют на сеть 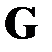, изменяя ее вершины, ребра и метки (величины потоков) в соответствии с различными «внешними» воздействиями на моделируемую сетевую организационную структуру, трансформируя, таким образом, исходную сеть 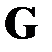в некоторую новую сеть .

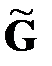В многоосновных мультиоператорных сетях, возникающих при моделировании реальных сетей, сигнатурные разбиения 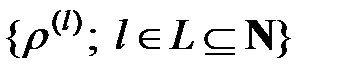сети , как правило, отражают разделение субъектов хозяйственной деятельности на всевозможные типы, например, сектора и группы по видам производимой продукции, по значимости и рангу, по экономической состоятельности и устойчивости и т.п. Метки 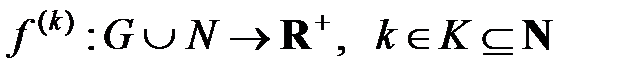узлов и ребер мультиоператорной сети , как правило, отражают количественные показатели рассматриваемых субъектов – финансовые и ресурсные потоки, объемы производимой продукции или оказанных услуг, численные показатели и характеристики хозяйственной деятельности предприятий и т.п. Операторы 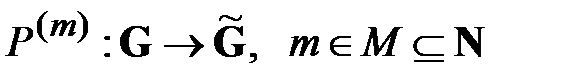сети , как правило, формализуют различные внешние воздействия на сеть, случайные стохастические изменения, форс-мажорные обстоятельства, директивные преобразования сети, закрытие и удаление узлов, ребер, изменения потоков и связей, изменения в потребностях ресурсов и т.п.

Многоосновную мультиоператорную сеть можно, при необходимости, интерпретировать как совокупность графа и некоторого количества реляционных баз данных, в которых сигнатурные отношения и функции 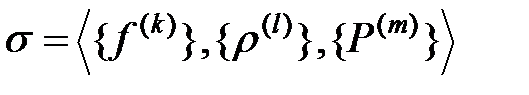(то есть вся информация о моделируемых предприятиях и связях между ними, а так же рассматриваемые параметры и внешние воздействия, учитываемые при моделировании) хранятся в виде электронных таблиц – значений сигнатурных отношений, функций и операторов. Взгляд на мультиоператорные сети как на вариант достаточно традиционных и широко применяемых реляционных баз данных становится особенно полезным при представлении этих сетей в электронном виде, последующем их компьютерном анализе, хранении и обработке.