Вопрос №15. Отношение «равно», «меньше» И «больше» на мно-во N0

Равномощность означает равночисленность а=в <-> А ~В

Отношения равенства обладает свойствами рефлективности, симметричности и транзитивности, значит яв-ся отношением эквивалентности. Пусть А не ~ , это значит А и В пренадлежат разным классам эквивалентности и А не равно В

Если мн-во А равномощно некоторому подмножеству В1 мн-ва В , то говорят что число а1 меньше числа В ( А меньше В)

(a<b) ó A~B1, где B1<B и B1 не равно пустому множеству, В 1 не равно В

Если А меньше В , то говорят так же , что В больше А и записывают B>A
Отношение меньше обладает след свойствами :

Вопрос №16.Сумма и разность целых неотрицательных чисел.

Суммой целых неотриц. чисел а и в наз-ся число а+в=m(АᴗВ), где а=m(А), в=m(В), А∩В=

Теорема. Сумма любых 2-х целых неотриц. чисел существует и она единственна.

Свойства сложения:

1)для любых а,в 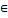N₀ (а+в=в+а)-коммутативный закон (это следует из из свойства множеств АᴗВ=ВᴗА)

2)для любых а,в,с 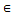N₀ ((а+в)+с=а+(в+с))-ассоциативный закон. Сумма трех чисел определяется по формуле: а₁+а₂+а₃=(а₁+а₂)+а₃

Разностью целых неотриц. чисел а и в наз-ся число а - в, к-ое определяется по формуле (а-в)=m(А\В), где а=m(А), в=m(В), В с А

Теорема. Разность чисел а и в 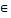N₀ существует и единственно тогда и только тогда, когда в≤а.

Вопрос №17. Произведение и частное целых неотрицательных чисел.

1.Произведением чисел a и b из N₀ называется число a • b удовлетворяющее условиям:

1) a•b= a+a+a+…+a; при b>1; b слагаемых

2) a•1=a; при b=1;

3) a•0=0; при b=0;

2.Произведением чисел a и b из N₀ называется число a•b равное числу элементов в декартовом произведении множества АxВ; таких что a•b=m(AxB),где a=m(A); b=m(B).

Теор. Произведение любых 2-х целых неотрицательных чисел существует и оно единственно.

Операция умножения коммутативна, ассоциативно, дистрибутивно относительно вычитания.

Деление целого неотрицательного числа на натуральное связано с разбиением множества на классы . Рассмотрим мн-во A, такое что m(A)=a. Пусть мн-во Aразбита на попарно непересекающиеся равночисленные классы или подмножества, тогда

1) если b= число подмножеств в разбиении, то частным a:b – это численность каждого подмножества.

2) Если b- численность каждого подмножества, то частным a:b называется число подмножеств в разбиении.

Число a-делимым;b-делителем.

Вопрос №18. Множество комплексных чисел.

Уравнение (x² +1 = 0) - не имеет действительных корней.

Выражение ( √-4 ) - не имеет смысла на множестве действительных чисел.

Для их решения6

Комплексные числа – числа вида z=a+b*i

a, b – действительные числа

i – мнимая единица (i² = -1)

Действительная часть комплексного числа - число a (a=ReZ) – от слова “Real”).

Мнимая часть комплексного числа – число b (b=ImZ) – от слова “Image”).

Если a=0 ð (z=b*i) – чисто мнимое число.

Если b=0 ð (z=a) - обычное действительное число.

Множество действительных чисел R – подмножество множества комплексных чисел (C)

RcC (R входит в C)

Степени числа I:

i²= -1

i³= i * i² = I * (-1) = - i

i⁴= (i²)² = (-1)² = 1

i⁵= i * i⁴ = i * 1 = i

Равные комплексные числа

- два комплексных числа Z₁ = a₁ + b₁ * i

Z₂ = a₂ + b₂ * i

A₁ = a₂ ;b₁ = b₂