Численные методы решения системы линейных уравнений
Постановка задачи
Дана система линейных уравнений:
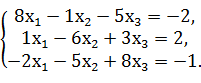
Требуется решить систему уравнений, используя:
• метод Гаусса (решение в обыкновенных дробях);
• метод простой итерации (3 итерации);
• метод Зейделя (3 итерации).
Метод Гаусса
1. Прямой ход метода Гаусса:
Запишем систему в виде матрицы, включив коэффициенты уравнений и свободные члены:
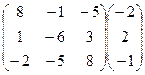
Работаем со столбцом №1
Умножим 1-ую строку на (1/8) и добавим к 3-ей:
| -0,125 | -0,625 | -0,25 | |
| -5,875 | 3,625 | 2,25 | |
| -5,25 | 6,75 | -1,5 |
Работаем со столбцом №2
Умножим 2-ую строку на (-5,875) и добавим ко 3-ой:
| -0,125 | -0,625 | -0,25 | |
| -0,617 | -0,383 | ||
| 3,5106 | -3,5106 |
Умножим 3-ую строку на (3,5106):
| -0,125 | -0,625 | -0,25 | |
| -0,617 | -0,383 | ||
| -1 |
Получим единицы на главной диагонали. Для этого всю строку делим на соответствующий элемент главной диагонали:
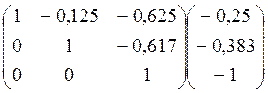
Теперь исходную систему можно записать как:
x1 = -0,25- ( - 0,125x2 – 0,625x3)
x2 = -0,383 - ( - 0,617x3)
x3 = -1
2. Обратный ход метода Гаусса:
Из 3-ой строки выражаем x3
Из 2-ой строки выражаем x2
x2 = -1
Из 1-ой строки выражаем x1
x2 = -1
Получили ответ: (-1,-1,-1).
Метод простой итерации
Проверим условие сходимости: Для сходимости метода необходимо и достаточно, чтобы в матрице A абсолютные значения всех диагональных элементов были больше суммы модулей всех остальных элементов в соответствующей строке.
Наша система имеет вид:
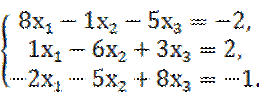
|8|>|-1|+|-5|-да
|-6|>|1|+|3|-да
|8|>|-2|+|-6|-да
Условие сходимости выполняется.
Выберем начальное приближение: 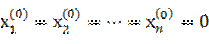
Для организации итерационного процесса запишем систему в приведенном виде:
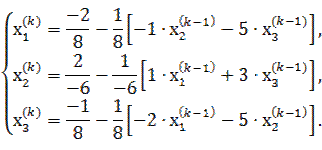
Получим:
x1=-0,25-0,125x2-0,625x3
x2=-0,33-0,17x1-0,5x3
x3=-0,125+0,25x1-0,625x2
Проведем три итерации:
1 итерация:
x1 = -0,25
x2 = -0,333333333
x3 = -0,125
2 итерация:
x1 = -0,369791667
x2 = -0,4375
x3 = -0,395833333
3 итерация:
x1 = -0,552083333
x2 = -0,592881944
x3 = -0,490885417
Результат после выполнения трех итераций: (-0,552;-0,593;-0,491).
Метод Зейделя
Наша система имеет вид:
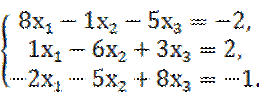
Для организации итерационного процесса запишем систему в приведенном виде:
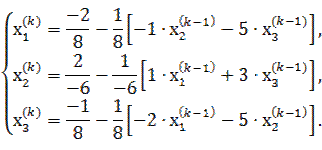
Получим:
x1=-0,25-0,125x2-0,625x3
x2=-0,33-0,17x1-0,5x3
x3=-0,125-0,25x1-0,625x2
Проведем три итерации:
1 итерация:
x1 = -0,25
x2 = -0,375
x3 = -0,625
2 итерация:
x1 = -0,6875
x2 = -0,760416667
x3 = -0,772135417
3 итерация:
x1 = -0,827636719
x2 = -0,857340495
x3 = -0,867746989
Результат после выполнения трех итераций:
(-0,828;-0,857;-0,868).
Численные методы решения задачи аппроксимации
Постановка задачи
| x | -3 | -1 | |||
| f(x) | -3 | -2 |
Требуется:
• решить задачу интерполяции методом неопределенных коэффициентов (кусочно-линейная для каждой последовательной пары точек 1+2, 2+3, 3+4, 4+5, кусочно-параболическая интерполяция для каждой последовательной тройки точек 1+2+3, 3+4+5)
• решить задачу интерполяции с использованием полинома Лагранжа(кусочно-линейная для каждой последовательной пары точек 1+2,2+3,3+4,4+5, кусочно-параболическая интерполяция для каждой последовательной тройки точек 1+2+3, 3+4+5)
• решить задачу аппроксимации полиномом 1-й и 2-й степени методом наименьших квадратов для всех точек 1+2+3+4+5
Решение задачи интерполяции (полиномы первой и второй степени) методом неопределенных коэффициентов
В случае интерполяции функция проходит строго через экспериментальные точки. Для кусочно-линейной интерполяции получим две системы из условия прохождения соответствующей прямой через точки 1+ 2, 2+3, 3+4, 4+5:
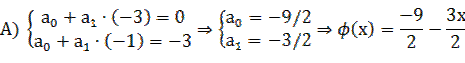
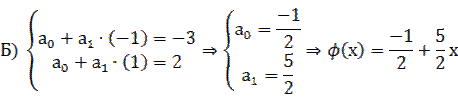
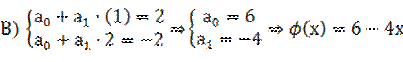
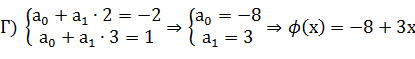
Для квадратичной интерполяции с помощью метода неопределенных коэффициентов получим следующие системы.
Для точек 1+2+3:
| x | -3 | -1 | |
| f(x) | -3 |
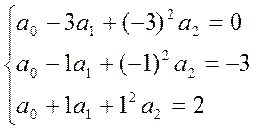
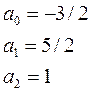
y=5/2x+1x2-3/2
Для точек 3+4+5:
| x | |||
| f(x) | -2 |
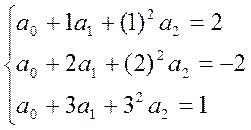
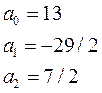
y=-29/2x+7/2x2-13
