Методы решения системы линейных уравнений
1. Правило Крамера. Оно применяется в случае, когда m = n и когда определитель матрицы системы отличен от нуля.
Теорема. Если определитель матрицы системы отличен от нуля, то система совместна и имеет единственное решение:
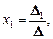
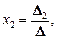 …,
…, 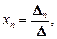 (8)
(8)
где 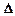 — определитель матрицы системы, а
— определитель матрицы системы, а 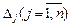 — вспомогательные определители, полученные из
— вспомогательные определители, полученные из 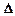 заменой j-го столбца столбцом свободных членов.
заменой j-го столбца столбцом свободных членов.
Пример. Решить систему уравнений 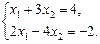
Решение. Находим определитель 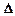 данной системы:
данной системы:
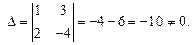 Система совместна. Имеем:
Система совместна. Имеем:
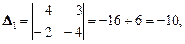
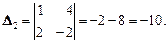
Следовательно, 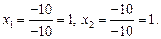
Ответ: 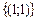 .
.
2. Метод обратной матрицы.Он также применяется в случае, когда m = n и 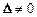 . Систему
. Систему
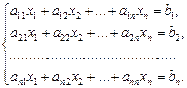 (9)
(9)
можно записать в матричном виде А · Х = В, где
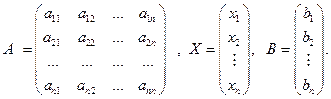
Умножив обе части уравнения слева на А–1, получим
X = A–1 · B. (10)
Пример. Решить систему уравнений 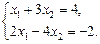
Решение. Из решения рассмотренного ранее примера,
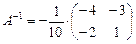 .
.
Тогда по формуле (10) получим: X = A–1 · B = 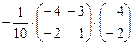 =
=
= 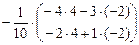 =
= 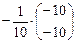 =
= 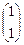 .
.
Ответ: 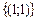 .
.
3. Метод Гаусса(метод исключения неизвестных). Он применяется для решения системы (7) в произвольном случае.
Преобразования, аналогичные элементарным преобразованиям над строками расширенной матрицы системы (7), будем называть элементарными преобразованиями этой системы. К ним отнесем еще удаление из системы уравнений типа 0 = 0.
В случае совместности системы (7) она может быть приведена при помощи элементарных преобразований к виду
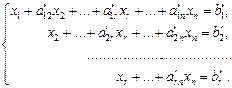 (11)
(11)
Очевидно, число r равно рангу матрицы системы (который в случае совместности системы совпадает с рангом расширенной матрицы). Это число называется рангом системы. Очевидно, что r 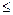 n.
n.
Если r = n, тогда система имеет единственное решение.
Пример. Решить систему уравнений 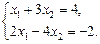
Решение. Из второго уравнения системы вычитаем первое, умноженное на 2. Получаем 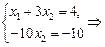
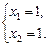
Ответ: 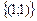 .
.
Если r 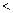 n, то система (7) в этом случае имеет бесконечное множество решений.
n, то система (7) в этом случае имеет бесконечное множество решений.
Систему (11) запишем в виде
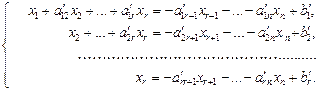 (12)
(12)
Неизвестным xr+1,…, xn присваиваются любые значения, и поэтому они называются свободными. Неизвестные x1, x2,…, xr называются базисными. Двигаясь снизу вверх, находим значения всех неизвестных 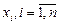 .
.
Вопросы для самопроверки
1. Что называется n-мерным арифметическим пространством?
2. Что называется скалярным произведением двух векторов?
3. Какие системы векторов называются линейно независимыми?
4. Что называется базисом пространства Rn?
5. Что называется матрицей? Как определяются действия над матрицами?
6. Каково правило вычисления определителей второго и третьего порядков?
7. Как вводится понятие определителя в общем случае?
8. Как вводятся минор и алгебраические дополнения к элементу aij?
9. Какая матрица называется обратной по отношению к данной? Всегда ли к данной матрице существует обратная?
10. Каково правило нахождения обратной матрицы?
11. Как найти ранг матрицы?
12. Какая система линейных уравнений называется совместной? Каковы необходимое и достаточное условия совместности системы?
13. Какие существуют методы решения системы линейных уравнений? В чем их суть?
14. В каком случае система линейных уравнений имеет единственное решение, бесконечное множество решений?
Типовая задача 3
Даны векторы 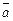 = (2;–1;3),
= (2;–1;3), 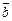 = (1;2;–3),
= (1;2;–3), 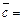 (0;1;2),
(0;1;2), 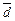 = (–1;9;–13)
= (–1;9;–13)
со своими координатами в базисе 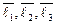 . Показать, что векторы
. Показать, что векторы 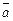 ,
, 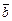 ,
, 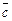 сами образуют базис, и найти разложение вектора
сами образуют базис, и найти разложение вектора 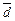 в новом базисе.
в новом базисе.
Решение. Вычисляем определитель, составленный из координат этих векторов: 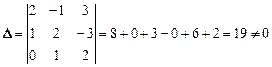 .
.
По теореме 1, сформулированной выше, векторы 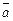 ,
, 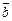 ,
, 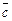 образуют базис пространства R3.
образуют базис пространства R3.
Пусть 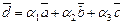 — разложение вектора
— разложение вектора 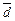 по базису
по базису 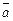 ,
, 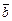 ,
, 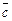 .
.
По условию задачи имеем:
–1· 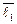 + 9 ·
+ 9 · 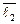 – 13 ·
– 13 · 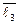 =
= 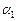 · (2 ·
· (2 · 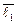 – 1 ·
– 1 · 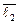 + 3·
+ 3· 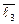 ) +
) +
+ 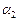 · (1 ·
· (1 · 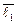 + 2 ·
+ 2 · 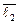 – 3 ·
– 3 · 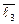 ) +
) + 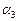 · (0 ·
· (0 · 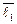 + 1 ·
+ 1 · 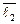 + 2·
+ 2· 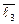 ),
),
–1· 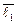 + 9 ·
+ 9 · 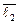 – 13 ·
– 13 · 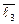 = (2 ·
= (2 · 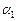 + 1 ·
+ 1 · 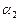 + 0 ·
+ 0 · 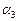 ) ·
) · 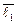 +
+
+ (–1 · 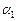 + 2 ·
+ 2 · 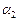 + 1 ·
+ 1 · 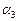 ) ·
) · 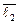 + (3 ·
+ (3 · 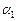 – 3 ·
– 3 · 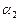 + 2 ·
+ 2 · 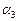 ) ·
) · 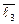 .
.
Из условия равенства двух векторов получим:
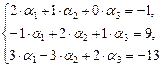
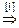
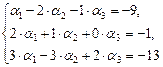
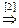

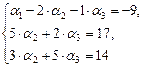
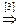
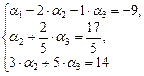
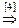
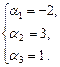
[1]: Обе части второго уравнения умножим на (–1). Поменяем местами первое и второе уравнения.
[2]: Обе части первого уравнения умножим на (–2) и прибавим соответственно ко второму уравнению. Затем обе части первого уравнения умножим на (–3) и прибавим соответственно к третьему уравнению.
[3]: Обе части второго уравнения разделим на 5.
[4]: Обе части второго уравнения умножим на (–3) и прибавим соответственно к третьему уравнению. Из третьего уравнения системы 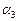 = 1. Подставим это значение во второе уравнение и получим
= 1. Подставим это значение во второе уравнение и получим 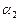 = 3. Подставляя полученные значения
= 3. Подставляя полученные значения 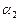 = 3,
= 3, 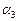 = 1 в первое уравнение, найдем
= 1 в первое уравнение, найдем 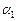 = –2.
= –2.
Итак, 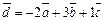 .
.
Ответ: 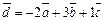 .
.
Типовая задача 4
Исследовать на совместность и решить систему уравнений
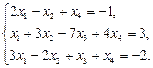
Решение. Находим ранги матрицы системы и расширенной матрицы:
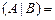
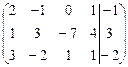
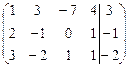
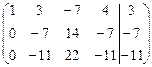
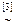
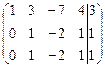
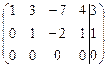 .
.
[1]: Меняем местами первую и вторую строки.
[2]: Элементы первой строки умножим на (–2) и прибавим соответственно к элементам второй строки. Затем элементы первой строки умножим на (–3) и прибавим соответственно к элементам третьей строки.
[3]: Элементы первой строки разделим на (–7), а элементы второй строки — на (–11).
[4]: Из элементов второй строки вычтем элементы третьей строки.
Итак, 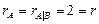 .
.
По теореме Кронекера-Капелли система совместна.
Так как 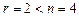 , то система имеет бесконечное множество решений.
, то система имеет бесконечное множество решений.
При помощи элементарных преобразований над уравнениями системы, аналогичных приведенным элементарным преобразованиям над строками матрицы, данная система приводится к виду
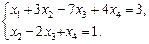
Перенеся члены со свободными неизвестными в правые части системы, получим: 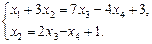
Давая свободным неизвестным х3, х4 произвольные значения t1, t2, получим общее решение системы: 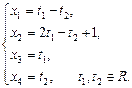
Ответ: 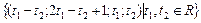 .
.
3. Задание 5
по теме «Теория пределов»
Краткие теоретические сведения
