Дифференциальные уравнения в обобщенных координатах.
Функцией каких аргументов является вектор скорости точки, принадлежащей механической системе с 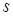 степенями свободы?
степенями свободы?
В случае стационарных связей вектор скорости точки является функцией обобщенных скоростей и обобщенных координат
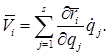
Чему равна частная производная от вектора скорости точки системы по какой-либо обобщенной скорости?
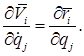
Функцией каких аргументов является кинетическая энергия системы, подчиненной голономным нестационарным связям?
Кинетическая энергия в случае голономных нестационарных связей является функцией обобщенных координат, обобщенных скоростей и времени:
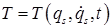 .
.
Какой вид имеют уравнения Лагранжа второго рода? Чему равно число этих уравнений для каждой механической системы?
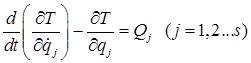 .
.
Число уравнений Лагранжа второго рода равно числу степеней свободы.
Какой вид принимают уравнения Лагранжа второго рода в случае, когда на систему действуют одновременно консервативные и неконсервативные силы?
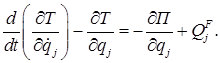
Что представляет собой функция Лагранжа, или кинетический потенциал?
Кинетический потенциал является функцией обобщенных координат, обобщенных скоростей и времени.
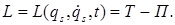
Какой вид имеют уравнения Лагранжа второго рода для консервативной системы?
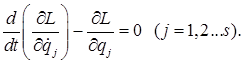
В зависимости от каких переменных величин должна быть выражена кинетическая энергия механической системы при составлении уравнений Лагранжа?
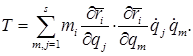
Как определяется потенциальная энергия механической системы, находящейся под действием сил упругости?
Потенциальная энергия механической системы, находящейся под действием сил упругости:
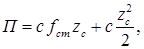
где 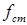 – статическое удлинение пружины;
– статическое удлинение пружины;
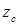 – отклонение центра масс от положения покоя.
– отклонение центра масс от положения покоя.
Какие обобщенные координаты называют циклическими и какой вид имеют циклические интегралы?
Обобщенные координаты, которые не входят явно в выражение кинетического потенциала 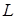 , называются циклическими координатами. Так, например, если тяжелая материальная точка массы m движется в пространстве, то при отсутствии сопротивления координаты x и y являются циклическими.
, называются циклическими координатами. Так, например, если тяжелая материальная точка массы m движется в пространстве, то при отсутствии сопротивления координаты x и y являются циклическими.
Равенства 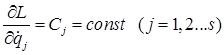 называются циклическими интегралами.
называются циклическими интегралами.
При решении каких задач динамики голономных систем целесообразно использовать уравнения Нильсена?
Уравнения вида
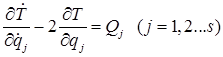
называются уравнениями Нильсена.
Уравнения Нильсена целесообразно использовать при решении задач, связанных с расчетом систем, имеющих большое число степеней свободы.
Каково выражение кинетической энергии механической системы со стационарными связями?
Кинетическая энергия механической системы со стационарными связями является квадратичной формой обобщенных скоростей:
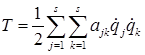 .
.
Каково выражение кинетического потенциала механической системы со стационарными связями?
В случае стационарных связей
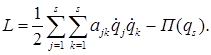
Динамика твердого тела.
