Метод касательных. Скорость сходимости. Критерий окончания

Метод касательных (метод Ньютона).Выбирается точка x₀Î[a,b] и в ней проводится касательная к графику функции y=f(x) и за новое приближение x₁ принимается точка, в которой касательная пересекает ось OX и т.д. В итоге получаем итерационную формулу Ньютона:

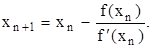(2.6)

Необходимым и достаточным условием сходимости метода Ньютона на отрезке локализации xÎ[a,b] являются:

f¢(x)¹0, - (необходимое условие); (2.7)

f¢¢(x)¹0 - (достаточное условие);

т.е. знакопостоянство первой и второй производной на отрезке локализации.

Критерий окончанияметодов Ньютона:

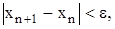
Все методы Ньютона (касательных, хорд и секущих) имеют квадратичную сходимость.

Обусловленность задачи численного интегрирования

Относительное число обусловленности задачи численного интегрирования

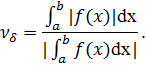
Экзаменационный билет № 24

Требования к вычислительным программам

Требования к программным реализациям алгоритмов

1. Надежность(без ошибок)

2. Работоспособность

3. Переносимость

4. Поддерживаемость

5. Простота

Модификации метода Ньютона для решения нелинейных уравнений

Метод хорд (модификация метода Ньютона).На отрезке [a,b] производную касательную в формуле (2.6) заменяют приближенным равенством:

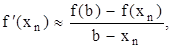
т.е. хордой. В итоге получаем:

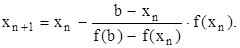(2.8)

Метод секущих (модификация метода Ньютона). Если теперь точку b в формуле (2.8) заменить на точку x_n-1, то получим формулу метода секущих:

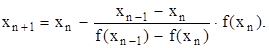(2.9)

Метод секущих является двух этапным.

Все методы Ньютона (касательных, хорд и секущих) имеют квадратичную сходимость.

Критерий окончанияметодов Ньютона:

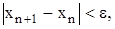
Относительное число обусловленности системы линейных алгебраических уравнений . Влияние значения определителя на погрешность решения системы уравнений

Экзаменационный билет № 25

Метод ячеек

Пусть требуется вычислить двукратный интеграл в области G(a£x£b, c£y£d):

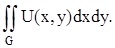
С помощью узлов x_i (i=0,1,..n) и y_j (j=0,1,...,m) и прямых, проходящих через эти узлы: x=x_i и y=y_j, разобьем область G на (n×m) прямоугольных ячеек, имеющих площадь:

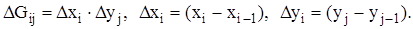
Выбираем в этой ячейке центральную точку:

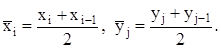
Будем считать, что интеграл для каждой ячейке приближенно равен:

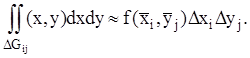(2.12)

Суммируя по всем ячейкам имеем:

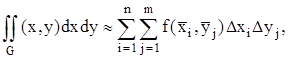(2.13)

при этом погрешность, когда все ячейки имеют одинаковую площадь 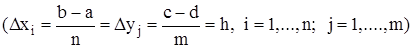будет равна

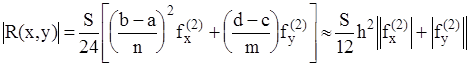; (2.14)

где S - площадь области G, m и n - количество узлов по координатам x,y; 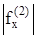, 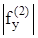- максимальное значение вторых частных производных по соответствующим координатам.

Системы нелинейных уравнений. Метод простой итерации. Метод Ньютона

Версия

Метод простой итерации.Уравнение f(x)=0 преобразуют к виду удобному для организации итерации: x=j(x), при этом функция j(x) называется итерационной функцией. На отрезке локализации [a,b] выбирается начальное приближение x=x₀ и вычисляется x₁=j(x₀). Продолжая этот процесс имеем:

.

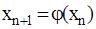Если существует 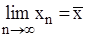, то получаем равенство: 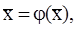где 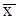- корень. Метод сходится при 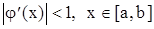, а при 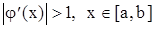- расходится.

Критерий окончания:

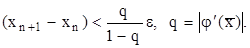
Метод касательных (метод Ньютона).Выбирается точка x₀Î[a,b] и в ней проводится касательная к графику функции y=f(x) и за новое приближение x₁ принимается точка, в которой касательная пересекает ось OX и т.д. В итоге получаем итерационную формулу Ньютона:

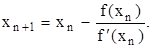(2.6)

Необходимым и достаточным условием сходимости метода Ньютона на отрезке локализации xÎ[a,b] являются:

f¢(x)¹0, - (необходимое условие); (2.7)

f¢¢(x)¹0 - (достаточное условие);

т.е. знакопостоянство первой и второй производной на отрезке локализации.

Версия

Пусть имеется следующая система нелинейных уравнений:

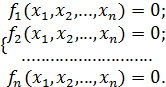(6.5)

Как уже отмечалось выше, для одной переменной метод Ньютона использует замену искомого уравнения уравнением прямой или, как еще говорят, производит линеаризацию исходного уравнения. Пусть имеется k - ое приближение: 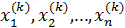. Разложим левые части системы уравнений в ряд Тейлора и учтем только линейные члены:

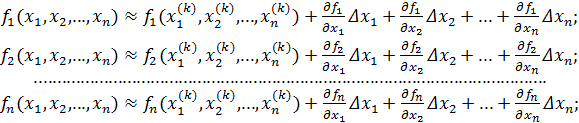(6.6)

где 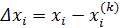, i=1,2,...,n; а частные производные вычисляются в точке k-го приближения: x₁=x₁^(k), x₂=x₂^(k),...,x_n=x_n^(k).

Заменим в исходной системе нелинейные функции f_i(x₁,x₂,...,x_n) на правые части этих приближенных равенств, которые являются линейными функциями относительно переменных x_i, i=1,2,...,n. В итоге получим следующую систему линейных уравнений относительно переменных x_i, i=1,2,...,n:

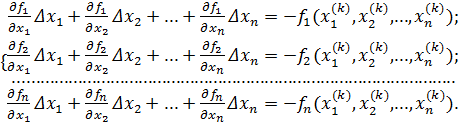(6.7)

Из этой системы можно определить значения x_i, i=1,2,...,n и вычислить значения k+1-приближения: 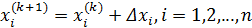. Данная система уравнений представляют собой метод Ньютона для системы нелинейных уравнений.

Определитель этой системы называетсяякобианом.

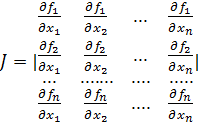. (6.8)

Для существования решения якобиан должен быть отличен от нуля для каждого шага итерации.

Критерий окончания. Итерационный процесс продолжается до тех пор, пока не выполнятся условия: 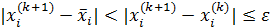, для всех i=1,2,...,n.