Математическое моделирование. Основные этапы математического моделирования

Математическое моделирование. Основные этапы математического моделирования

Математическое моделирование – предмет исследования объектов и явлений окружающего наш мир с помощью их приближенного описания на языке математики – математических моделей.

Процессы математического моделирования:

1. Построение модели

2. Постановка, исследование, решение математической задачи

3. Проверка модели на графике

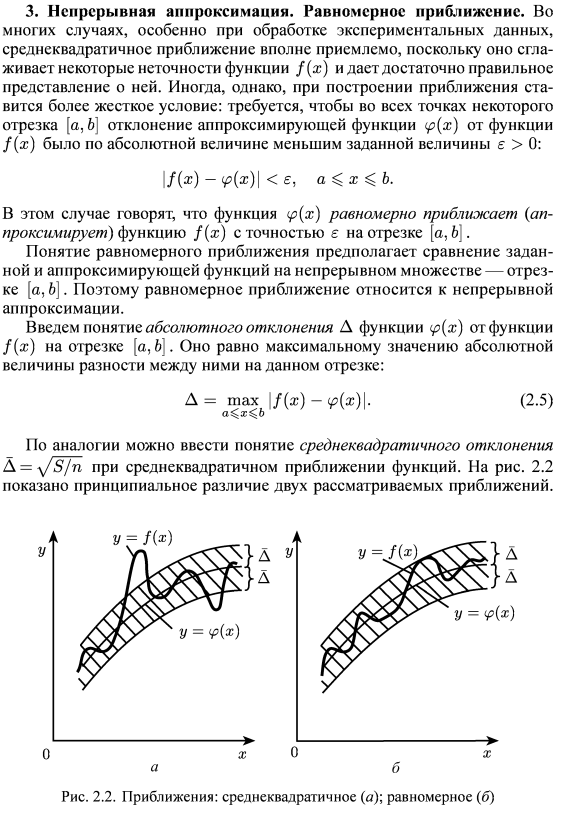
Аппроксимация производных в крайних точках. Аппроксимация частных производных

Аппроксимацию производных конечными разностями в общем случае можно рассматривать как замену производной от функции y¢=f¢(x) производной от аппроксимирующей функции j¢(x), j(x)»f(x), где в качестве аппроксимирующей функции используется интерполяционный многочлен: 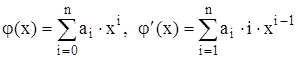. Поэтому увеличивая степень интерполяционного многочлена n мы будем увеличивать порядок точности аппроксимации производной.

С помощью интерполяционного многочлена Лагранжа при равномерном распределении узлов были получены следующие формулы для аппроксимации производной с помощью центральных разностей второго и четвертого порядка точности:

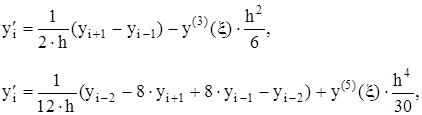(2.8)

где, y^(k)(x) - значение “к”-той производной в некоторой точке на отрезке [x_i-2,x_i+2].

В крайних точках таблицы или в крайних узлах нельзя использовать соотношения для центральных разностей (2.8). В этих точках используются односторонние формулы численного дифференцирования:

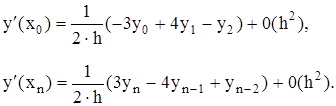
Метод оптимального пассивного поиска минимума функции

На отрезке [a,b] задается последовательность точек x₀,x₁,...,x_n, таких, что x_k=x₀+kh, k=1,...,n; x₀=a, x_n=b. В этих точках вычисляется значение функции f(x_k). За точку минимума 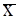принимается та точка x_k, для которой выполняется соотношение: .

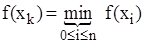Следовательно: 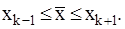Отсюда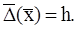

Экзаменационный билет № 2

Погрешности арифметических операций. Правила оценки погрешности.

Погрешности функций

Погрешности арифметических операций:

а) при сложении и вычитании двух величин их абсолютные предельные погрешности складываются:

.

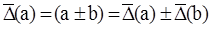б) при умножении и делении двух величин друг на друга их относительные предельные погрешности складываются:

,

.

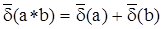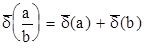в) при возведении в степень приближенной величины ее относительная предельная погрешность умножается на показатель степени:

.

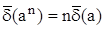Погрешности функций:

Пусть а-приближенное значение аргумента x функции y=f(x), а Dа- абсолютная погрешность аргумента, т.е. 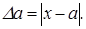При Dа<<1 для оценки абсолютной погрешности и относительной погрешностей функции используются следующие определение/

Абсолютной погрешностью функции Dy называется произведение модуля производной функции на абсолютную погрешность аргумента, а относительной погрешностью функции dy называется отношение абсолютной погрешности функции к ее абсолютному значению, т.е.

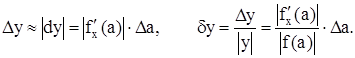
Аналогичные соотношения можно записать для функции нескольких переменных, например, если U=f(x,y,z), то при:

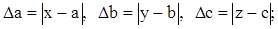
имеет:

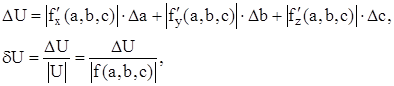
где 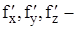частные производные, по соответствующим аргументам.

Полиномы Лежандра

Экзаменационный билет № 7

Требования, предъявляемые к вычислительным алгоритмам. Требования к программным реализациям вычислительной задачи

Требования к вычислительным алгоритмам

1. Экономичность(число элементарных операций)

2. Надлежащая точность(решение задачи с заданной или приемлемой точностью)

3. Экономия памяти(-)

4. Простота

Требования к программным реализациям алгоритмов

1. Надежность(без ошибок)

2. Работоспособность

3. Переносимость

4. Поддерживаемость

5. Простота

Версия

Аппроксимация состоит в том, что данную функцию f(x) приближенно заменяют (аппроксимируют) некоторой другой функцией, так, чтобы отклонение (x) от f(x) в заданной области [a,b] было минимально возможным, при этом функцию f(x) называют аппроксимируемой, а функцию (x) аппроксимирующей.

При приближении на непрерывном множестве точек отрезка [a,b] аппроксимацию называют непрерывной (или интегральной). Если приближение строится на заданном дискретном множестве точек {x_i} i=0,1,... отрезка [a,b], то аппроксимацию называют точечной.

Если аппроксимирующая функция (x) строится для всего отрезка [a,b] на котором задана функция f(x), то говорят о глобальной аппроксимации, если же весь отрезок [a,b] разбит на частичные отрезки и на каждом используется своя аппроксимирующая функция, то говорят о локальной аппроксимации.

Равномерное и среднеквадратичное приближения. Если приближение строится таким образом, что величина отклонения (модуль разности двух функций f(x) и (x)) удовлетворяет условию

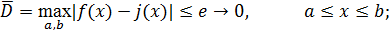(2.2)

то такое приближение (2.2) называют равномерным приближением.

Часто используется среднеквадратичное приближение функции f(x) функцией (x). Здесь стараются получить минимальную величину среднеквадратичного значения модуля разности аппроксимируемой и аппроксимирующей функций на всем отрезке [a,b]:

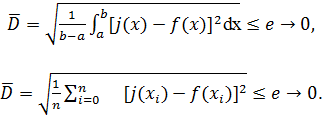(2.3)

Первая формула используется при непрерывной аппроксимации, а вторая при дискретной аппроксимации.

Версия

Метод Гаусса

Этот метод основан на приведении методом исключения системы к треугольному виду (прямой ход):

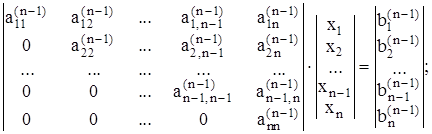(2.4)

а затем решение этой системы начиная с x_n, далее x_n-1 и т.д. до x₁ (обратный ход).

Если система сразу сводится к диагональному виду, то такой метод называется методом Жордана-Гаусса.

Для уменьшения погрешности округления при сведении матрицы А к треугольному виду выбирается максимальный элемент в столбце или в строке и с помощью перестановок он делает главным (схема частичного выбора). Если главный элемент выбирается во всей матрице, то схема носит название глобального выбора.

Алгоритм решения системы из n уравнений методом Гаусса с выбором главного элемента по столбцам выглядит следующим образом.

Прямой ход.На k шаге выбирается главный элемент в k столбце. Пусть это будет элемент в j -ой строке 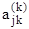, k£j£n. Верхний индекс в скобках указывает, что коэффициенты уравнения получены после (k-1) шага исключения.

Перестановкой j и k строк делает этот элемент диагональным.

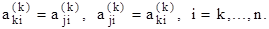
Далее производим исключение x_k из уравнений с номерами k+1,...,n с помощью соотношения:

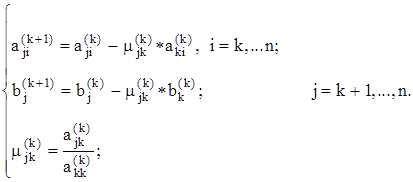(2.5)

После n-1 шагов приходим к системе уравнений (2.4) с треугольной матрицей.

Обратный ход

Из последнего уравнения находим 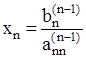. Далее определяем 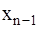, а затем 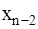и т.д. до x₁ c помощью соотношения:

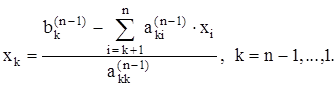(2.6)

Метод прогонки

г) метод прогонки. Данный метод применяется для решения трех диагональных систем:

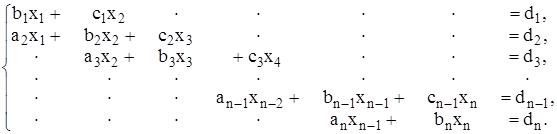
(2.9)

Метод состоит из двух этапов прямой прогонки - и обратной прогонки.

Прямая прогонка: Величина x_i выразим через x_i+1 с помощью коэффициентов A_i, B_i

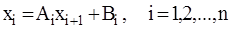. (2.10)

Из первого уравнения находим значения A₁ и B₁:

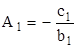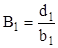, . (2.11)

Подставляя x₁=A₁·x₂+B₁ во второе уравнение (2.9) имеем:

a₂(A₁x₂+B₁)+b₂x₂+c₂x₃=d₂,

или

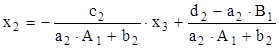
Отсюда согласно (2.10) находим A₂ и B₂

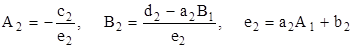, (2.12)

т.е. зная A₁ и B₁ по этой формуле мы можем вычислить A₂ и B₂. Аналогично подставляя значение x_i-1=A_i-1x_i+B_i-1 в i уравнение имеем:

a_i(A_i-1x_i+B_i-1)+b_ix_i+c_ix_i+1=d_i, i=1,2,...n.

Если в формуле (2.12) индекс 1 заменить на индекс i-1, а индекс 2 - на индекс i, то получим общую формулу для прямой прогонки:

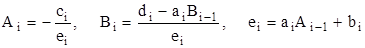, i=2,...,n; (2.13)

которая позволяет определить последующие значения A_i, B_i через предыдущие A_i-1, B_i-1.

После n шагов получим значения A_n и B_n. Так как c_n=0, то A_n=0. Следовательно на основание (2.10) имеем: x_n=B_n.

Обратная прогонка состоит в последовательных вычислениях по формуле (2.10) значений x_n-1, x_n-2 и т.д. до x₁.

Если для трех диагональной системы выполнены условия çb_iç³ça_iç+çc_iç, ½b_i½>½a_i½, i=1,...,n, то эта система имеет единственное решение.

Интерполяция сплайнами

Сплайн (от англ. слова “splane” - гибкий) это функция, которая на всем отрезке интерполяции непрерывна вместе со своими k первыми производными (k£m-1) и на каждом частичном отрезке представляет алгебраический многочлен (полином) степени m.

См. стр 55 (Турчак)

Точность интерполяции

Погрешность интерполяции R_n(x) зависит от числа узлов n и равна:

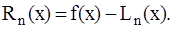(2.11)

В узлах интерполяции погрешность равна нулю. Ее величина зависит от вида аппроксимирующей функции и вычисляется по следующей формуле:

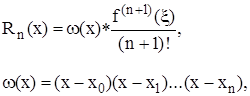(2.12)

где x неизвестная точка на отрезке [x₀,x_n].

Для равномерного распределения узлов, когда x_i-x_i-1=h, для всех i=1,2,...,n (равномерная сетка с шагом h) можем записать:

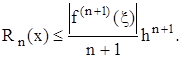
Требования к вычислительным программам

Требования к программным реализациям алгоритмов

1. Надежность(без ошибок)

2. Работоспособность

3. Переносимость

4. Поддерживаемость

5. Простота

Метод ячеек

Пусть требуется вычислить двукратный интеграл в области G(a£x£b, c£y£d):

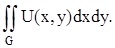
С помощью узлов x_i (i=0,1,..n) и y_j (j=0,1,...,m) и прямых, проходящих через эти узлы: x=x_i и y=y_j, разобьем область G на (n×m) прямоугольных ячеек, имеющих площадь:

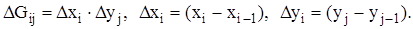
Выбираем в этой ячейке центральную точку:

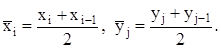
Будем считать, что интеграл для каждой ячейке приближенно равен:

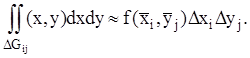(2.12)

Суммируя по всем ячейкам имеем:

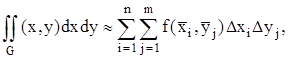(2.13)

при этом погрешность, когда все ячейки имеют одинаковую площадь 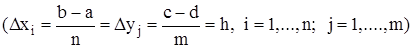будет равна

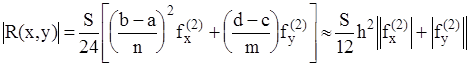; (2.14)

где S - площадь области G, m и n - количество узлов по координатам x,y; 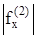, 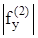- максимальное значение вторых частных производных по соответствующим координатам.

Версия

Метод простой итерации.Уравнение f(x)=0 преобразуют к виду удобному для организации итерации: x=j(x), при этом функция j(x) называется итерационной функцией. На отрезке локализации [a,b] выбирается начальное приближение x=x₀ и вычисляется x₁=j(x₀). Продолжая этот процесс имеем:

.

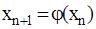Если существует 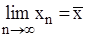, то получаем равенство: 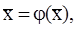где 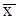- корень. Метод сходится при 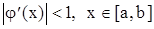, а при 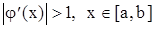- расходится.

Критерий окончания:

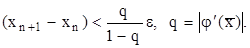
Метод касательных (метод Ньютона).Выбирается точка x₀Î[a,b] и в ней проводится касательная к графику функции y=f(x) и за новое приближение x₁ принимается точка, в которой касательная пересекает ось OX и т.д. В итоге получаем итерационную формулу Ньютона:

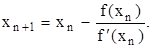(2.6)

Необходимым и достаточным условием сходимости метода Ньютона на отрезке локализации xÎ[a,b] являются:

f¢(x)¹0, - (необходимое условие); (2.7)

f¢¢(x)¹0 - (достаточное условие);

т.е. знакопостоянство первой и второй производной на отрезке локализации.

Версия

Пусть имеется следующая система нелинейных уравнений:

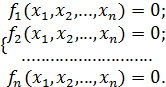(6.5)

Как уже отмечалось выше, для одной переменной метод Ньютона использует замену искомого уравнения уравнением прямой или, как еще говорят, производит линеаризацию исходного уравнения. Пусть имеется k - ое приближение: 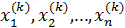. Разложим левые части системы уравнений в ряд Тейлора и учтем только линейные члены:

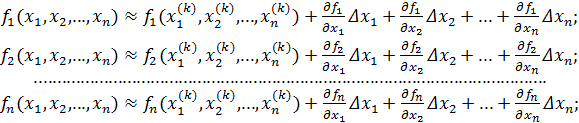(6.6)

где 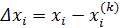, i=1,2,...,n; а частные производные вычисляются в точке k-го приближения: x₁=x₁^(k), x₂=x₂^(k),...,x_n=x_n^(k).

Заменим в исходной системе нелинейные функции f_i(x₁,x₂,...,x_n) на правые части этих приближенных равенств, которые являются линейными функциями относительно переменных x_i, i=1,2,...,n. В итоге получим следующую систему линейных уравнений относительно переменных x_i, i=1,2,...,n:

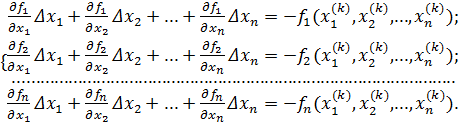(6.7)

Из этой системы можно определить значения x_i, i=1,2,...,n и вычислить значения k+1-приближения: 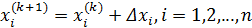. Данная система уравнений представляют собой метод Ньютона для системы нелинейных уравнений.

Определитель этой системы называетсяякобианом.

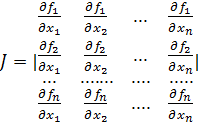. (6.8)

Для существования решения якобиан должен быть отличен от нуля для каждого шага итерации.

Критерий окончания. Итерационный процесс продолжается до тех пор, пока не выполнятся условия: 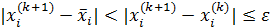, для всех i=1,2,...,n.

Погрешность интерполяции

См. «Точность интерполяции»

Погрешность интерполяции R_n(x) зависит от числа узлов n и равна:

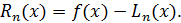(2.11)

В узлах интерполяции погрешность равна нулю. Ее величина зависит от вида аппроксимирующей функции и вычисляется по следующей формуле:

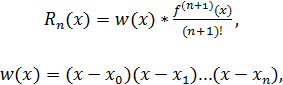(2.12)

где x неизвестная точка на отрезке [x₀,x_n].

Для равномерного распределения узлов, когда x_i-x_i-1=h, для всех i=1,2,...,n (равномерная сетка с шагом h) можем записать:

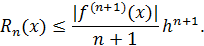
Экзаменационный билет № 28

Математическое моделирование. Основные этапы математического моделирования

Математическое моделирование – предмет исследования объектов и явлений окружающего наш мир с помощью их приближенного описания на языке математики – математических моделей.

Процессы математического моделирования:

1. Построение модели

2. Постановка, исследование, решение математической задачи

3. Проверка модели на графике