Алгоритм поиска точки минимума методом дихотомии
Алгоритм поиска минимума функции сводится к выполнению следующих этапов.
1 этап. Задается начальный интервал неопределенности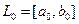 
и 
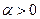- требуемая точность, 
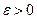- малое положительное число.
2 этап. Задать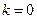 
.
3 этап. Вычислить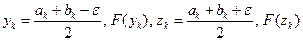 
.
4 этап. Если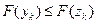 
, принять 
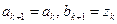и перейти к этапу 5.
Если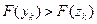 
, принять 
.
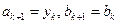5 этап. Вычислить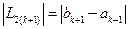 
и проверить условие окончания:
Если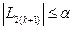 
, то процесс поиска завершается и 
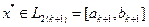. В качестве приближенного решения принимают середину последнего интервала 
.
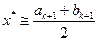Если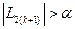 
, то принять 
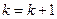и перейти к этапу 3.
Для оценки сходимости метода используется характеристика относительного уменьшения начального интервала неопределенности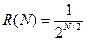 
, где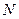 
количество вычислений функции.
Метод золотого сечения
В методе золотого сечения в качестве двух внутренних точек выбираются точки золотого сечения.
Точка производит золотое сечение, если отношение длины всего отрезка к большей части равно отношению большей части к меньшей части. На отрезке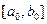 
имеются две симметричные относительно его концов точк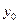и 
и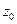 
:
.
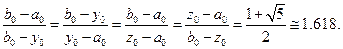Точка 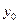производит золотое сечение отрезка 
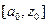, а точка 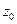- отрезка 
.
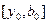Метод относится к последовательным стратегиям. Задается начальный интервал неопределенности и требуемая точность. Алгоритм опирается на анализ значений функции в двух точках. В качестве точек вычисления функции выбираются точки золотого сечения. На каждой итерации, кроме первой, требуется только одно новое вычисление функции. Поиск заканчивается, если длина текущего интервала неопределенности меньше заданной величины.
Алгоритм поиска точки минимума методом золотого сечения
Алгоритм поиска минимума функции сводится к выполнению следующих этапов.
1 этап. Задается начальный интервал неопределенност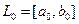и и 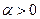- требуемая точность.
2 этап. Задать .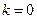
3 этап. Вычислить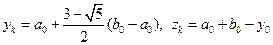 
.
4 этап. Вычислить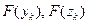 
.
5 этап. Если 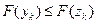, то принять 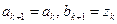и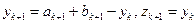 
. Перейти к этапу 6.
Если 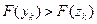, принять 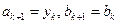и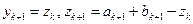 
.
6 этап. Вычислить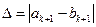 
и проверить условие окончания поиска. Если 
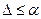, процесс поиска прекращается и 
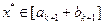. В качестве приближенного решения принимают середину последнего интервала .
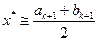Если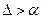 
, принять 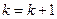и перейти к этапу 4.
Метод Фибоначчи
В методе Фибоначчи реализована последовательная стратегия, обеспечивающая максимальное гарантированное сокращение интервала неопределенности при заданном количестве вычисления функции. Эта стратегия опирается на числа Фибоначчи, определяемые по формуле
.
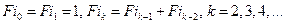Последовательность чисел Фибоначчи имеет вид 1,1,2,3,5,8,13,23,34,55,89,144,233,.. .
Метод относится к последовательным стратегиям. Задается начальный интервал неопределенности и количество вычислений функции. Алгоритм опирается на анализ значений функции в двух точках. Точки вычисления функции находятся с использованием последовательности из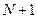 
чисел Фибоначчи. На каждой итерации, кроме первой, требуется только одно новое вычисление функции. Поиск заканчивается, если длина текущего интервала неопределенности меньше заданной величины.