Окончательные результаты для выбора наилучшей модели

Уравнение регрессии	Параметры
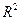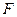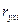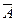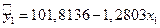	0,0001	0,0048	0,0113	85,5423
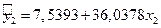	0,5641	49,1744	0,7511	23,4575
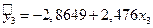	0,7639	122,9488	0,8740	21,8191

Все модели имеют практически одинаковые показатели, кроме модели 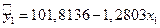, которая является статистически незначимой. Наилучшие показатели среди таких показателей как коэффициент детерминации 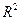, 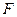-критерий Фишера и средняя ошибка аппроксимации 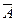, имеет модель .

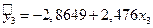Прогнозирование модели

Оценка адекватности модели

Оценим качество построенной модели 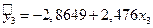, исследуя адекватность.

Таблица 5

№
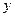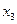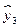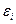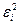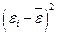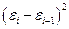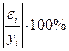			44,1791	-6,1791	38,1813	38,1687	–	16,2608
	62,2		86,2711	-24,0711	579,4179	579,3688	320,1082	38,6995
			98,6511	26,3489	694,2645	694,3183	2542,1892	21,0791
	61,1	34,8	83,2999	-22,1999	492,8356	492,7903	2357,0013	36,3337
		18,7	43,4363	23,5637	555,2480	555,2960	2094,2696	35,1697
		27,7	65,7203	27,2797	744,1820	744,2377	13,8104	29,3330
			143,2191	-25,2191	636,0030	635,9516	2756,0405	21,3721
			106,0791	25,9209	671,8931	671,9459	2615,2606	19,6370
	92,5		135,7911	-43,2911	1874,1193	1874,0310	4790,2587	46,8012
			113,5071	-8,5071	72,3708	72,3534	1209,9107	8,1020
			41,7031	0,2969	0,0881	0,0888	77,4974	0,7069
			106,0791	18,9209	358,0005	358,0391	346,8780	15,1367
			135,7911	34,2089	1170,2488	1170,3186	233,7323	20,1229
			36,7511	1,2489	1,5598	1,5623	1086,4286	3,2866
	130,5		160,5511	-30,0511	903,0686	903,0073	979,6105	23,0277
			81,3191	3,6809	13,5490	13,5565	1137,7930	4,3305
			103,6031	-5,6031	31,3947	31,3833	86,1884	5,7174
		59,2	143,7143	-15,7143	246,9392	246,9072	102,2280	12,2768
			120,9351	-35,9351	1291,3314	1291,2581	408,8902	42,2766
			101,1271	58,8729	3466,0184	3466,1385	8988,5183	36,7956
			46,6551	13,3449	178,0864	178,1136	2072,8497	22,2415
			31,7991	9,2009	84,6566	84,6753	17,1740	22,4412
			113,5071	-23,5071	552,5838	552,5358	1069,7584	26,1190
		49,5	119,6971	-36,6971	1346,6771	1346,6023	173,9744	44,2134
		18,9	43,9315	1,0685	1,1417	1,1439	1426,1818	2,3744
			41,7031	-2,7031	7,3067	7,3012	14,2251	6,9310
	86,9	58,7	142,4763	-55,5763	3088,7251	3088,6117	2795,4659	63,9543
			51,6071	-11,6071	134,7248	134,7011	1933,2085	29,0178
			96,1751	-16,1751	261,6339	261,6009	20,8624	20,2189
			222,4511	4,5489	20,6925	20,7018	429,5379	2,0039
			219,9751	15,0249	225,7476	225,7783	109,7460	6,3936
			34,2751	5,7249	32,7745	32,7862	86,5255	14,3123
		18,5	42,9411	24,0589	578,8307	578,8798	336,1388	35,9088
			133,3151	-10,3151	106,4013	106,3802	1181,5081	8,3863
			88,7471	11,2529	126,6278	126,6507	465,1589	11,2529
			115,9831	-10,9831	120,6285	120,6061	494,4273	10,4601
	70,3	34,8	83,2999	-12,9999	168,9974	168,9709	4,0688	18,4920
			115,9831	-33,9831	1154,8511	1154,7818	440,2806	41,4428
			207,5951	72,4049	5242,4695	5242,6173	11318,6066	25,8589
			145,6951	54,3049	2949,0222	2949,1329	327,6330	27,1525
Сумма	4049,5	1681,8	4049,5408	-0,0408	30223,2929	30223,2929	56863,9459	875,6413
Среднее значение	101,2375	42,045	101,2385	-0,0010	755,5823	755,5823	1421,5986	21,8910

5.1.1 Проверка равенства математического ожидания уровней ряда остатков нулю осуществляется в ходе проверки соответствующей нулевой гипотезы 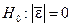. С этой целью строится t-статистика:

,

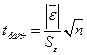где 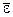– среднее арифметическое значение уровней ряда остатков ;

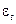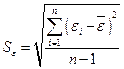– среднеквадратическое отклонение для этой последовательности, рассчитанное по формуле для малой выборки.

Таким образом

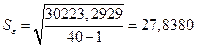
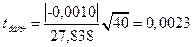
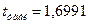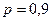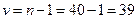при доверительной вероятности и степенях свободы.

Так как 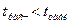, то гипотеза 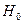принимается.

5.1.2 Проверку случайностей уровней ряда остатковпроведем на основе критерия поворотных точек.

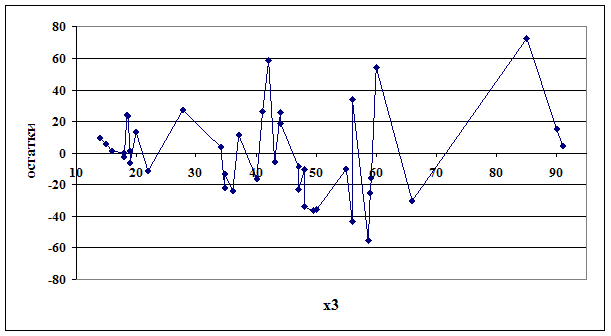
Рисунок 22. График остатков

Критерий случайности отклонений от тренда при уровне вероятности 0,95 можно представить как

.

Таблица 6

Промежуточные данные для применения в оценке адекватности модели

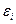№		Точка поворота	№		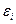Точка поворота
	-6,1791	–		13,3449
	-24,0711			9,2009
	26,3489			-23,5071
	-22,1999			-36,6971
	23,5637			1,0685
	27,2797			-2,7031
	-25,2191			-55,5763
	25,9209			-11,6071
	-43,2911			-16,1751
	-8,5071			4,5489
	0,2969			15,0249
	18,9209			5,7249
	34,2089			24,0589
	1,2489			-10,3151
	-30,0511			11,2529
	3,6809			-10,9831
	-5,6031			-12,9999
	-15,7143			-33,9831
	-35,9351			72,4049
	58,8729			54,3049	–
	Сумма	-0,0408

Фактическое значение точек поворота 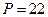. Так как 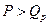, то ряд считается случайным.

Наличие (отсутствие) автокорреляции в отклонениях от модели роста проверяют с помощью критерия Дарбина–Уотсона.

При проверке независимости уровней ряда остатков друг от друга вычисляют значение

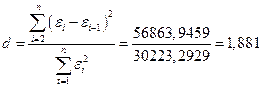
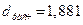не попадает в интервал 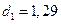и 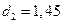. Так как 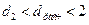, то ряд остатков не коррелирован, т.е. свойство взаимной независимости уровней остаточной компоненты подтверждается.

5.1.4 Соответствие ряда остатков нормальному закону распределенияустановим с помощью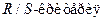

,

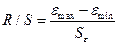где 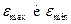соответственно максимальный и минимальный уровни ряда остатков; 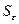– среднеквадратическое отклонение.

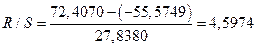
Для 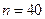задан табулированный интервал 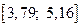. Вычисленное значение 4,5974 попадает между табулированными границами, что означает выполнение нормального закона распределения.

Так как выполнены все четыре условия, построенная модель 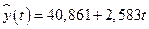является адекватной и ее можно использовать для построения прогнозных оценок.

Расчет прогнозного значения

Если прогнозное значение цены офиса составит: 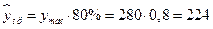тыс. долл., тогда прогнозное значение площади офиса составит:

.

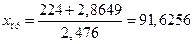Рассчитаем доверительный интервал ,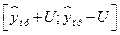

где ,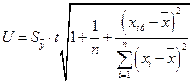

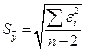
Рассчитаем среднеквадратическое отклонение:

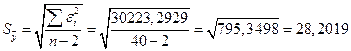
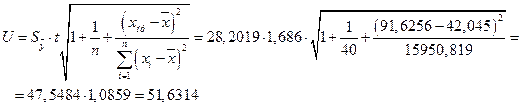
Таким образом, прогнозное значение 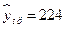будет находиться в интервале 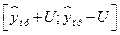, т.е. в интервале .

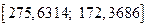Фактические и модельные значения изобразим на графике (см. рис. 22).

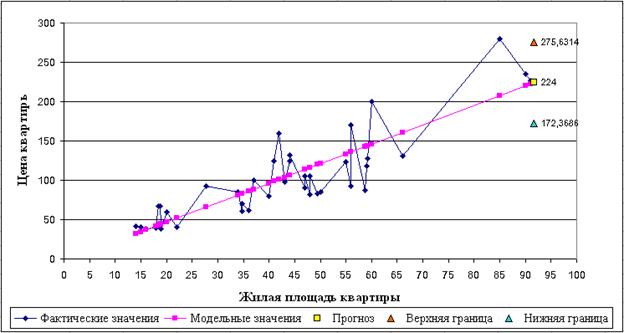
Рисунок 22. График фактических значений, значений модели и точек прогноза

для зависимости цены офиса от его площади