Построим показательную модель.

ŷ = а* b^х

lg у = lg а + х* lg b

обозначим через У = lg у, А = lg а, В = lg b.

У = А + х*В. Значение параметров А и В получим из таблицы.

Таблица 1.3. Расчетные параметры показательной модели регрессии

y	x	У	х2	Ух	У2	ŷ	ε= (yi -ŷ)	ε2	|Аi %|
		2,0828		149,96	4,338	116,561	4,43888	19,70365	3,6685
		1,9243		100,06	3,7029	89,6706	-5,6706	32,15574	6,7507
		2,0755		151,51	4,3079	118,1	0,90027	0,810491	0,75653
		2,0682		153,05	4,2774	119,659	-2,65864	7,068386	2,2723
		2,1106		160,4	4,4546	122,838	6,16152	37,96432	4,77637
		2,1072		166,47	4,4403	127,767	0,23262	0,054113	0,18174
		2,0086		108,46	4,0345	92,0535	9,94647	98,93224	9,75144
		2,0453		139,08	4,1833	110,605	0,39545	0,156382	0,35626
		2,0492		149,59	4,1993	118,1	-6,09973	37,20667	5,4462
		1,9912		127,44	3,965	104,952	-6,95237	48,3355	7,0943
		20,463			41,903	1120,31	0,69387	282,3875	41,0543
112,1	68,5	2,0463	4767,5	140,6	4,1903				4,10543

Рассчитывая параметры модели, получим:

В = 0,00569

А= У – В*х = 2,0463-0,00569*68,5 = 1,6565.

Уравнение запишется в виде: У = А + В*х.

Применив операцию потенцирования, получим:

ŷ = 10^1,6565 * (10^0,00569)^х = 45,342*1,0132^х.

Коэффициент (индекс) корреляции: r = 0,917,

т.е. связь между объемом капиталовложений и выпускаемой продукции можно считать тесной.

Коэффициент детерминации R² = r² = 0,917² = 0,841, т.е. вариация У (объем выпуска продукции) на 84,1% объясняется вариацией фактора Х (объем капиталовложений).

F – критерий Фишера: F = 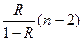= = 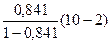42,315. По таблице для a = 0,05; k₁ = m = 1, k₂ = n–m–1 = 8 находим, что F_табл. = 5,32. Т.к. 42,315>5,32, то уравнение регрессии в целом статистически значимо.

Критерий Стьюдента: t_расч = 6,505.

Табличное значение критерия Стьюдента равно: t_табл = (a = 0,05; k = n-2 = 8) = 2,3060.

Сравнивая числовые значения критериев, видно, что t_расч > t_табл, ,т.е. полученное значение коэффициента корреляции значимо.

Средняя относительная ошибка: Е_отн = 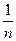∑| |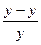* 100% = 4,11%. Таким образом, в среднем расчетные значения ŷ для показательной модели отличаются от фактических значений на 4,11%.

4. Построим гиперболическую модель:ŷ = а + .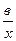

Произведем линеаризацию модели путем замены Х = 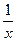, тогда, ŷ = а + вХ.

Параметры а и в найдем с помощью табл. 1.4.

Таблица 1.4. Расчетные параметры гиперболической модели регрессии

T	y	x	Х	уХ	Х2	ŷ	ε= (yi -ŷ)	ε2	|Аi %|
			0,0139	1,68056	0,000193	119,485	1,515	2,295225	1,252
			0,0192	1,61538	0,00037	80,472	3,528	12,44678	4,2
			0,0137	1,63014	0,000188	120,874	-1,874	3,511876	1,575
			0,0135	1,58108	0,000183	122,2263	-5,22629	27,31415	4,467
			0,0132	1,69737	0,000173	124,824	4,176	17,43898	3,237
			0,0127	1,62025	0,00016	128,473	-0,473	0,223729	0,37
			0,0185	1,88889	0,000343	85,674	16,326	266,5383	16,006
			0,0147	1,63235	0,000216	113,518	-2,518	6,340324	2,269
			0,0137	1,53425	0,000188	120,874	-8,874	78,74788	7,923
			0,0156	1,53125	0,000244	106,806	-8,806	77,54564	8,986
Сумма			0,1487	16,4115	0,002257	1123,226		492,4029	50,285
Ср.знач.	112,1	68,5	0,0149	1,64115	0,000226				5,0285

Рассчитаем неизвестные параметры:

в = -7303,258;

а = у – в*Х = 112,1 + 7303,258*0,0149 = 220,919.

ŷ = 220,919 -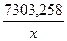

Коэффициент (индекс) корреляции: r = 0,851,

т.е. связь между объемом капиталовложений и выпускаемой продукции можно считать тесной, так как 0,851 > 0,7.

Коэффициент детерминации R² = r² = 0,851² = 0,724, т.е. вариация У (объем выпуска продукции) на 72,4% объясняется вариацией фактора Х (объем капиталовложений).

F – критерий Фишера: F = 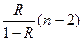= = 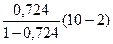20,986. По таблице для a = 0,05; k₁ = m = 1, k₂ = n–m–1 = 8 находим, что F_табл. = 5,32. Т.к. 20,986 > 5,32, то уравнение регрессии в целом статистически значимо.

Критерий Стьюдента: t_расч = 4,582.

Табличное значение критерия Стьюдента равно: t_табл = (a = 0,05; k = n-2 = 8) = 2,3060.

Сравнивая числовые значения критериев, видно, что t_расч > t_табл, ,т.е. полученное значение коэффициента корреляции значимо.

Средняя относительная ошибка: Е_отн = 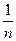∑| |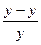* 100% = 5,03%. Т.е. в среднем расчетные значения ŷ для гиперболической модели отличаются от фактических значений на 5,03%.

Рассчитав все параметры по каждой из моделей, сведем их параметры в табл. 1.5.

Таблица 1.5. Основные расчетные параметры моделей регрессии

Модель регрессии	Расчетные параметры
R2	F – критерий Фишера	r	Еотн
Линейная	0,834	40,193	0,913	4,2
Степенная	0,830	39,059	0,911	4,27
Показательная	0,841	42,315	0,917	4,11
Гиперболическая	0,724	20,986	0,851	5,03

Таким образом, наилучшей моделью является показательная модель (по максимуму критерия детерминации и остальным параметрам).

Задание 2.

Задача 2а и 2б.

Для каждого варианта даны по две СФМ, которые заданы в виде матриц коэффициентов модели. Необходимо записать системы одновременных уравнений и проверить обе системы на идентифицируемость.

Таблица 2.1. Исходные данные задачи

Номер варианта

Номер урав- нения

Задача 2а

Задача 2б

переменные

переменные

у1

у2

у3

х1

х2

х3

х4

у1

у2

у3

х1

х2

х3

х4

-1

b13

а11

а12

а13

-1

b12

а11

а12

а13

b21

-1

b23

а23

а24

-1

b23

а21

а23

а24

b32

-1

а31

а33

а34

b32

-1

а31

а33

а34

Система взаимосвязанных уравнений, в которых каждая зависимая переменная у_i представлена как функция остальных зависимых переменных у_к (к ≠ i) и независимых переменных х_i, носит название системы совместных, одновременных уравнений. Ее также называют структурной формой модели (СФМ).

СФМ имеет вид для варианта

2а: у₁ = b₁₃у₃ + а₁₁х₁ + а₁₂х₂ +а₁₂х₃

у₂ = b₂₁у₁ + b₂₃у₃ + а₂₃х₃ + а₂₄х₄

у₃ = b₃₂у₂ + а₃₁х₁ + а₃₃х₃ + а₃₄х₄

2б: у₁ = b₁₂у₂ + а₁₁х₁ + а₁₂х₂ + а₁₃х₃

у₂ = b₂₃у₃ + а₂₁х₁ + а₂₃х₃ + а₂₄х₄

у₃ = b₃₂у₂ + а₃₁х₁ + а₃₃х₃ + а₃₄х₄

СФМ считается идентифицируемой, если выполняется обязательное условие: число эндогенных переменных в i-том уравнении Н и число предопределённых переменных D, которые содержатся в системе, но не входят в данное уравнение, связаны соотношением D+1=H.

Кроме этого, должно выполнятся дополнительное условие:

для матрицы, составленной из эндогенных и экзогенных переменных, отсутствующих в рассматриваемом уравнении, но присутствующих в системе, определитель не равен нулю и ранг матрицы не меньше, чем количество эндогенных переменных в системе без одного.

Проверим каждое уравнение системы 2а:

	у2	х4
	-1	а24
	b32	а34

В 1-м уравнении H = 2, D = 1 – необходимое условие выполнено, матрица имеет вид:

Определитель не равен нулю, а ранг матрицы равен 2, что значит достаточное условие выполнено.

	х1	х2
	а11	а12
	а31

Во втором уравнении H=3, D=2 – необходимое условие выполнено, матрица имеет вид

Определитель не равен нулю, а ранг матрицы равен 2, что значит достаточное условие выполнено.

	у1	х2
	-1	а12

В третьем уравнении H=2, D=1 – необходимое условие выполнено, матрица имеет вид

Определитель не равен нулю, а ранг матрицы равен 2, что значит достаточное условие выполнено.

Таким образом, СФМ 2а идентифицируема.

Проверим каждое уравнение системы 2б:

	у3	х4
	b23	а24
		а34

В первом уравнении H=2, D=1 – необходимое условие выполнено, матрица имеет вид

Определитель не равен нулю, а ранг матрицы равен 2. Это значит, что достаточное условие выполнено.

	y1	х2
	-1	а12

Во втором уравнении H=2, D=1 – необходимое условие выполнено, матрица имеет вид

Определитель равен нулю, значит достаточное условие не выполнено и уравнение не идентифицируемо.

	у1	х2
	-1	а12

В третьем уравнении H=2, D=1 – необходимое условие выполнено, матрица имеет вид

Определитель равен нулю, значит достаточное условие не выполнено и уравнение не идентифицируемо. В целом СФМ 2б не идентифицируема.

Задача 2в

По данным таблицы для своего варианта, используя косвенный метод наименьших квадратов, построить структурную форму модели вида:

у₁ = а₀₁ + b₁₂у₂ + а₁₁х₁ + ε₁,

у₂ = а₀₂ + b₂₁у₁ + а₂₂х₂ + ε₂.

Таблица 2.2. Исходные данные задачи

Вариант	n	у1	у2	х1	х2
		28,3	51,7
	4,4	11,5
	33,1	64,6
	14,6	38,4
	35,9	64,1
	39,5	55,0

Косвенный метод наименьших квадратов (КМНК) применяется при точно идентифицируемой структурной модели. Рассмотрим этот метод на идентифицируемой модели с двумя эндогенными и экзогенными переменными.

у₁ = а₀₁ + b₁₂у₂ + а₁₁х₁ + ε₁,

у₂ = а₀₂ + b₂₁у₁ + а₂₂х₂ + ε₂.

Для построения модели информацию сведем в табл. 2.3.

Таблица 2.3. Фактические данные для построения модели.

n	у1	у2	х1	х2
	28,3	51,7
	4,4	11,5
	33,1	64,6
	14,6	38,4
	35,9	64,1
	39,5
сумма	155,8	285,3
Сред.знач	25,967	47,55	5,83	11,33

Структурную модель преобразуем в приведенную форму модели:

у₁ = d₁₁х₁ + d₁₂х₂ +u₁;

у₂ = d₂₁х₁ + d₂₂х₂ + u₂,

где u₁ и u₂ – случайные ошибки.

Для каждого уравнения приведенной формы при расчете коэффициентов d можно применить МНК.

Для упрощения расчетов можно работать с отклонениями от средних уровней у = у – у_ср и х = х – х_ср (у_ср и х_ср – средние значения). Преобразованные таким образом данные табл. 2.3 сведены в табл. 2.4, здесь же показаны промежуточные расчеты, необходимые для определения коэффициентов d_ik. Переменные, означающие отклонение от средних значений, изображаются далее жирным шрифтом курсивом.

Таблица 2.4. Преобразованные данные для приведенной формы модели

n	у1	у2	х1	х2	у1*х1	х12	х1*х2	у1*х2	у2*х1	у2*х2	х22
	2,333	4,15	1,17	0,667	2,722	1,361	0,778	1,5553	4,8417	2,7667	0,4444
	-21,567	-36,1	-4,83	-10,33	104,2	23,36	49,94	222,86	174,24	372,52	106,78
	7,133	17,05	4,17	2,667	29,72	17,36	11,11	19,021	71,042	45,467	7,1111
	-11,367	-9,15	3,17	-7,333	-36	10,03	-23,2	83,358	-28,98	67,1	53,778
	9,933	16,55	1,17	5,667	11,59	1,361	6,611	56,287	19,308	93,783	32,111
	13,533	7,45	-4,83	8,667	-65,41	23,36	-41,9	117,29	-36,01	64,567	75,111
сумма	-0,002	-0,05			46,87	76,83	3,333	500,37	204,45	646,2	275,33

Для нахождения коэффициентов d_1k первого приведенного уравнения можно использовать следующую систему нормальных уравнений:

∑у₁х₁ = d₁₁∑х₁² + d₁₂∑х₁х₂;

∑у₁х₂ = d₁₁∑х₁х₂ + d₁₂∑х₂².

Подставляя рассчитанные в табл. 2.4 значения сумм, получим:

43,87 = 76,83d₁₁ + 3,333d₁₂

500,37 = 3,333d₁₁ + 275,33d₁₂

Решение этих уравнений дает значения d₁₁ = 0,4924 и d₁₂ = 1,8119.

Первое уравнение приведенной формы модели примет вид:

у_{1 =} 0,4956х₁ + 1,8124х₂ + u₁.

Для нахождения коэффициентов d_2k второго приведенного уравнения можно использовать следующую систему нормальных уравнений:

∑у₂х₁ = d₂₁∑х₁² + d₂₂∑х₁х₂;

∑у₂х₂ = d₂₁∑х₁х₂ + d₂₂∑х₂².

Подставляя рассчитанные в таблице 7 значения сумм, получим:

204,45 = 76,83 d₂₁ + 3,333 d₂₂;

646,2 = 3,333 d₂₁ + 275,33 d₂₂.

Решение этих уравнений дает значения d₂₁ =2,5606 и d₂₂ = 2,3160.

Второе уравнение приведенной формы модели примет вид:

у₂ = 2,5606х₁ + 2,3160х₂ + u₂.

Для перехода от приведенной формы к структурной форме модели найдем х₂ из второго уравнения приведенной формы модели:

х₂ = (у₂ – 2,5606х₁)/2,3160.

Подставим это выражение в первое уравнение приведенной модели, найдем структурное уравнение:

у₁ = 0,4956х₁ + 1,8124(у₂ – 2,5606х₁)/2,3160 = 0,4956х₁ + 0,7826у₂ – 2,0038х₁ =

= 0,7826у₂ - 1,5082х₁.

Таким образом, b₁₂ = 0.7826; а₁₁ = - 1,5082.

Найдем х₁ из первого уравнения приведенной формы модели:

х₁ = (у₁ – 1,8124х₂)/ 0,4956.

Подставим это выражение во второе уравнение приведенной модели, найдем структурное уравнение:

у₂ = 2,3160х₂ + 2,5606(у₁ – 1,8124х₂)/0,4956 = 2,3160х₂ + 5,1667у₁ – 9,3641х₂ =

= 5,1667у₁ - 7,0481х₂.

Таким образом, имеем: b₂₁ = 5,1667; а₂₂ = -7,0481.

Свободные члены структурной формы находим из уравнений:

А₀₁ = у_1,ср –b₁₂у_{2, ср} – а₁₁х_{1, ср} = 25,967 – 0,7826*47,55 + 1,5082*5,83 = -2,45;

А₀₂ = у_{2, ср} – b₂₁у_{1, ср} – а₂₂х_{2, ср} = 47,55 – 5,1667*25,967 + 7,0481*11,31 = -6,90.

Окончательный вид структурной модели:

у₁ = а₀₁ + b₁₂у₂ + а₁₁х₁ + ε₁ = -2,45 + 0,7826у₂ - 1,5082х₁ + ε₁

у₂ = а₀₂ + b₂₁у₁ + а₂₂х₂ + ε₂ = -6,90 + 5,1667у₁ - 7,0481х₂ + ε₂.

ЗАДАНИЕ 3

Принять управленческое решение по оценке стоимости офисов под бизнес.

Исходные данные для моделирования стоимости офиса

№	Цена офиса, Y	Город области, X1	Число комнат в офисе, X2	Площадь офиса, X3
	62,2
	61,1			34,8
				18,7
				27,7
	92,5
	130,5
				59,2
				49,5
				18,9
	86,9			58,7
				18,5
	70,3			34,8

Наименование показателей

Обозначение	Наименование показателя	Единица измерения
Y	цена квартиры	тыс. долл.
X1	город области	1 – Тула
0 – Новомосковск
X2	число комнат в квартире
X3	жилая площадь квартиры	кв. м.

Задание по моделированию и оценке стоимости офиса в Тульской области.

1. Рассчитайте матрицу парных коэффициентов корреляции; оцените статистическую значимость коэффициентов корреляции.
2. Постройте поле корреляции результативного признака и наиболее тесно связанного с ним фактора.
3. Рассчитайте параметры линейной парной регрессии для всех факторов X.
4. Оцените качество каждой модели через коэффициент детерминации, среднюю ошибку аппроксимации и F-критерий Фишера. Выберите лучшую модель.
5. Осуществите прогнозирование для лучшей модели среднего значения показателя Y при уровне значимости 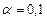, если прогнозное значение фактора Y составит 80% от его максимального значения. Представьте графически: фактические и модельные значения, точки прогноза.
6. Используя пошаговую множественную регрессию (метод исключения или метод включения), постройте модель формирования цены квартиры за счет значимых факторов. Дайте экономическую интерпретацию коэффициентов модели регрессии.
7. Оцените качество построенной модели. Улучшилось ли качество модели по сравнению с однофакторной моделью? Дайте оценку влияния значимых факторов на результат с помощью коэффициентов эластичност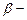и, и 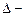коэффициентов.

РЕШЕНИЕ