Пополнение запаса за конечный промежуток времени

Вернемся еще раз к формуле (5) для определения суммарных годовых затрат при мгновенном пополнении запаса: С_год = ic 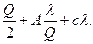Второе и третье слагаемые формулы отражают годовые затраты по заказу партий товаров (сырья) и стоимость закупленных за год товаров. Они постоянны при определении годовых затрат и пополнении запаса за конечные промежутки времени. Первое слагаемое отражает затраты на хранение единицы запаса, умноженные на величину среднего уровня запасов за год (Q/2). При пополнении запаса за конечные промежутки времени средний уровень запаса равен х_max/2 и отражает циклы изменения наличного запаса на складе при пополнении за конечные промежутки времени (рис. 9).

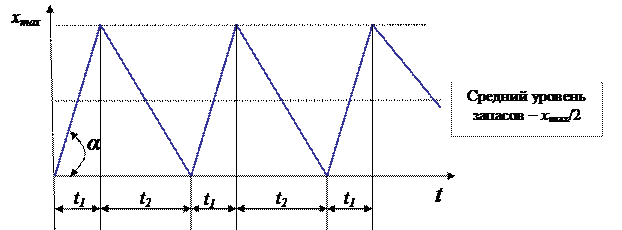
Рис. 9. Изменение запаса на складе при пополнении за промежутки времени

Значение х_maxможно определить по формуле: x_max= tg α t₁. Учитывая, что tg α = λ_П - λ, где λ_П - интенсивность поступления заказа; λ - интенсивность потребления, a t₁ - Q/λ_П, определим x_maxкак x_max= .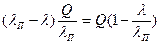

Формула для определения годовых суммарных затрат при пополнении заказа за конечные промежутки времени имеет вид:

C_год=ic 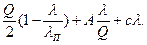(7)

Зная минимум годовых суммарных затрат 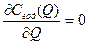, найдем оптимальный размер партии заказа (Q*) пополнения запаса в конечные промежутки времени:

Q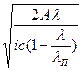^*= (8)

Допущение дефицита

При дефиците запасов возможны две ситуации. 1) требования в отсутствие запасов на складе учитывают и удовлетворяют при поступлении товаров на склад (возможен отрицательный наличный запас на складе, рис. 10).

Рис. 10. Изменение запаса при учете требований в момент дефицита

Вторая ситуация. Требования не учитываются. Циклы изменения наличного запаса на складе для этой ситуации даны на рис. 11. В этом случае определить оптимальный размер партии заказа сложно, так как потери от дефицита зависят от субъективных факторов, например потери клиентов.

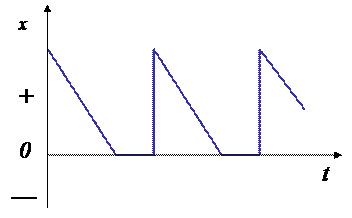
Рис. 11. Изменение запаса без учета требований в момент дефицита

Далее рассмотрим первую ситуацию. На рис. 12 показан 1 цикл изменения запаса на складе при постановке требований на учет. В период времени t' продукция выдается со склада. В период времени t" требования на продукцию регистрируются. Независимо от этих периодов времени период бездефицитной работы может характеризоваться величиной максимального наличного запаса на складе (S).

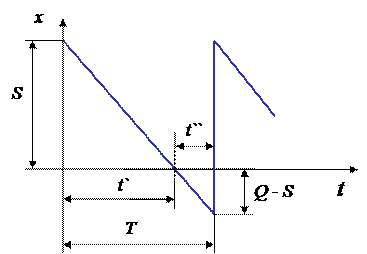
Рис. 12. Цикл изменения запаса на складе при постановке требований на учет

Итак, затраты за цикл Т, по аналогии с предыдущими случаями, могут быть определены по следующей зависимости:

C_Т = А + ic 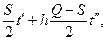(9)

где h — штрафные потери за единицу продукция в единицу времени, обусловленные дефицитом:

С учетом того, что Q = λТ, t' = S/λ, t"=(Q - S)/λ и T = t'+t" имеем:

C_год =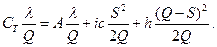

В этом случае неизвестными являются две переменные: размер партии заказа (Q) и максимальный наличный запас на складе (S), поэтому необходимое условие минимума затрат записывается в виде системы:

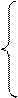
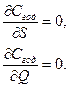
После подстановки выражения для годовых затрат и решения системы получаем следующие выражения для искомых переменных:

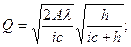(10)

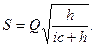(11)

Из формулы (11) ясно, что при очень высоких издержках хранения S®0. Это означает, что поставки осуществляются по зарегистрированным заявкам непосредственно с производства, минуя склад. При низких издержках хранения любой дефицит не выгоден.

Наличие оптовой скидки

В этом случае установить оптимальный размер партии прямым однократным расчетом не удается. Подход к выбору оптимального размера партии можно проиллюстрировать примером.

Задача 6

Дано:Годовое потребление товара λ= 1000000 ед. Затраты на заказ партии А = 28,8 д.е. Структура оптовой скидки и затрат на хранение запасов сведена в таблицу.

Номер варианта	Количество, шт.	Цена за единицу (с), д.е.	Затраты на хранение единицы запасов (ic), д.е.
	0-9999	2,0	0,40
	10 000- 19 999	1,6	0,32
	20 000 и более	1,4	0.28

Используя формулу Уилсона (6), найдем оптимальные размеры партий заказов для каждого из возможных вариантов:

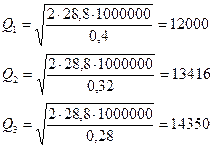
После проведенных расчетов очевидно, что 1-й вариант (закупка партиями менее 10000) не подходит, так как даже при затратах на хранение 0,4 д.е./ед. оптимальный размер партии будет больше 9999.

Сделать выбор между 2-м и 3-м вариантами можно только на основании сравнения суммарных годовых затрат при закупке партиями в 13416 ед. и 20000 ед. Здесь следует отметить, что если бы оптимальный размер партии Q₃ получился больше чем 20000, то однозначно надо было выбирать 3-й вариант.

Формула для вычисления суммарных среднегодовых затрат (5)имеет вид:

C_год=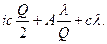

Суммарные среднегодовые затраты при закупке партиями размером 13 416 ед. (2-й вариант) составят:

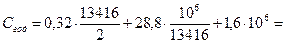1604293 д.е.

Суммарные среднегодовые затраты при закупке партиями размером 20000 единиц (3-й вариант) составят:

C_год= 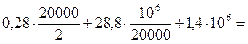1404240 д,е.

На основе приведенных расчетов можно сделать вывод, что целесообразно закупать партиями по 20000 ед. Закупать большими или меньшими партиями будет невыгодно. На рис. 13 показан качественный характер зависимости среднегодовых суммарных затрат от размера партии для данного примера.

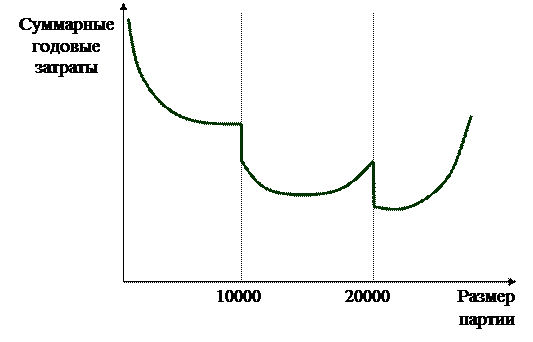
Рис. 13. Зависимость годовых суммарных затрат от размера партии при оптовых скидках