Вычисление центральных углов, образованных направлениями на связующие, трансформационные и геодезические точки
ВВЕДЕНИЕ
Пространственной фототриангуляцией называют метод камерального сгущения съемочного обоснования путем построения и уравнивания фотограмметрической сети. Координаты точек, получаемые в результате уравнивания сети, используются для составления топографических карт, планов, фотопланов и иных документов. Основной целью пространственной триангуляции является максимальное сокращение объема полевых геодезических работ.
Аналитическая фототриангуляция основана на использовании строгих математических зависимостей между координатами точек аэроснимка и местности. Ее построению предшествует измерение координат и параллаксов точек снимков на высокоточных стереокомпараторах, а использование ЭВМ для их обработки открывает возможности как учета всех искажений точек, выражающихся математическими зависимостями, так и применения строгих методов уравнивания результатов измерений методов наименьших квадратов.
Необходимость сгущения планового обоснования в пределах коротких маршрутов может возникнуть также при создании фотопланов с использованием плановой привязки прежних лет, при обновлении или корректуре старых фотопланов и в других случаях.
Работы такого рода не являются массовыми и в настоящее время их выполняют, главным образом, методом графической фототриангуляции, точность которой невелика.
В результате выполнения расчетно-графической работы студентом будут закреплены навыки использования ЭВМ для обработки результатов измерений, получены геодезические координаты главной и четырех трансформационных точек на каждый аэроснимок маршрута.
ВЫЧИСЛЕНИЕ ДЛИНЫ ПЕРВОГО БАЗИСА И ЕГО ДИРЕКЦИОННОГО УГЛА
Длину первого базиса находят из решения обратной геодезической задачи по формуле:
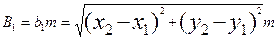, (2)
где X1,2, Y1,2 – отсчёты на главные точки снимков при наблюдении первой стереопары маршрута, т - знаменатель масштаба аэросъемки. Дирекционный угол первого базиса будет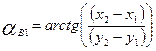 
. Приведенные формулы реализуются программой Simplex (рисунок 1).
Значения B1 и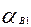 
выписывают, они будут нужны при вычислении геодезических координат главных точек снимков.
Исходные данные для расчетов выполняются сначала для контрольного примера. Порядок ввода данных и их значения для контрольного примера приведены в таблице 3.
Таблица 3 – Порядок ввода исходных данных для контрольного примера
| Вводимая величина | Значение |
| Х1 | -6 |
| Y1 | |
| Х2 | -3 |
| Y2 | |
| m |
При вводе исходных данных необходимо ввести число ограничений – 5, переменных – 1. Для контрольного примера (число ограничений – 5, число переменных – 1.)
После ввода данных необходимо сохранить их и получить решение (рисунок 2).
Решение: В1 = 3,1622776, αВ1 = 108,43495.
ВЫЧИСЛЕНИЕ ПРЕДВАРИТЕЛЬНЫХ КООРДИНАТ ГЛАВНЫХ ТОЧЕК СНИМКОВ
Сеть фототриангуляции предварительно строят в условной фотограмметрической системе первого аэроснимка. В этой системе ось X направлена вдоль первого базиса, а ось Y-ей перпендикулярна. Пространственные координаты главной точки первого аэроснимка принимают условно. Второй базис сети (первое ромбическое звено) находят по формуле (рисунок 4).
В2 =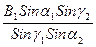 
, (3)
Аналогично вычисляют и все остальные, базисы. Их дирекционные углы будут: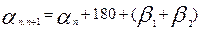 
, (4)
Приращения координат находят, по формулам прямой геодезической задачи с учетом направлений осей фотограмметрической системы:
, 
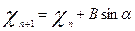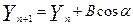, (5)
Приведенные формулы реализуются программой Simplex. Предварительные координаты главных точек можно выписать лишь те, которые будут использованы при построении прямой засечки на опорные точки. Расчеты по приведенной формуле выполняют с помощью программы Simplex. (рисунок 1).
Исходные данные для расчетов выполняются сначала для контрольного примера. Порядок ввода данных и их значения для контрольного примера приведены в таблице 4.
Таблица 4 – Порядок ввода исходных данных для контрольного примера
| Вводимая величина | Значение |
| αВ1 | 108,434 |
| α1 | 63,434 |
| γ1 | 45,00 |
| α2 | 50,906 |
| γ2 | 53,130 |
| В1 | 3,162 |
| β1 | 71,565 |
| β2 | 75,963 |
| Х1усл | -6 |
| Y1усл |
При вводе исходных данных необходимо ввести число ограничений – 10, число переменных – 1.
После ввода данных необходимо сохранить их и получить решение (рисунок 2).
Решение: β1 = 71,56505, β2 = 75,963457, Х2 = -3, Y2 = 0, Х3 = +1, Y3 = +1.
СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ
1. Практические рекомендации к лабораторным работам по фотограмметрии (специальность 1508)/ Гуткин В.Л., Бейчук О.Н., Петрова М.Л. [и др.]; Новочерк. инж.- мелиор. институт., каф. землеустройства. – Новочеркасск, 1988. – 116 с.
2. Назаров А.С. Фотограмметрия / Назаров А.С. Мн.: ТетраСистемс, 2006. – 368 с.
3. Обиралов А. И. и др. Фотограмметрия./ Обиралов А. И., Лимонов А. Н., Гаврилова Л. А. Учебное пособие. – М.: КолосС, 2002.
Учебно-методическое издание
Кривоконева Елена Юрьевна
Мещанинова Елена Германовна
СГУЩЕНИЕ ПЛАНОВОГО СЪЕМОЧНОГО ОБОСНОВАНИЯ МЕТОДОМ АНАЛИТИЧЕСКОЙ РАДИАЛЬНОЙ ФОТОТРИАНГУЛЯЦИИ
Методические указания для выполнения расчетно-графической работы для студентов обучающихся по специальностям 120301 – «Землеустройство»,
120302 – «Земельный кадастр»
Компьютерный набор и графика Кривоконева Е.Ю., Мещанинова Е.Г.
Подписано к печати Формат 60´84 1/16
Объем 1,5 п. л. Тираж экз. Заказ
Типография НГМА 364428, г. Новочеркасск, ул. Пушкинская 111
ВВЕДЕНИЕ
Пространственной фототриангуляцией называют метод камерального сгущения съемочного обоснования путем построения и уравнивания фотограмметрической сети. Координаты точек, получаемые в результате уравнивания сети, используются для составления топографических карт, планов, фотопланов и иных документов. Основной целью пространственной триангуляции является максимальное сокращение объема полевых геодезических работ.
Аналитическая фототриангуляция основана на использовании строгих математических зависимостей между координатами точек аэроснимка и местности. Ее построению предшествует измерение координат и параллаксов точек снимков на высокоточных стереокомпараторах, а использование ЭВМ для их обработки открывает возможности как учета всех искажений точек, выражающихся математическими зависимостями, так и применения строгих методов уравнивания результатов измерений методов наименьших квадратов.
Необходимость сгущения планового обоснования в пределах коротких маршрутов может возникнуть также при создании фотопланов с использованием плановой привязки прежних лет, при обновлении или корректуре старых фотопланов и в других случаях.
Работы такого рода не являются массовыми и в настоящее время их выполняют, главным образом, методом графической фототриангуляции, точность которой невелика.
В результате выполнения расчетно-графической работы студентом будут закреплены навыки использования ЭВМ для обработки результатов измерений, получены геодезические координаты главной и четырех трансформационных точек на каждый аэроснимок маршрута.
ВЫЧИСЛЕНИЕ ЦЕНТРАЛЬНЫХ УГЛОВ, ОБРАЗОВАННЫХ НАПРАВЛЕНИЯМИ НА СВЯЗУЮЩИЕ, ТРАНСФОРМАЦИОННЫЕ И ГЕОДЕЗИЧЕСКИЕ ТОЧКИ
Вычисление центральных углов, образованных направлениями на связующие, трансформационные и геодезические точки осуществляется по формуле
cos θ =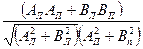 
(1)
где Ал,п=Ул,п-Ув;
Вл,п=-(Хл,п - Хв);
Хл,п; Ул,п – отсчеты по шкалам стереокомпаратора на точки, определяющие левое и правое направления угла;
Хв, Ув- отсчеты на вершину угла.
Расчеты по приведенной формуле выполняют с помощью программы Simplex (рисунок 1).
Исходные данные для расчетов выполняются сначала для контрольного примера. Порядок ввода данных и их значения для контрольного примера приведены в таблице 1.
Таблица 1 – Порядок ввода исходных данных для контрольного примера
| Вводимая величина | Значение |
| ХВ | 84,39 |
| YВ | -3,14 |
| рВ | 82,092 |
| qВ | -4,485 |
| ХЛ | 2,09 |
| YЛ | -2,85 |
| pЛ | 78,140 |
| qЛ | -5,827 |
| ХП | 42,94 |
| YП | 37,54 |
| pП | 79,730 |
| qП | -4,760 |
При вводе исходных данных необходимо ввести число ограничений – 12, переменных – 12. (Для контрольного примера число ограничений – 12, переменных – 1.)
 |
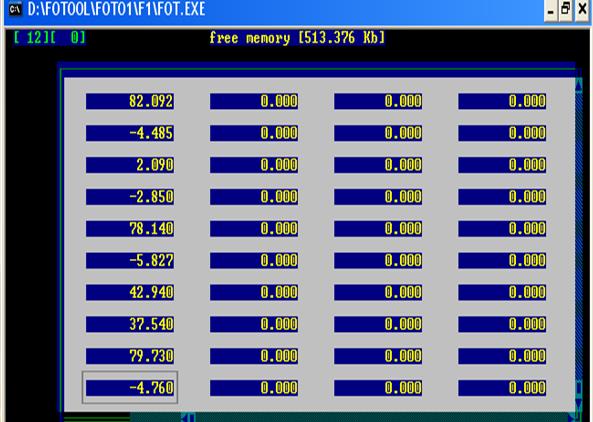Рисунок 1 – Пример ввода исходных данных контрольного примера
После ввода данных необходимо сохранить их и получить решение (рисунок 2).
 |
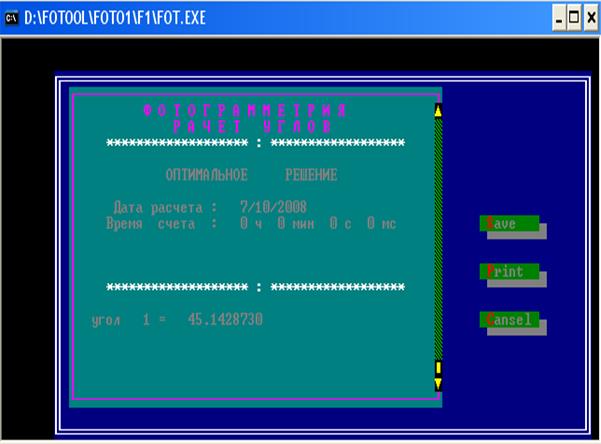Рисунок 2 – Результат решения контрольного примера
Результаты вычисления выписывают в журнал-схему (рисунок 3), которую составляют для каждой стереопары.
 |
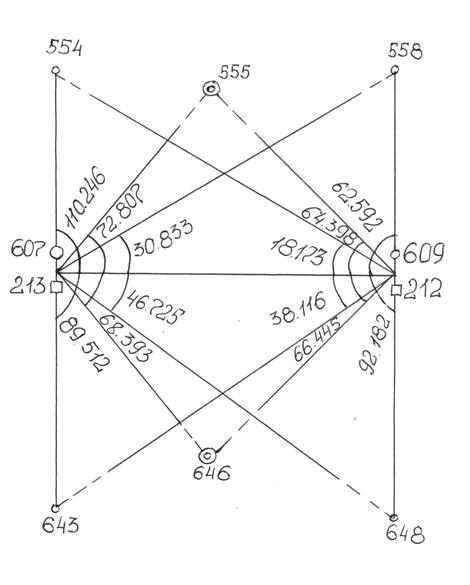Рисунок 3 – Журнал-схема определения центральных углов на стереопаре 213-212