Использование метода ЛАФЧХ для синтеза регуляторов манипулятора с гибким стержнем

Студент Скалов Богдан Юрьевич

курс 4 группа бСАУП-41

Руководитель

доцент, к.т.н., доцент ___________________ А.Б. Смарунь

должность, ученая степень, уч. звание подпись, дата Инициалы Фамилия

Допущен к защите

Протокол № 5 от «2» «ноября» 2016 года

Зав. кафедрой Прикладная математика и системный анализ

профессор, д.ф.-м.н., профессор ___________________ А.И. Землянухин

должность, ученая степень, уч. звание подпись, дата Инициалы Фамилия

Саратов 2017 г

Руководитель

доцент, к.т.н., доцент ___________________ А.Б. Смарунь

должность, ученая степень, уч. звание подпись, дата Инициалы Фамилия

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ

ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ

«САРАТОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

ИМЕНИ ГАГАРИНА Ю.А.»

Институт Физико-технический ________ ________________________

Кафедра Прикладная математика и системный анализ___________________

Направление 27.03.03 – Системный анализ и управление____________________

ЗАДАНИЕ

На выпускную квалификационную работу

Студенту Скалову Богдану Юрьевичу

фамилия, имя, отчество

Тема ВКР: Использование метода ЛАФЧХ для синтеза регуляторов манипулятора с гибким стержнем

утверждена на заседании кафедры, протокол № 5 от «2» ноября 2016 г.

Дата защиты «20» июня 2017 г.

Оценка защиты ______________________

Секретарь ГЭК ______________________ Федорова О.С.

подпись

Саратов 2017 г

Целевая установка и исходные данные

Целью работы является исследование возможности применения метода логарифмических амплитудно-частотных характеристик для синтеза регулятора системы управления манипулятором с упругим стержнем.

Разработать корректирующее устройство для манипулятора, добиваясь максимального качества переходных процессов.

Размерная частота среза скорректированной системы управления не должна превышать допустимой для электро-механических систем ≈ (100 – 150) 1/с.

Коэффициент безразмерного внутреннего демпфирования по Фойгту: 4.8E-3.

Безразмерный коэффициент демпфирования серводвигателя k0=0.015.

Конструктивные параметры манипулятора

Материал стержня – сталь; Длина стержня – 2 м; Внешний радиус – 0.004 м;

Толщина стенки – 0.00049 м;

Материал вала – титан; Длина вала – 0.5 м; Внешний радиус – 0.022 м;

Внутренний радиус – 0.01 м;

Материал груза (форма цилиндр) – сталь; Радиус груза – 0.01 м.

№	перечень чертежей, подлежащих разработке	формат, кол-во
	«Тема выпускной квалификационной работы»	Power Point, 1
	«Актуальность работы»	Power Point, 1
	«Цель работы»	Power Point, 1
	«Схема системы управления манипулятора»	Power Point, 1
	«Механическая схема манипулятора»	Power Point, 1
	«Уравнения движения манипулятора в размерной форме»	Power Point, 2
	«Характерные переменные и параметры»	Power Point, 1
	« Уравнения движения манипулятора в безразмерной форме»	Power Point, 1
	«Структурная схема системы управления»	Power Point, 1
	«Исходная ЛАФЧХ»	Power Point, 1
	«Скорректированная ЛАФЧХ, ФЧХ, ВЧХ, ПП»	Power Point, 1
	«Таблица частотных характеристик»	Power Point, 1
	«Заключение»	Power Point, 1

Руководитель

доцент, к.т.н., доцент ___________________ А.Б. Смарунь

должность, ученая степень, уч. звание подпись, дата Инициалы Фамилия

Содержание расчетно-пояснительной записки

(перечень вопросов, подлежащих разработке)

1. Разработать математическую модель плоского движения манипулятора с вязкоупругим стержнем. Демпфирование в материале стержня учесть по теории Фойгта.

2. От размерной математической модели манипулятора перейти к безразмерной математической модели.

3. Разработать структурную схему системы управления плоским движением манипулятора с вязкоупругим стержнем. Вывести передаточные функции разомкнутой и замкнутой систем управления манипулятором.

4. Применить метод логарифмических частотных характеристик к разработке корректирующего устройства для системы управления плоским движением манипулятора с вязкоупругим стержнем.

5. Исследовать адекватность частотных показателей устойчивости и качества регулирования по логарифмическим амплитудным и фазовым частотным характеристикам применительно к системе управления плоским движением манипулятора с вязкоупругим стержнем.

Основная рекомендуемая литература

1. Андрейченко К.П. Математическое моделирование динамических систем. Учеб. пособие / К.П. Андрейченко, Д.К. Андрейченко. – Саратов: СГТУ, 2000. - 140 с.

2. Андрейченко К.П. Динамическое моделирование манипулятора с гибкой рукой / К.П. Андрейченко, Д.К. Андрейченко // Проблемы машиностроения и надежности машин. - 1996, № 3. – С. 94-100.

3. Андрейченко К.П., Андрейченко Д.К., Смарунь А.Б. Динамическое моделирование линейных дискретно-континуальных систем// Прикладная математика и механика. Т. 64. Вып. 2. 2000. С. 183-195.

4. Бессекерский В.А., Попов Е.Н. Теория систем автоматического управления// В.А. Бессекерский, Е.П. Попов – Изд. 4-е, перераб. и доп. – СПб, Изд-во “Профессия”, 2003. – 752 с.

5. Биргер И. А., Мавлютов Р. Р. Сопротивление материалов: Учебное пособие.— М.: Наука. Гл. ред. физ.-мат. лит., 1986.— 560 с.

6. Седов Л. И., Методы подобия и размерности в механике// Л.И. Седов -М.: Наука, 1977.- 440 с.

Руководитель

доцент, к.т.н., доцент ___________________ А.Б. Смарунь

должность, ученая степень, уч. звание подпись, дата Инициалы Фамилия

Задание принял к исполнению:«01» февраля 2017 г. число, месяц, год

Студент Скалов Б.Ю.___________________

УТВЕРЖДАЮ:

Руководитель ВКР

к.т.н., доцент Смарунь А.Б.___________

«01»февраля 2017 г.

КАЛЕНДАРНЫЙ ГРАФИК

работы над ВКР

№	разделы, темы, их содержание	по плану	фактически	Отметка о выполнении
дата	%	дата	%
	Введение	5.02.2017		5.02.2017		выполнено
	Обзор литературы	15.02.2017		15.02.2017		выполнено
	Постановка задачи	1.03.2017		1.03.2017		выполнено
	Вывод уравнений движения манипулятора	10.04.2017		10.04.2017		выполнено
	Формирование частотных характеристик замкнутой и разомкнутой системы управления манипулятором	20.04.2017		20.04.2017		выполнено
	Построение ЛФЧХА, АЧХ, ВЧХ, переходных процессов системы управления манипулятором.	20.05.2017		20.05.2017		выполнено
	Анализ результатов численного эксперимента, построение графиков	25.05.2017		25.05.2017		выполнено
	Общие выводы по работе. Заключение	1.05.2017		1.05.2017		выполнено
	Оформление ВКР	14.06.2017		14.06.2017		выполнено

Студент ____________________ Б.Ю. Скалов

подпись, дата инициалы, фамилия

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ

ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ

«САРАТОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

ИМЕНИ ГАГАРИНА Ю.А.»

ОТЗЫВ

руководителя о выпускной квалификационной работе

“Использование метода ЛАФЧХ для синтеза регуляторов манипулятора с гибким стержнем”

студента 4 курса Физико-технического института

наименование института

Скалова Богдана Юрьевича фамилия, имя, отчество

прошедшего обучение по направлению

27.03.03 - Системный анализ и управление

код и наименование направления

Работа соответствует заданию, а содержание ВКР основной цели – проверке знаний и степени подготовленности студента по своей специальности.

Работа Скалова Б.Ю. посвящена решению задачи исследования соответствия переходных процессов в системе управления манипулятора с исполнительным устройством в виде вязкоупругого стержня стандартным частотным характеристикам.

Поставленные в работе вопросы раскрыты достаточно полно с обоснованием соответствующих результатов исследования и выводов. Материал квалификационной работы изложен последовательно, логично, математически грамотно, стиль изложения соответствует квалификации бакалавра.

При изучении необходимой литературы и выполнении численного эксперимента с привлечением математических приложений ЭВМ Скалов Б.Ю. проявил достаточную самостоятельность и понимание изучаемого материала. В работе были использованы полученные им при обучении знания в области математики, физики и информатики.

Объем заимствований в выпускной квалификационной работе Скалова Б.Ю. не превышает 40%.

Считаю, что представленная работа удовлетворяет требованиям, предъявляемым к выпускным квалификационным работам, и достойна оценки «хорошо», а ее автор Скалов Богдан Юрьевич заслуживает присвоения ему квалификации «бакалавр» по направлению подготовки 27.03.03 «Системный анализ и управление».

Руководитель ВКР___________________ к.т.н., доцент Смарунь А.Б.

АННОТАЦИЯ

Пояснительная записка к выпускной квалификационной работе содержит 72 листа формата А4, 52 рисунка. Использовано 17 литературных источников.

Ключевые слова:

МАНИПУЛЯТОР, ГИБКИЙ СТЕРЖЕНЬ, МАТЕМАТИЧЕСКАЯ МОДЕЛЬ, ЛОГАРИФМИЧЕСКАЯ АМПЛИТУДНО-ЧАСТОТНАЯ ХАРАКТЕРИСТИКА, ФАЗОВАЯ ЧАСТОТНАЯ ХАРАКТЕРИСТИКА, ЧАСТОТНЫЕ ПОКАЗАТЕЛИ КАЧЕСТВА.

В данной работе разработана математическая модель манипулятора как совокупности дискретных элементов с сосредоточенными по пространству параметрами (абсолютно жесткий вал, датчики первичной информации, усилители, двигатели) и элемента с распределенными по пространству параметрами (вязкоупругий стержень) динамически связанные через границы раздела и в этом смысле являющиеся дискретно-континуальными (распределенными). С использованием широко применяемого инженерами метода логарифмических амплитудных и фазовых частотных характеристик сформировано корректирующее устройство для регулятора системы управления плоским движением манипулятора. Исследована применимость частотных показателей устойчивости и качества регулирования по логарифмическим амплитудным и фазовым частотным характеристикам к системе управления плоским движением манипулятора с вязкоупругим стержнем.

ABSTRACT

Explanatory note to the final qualifying work contains 72 A4 pages, 52 figures. Used 17 of the literary source.

Keywords:

A MANIPULATOR, A FLEXIBLE ROD, THE MATHEMATICAL MODEL, THE LOGARITHMIC AMPLITUDE-FREQUENCY CHARACTERISTICS, PHASE FREQUENCY CHARACTERISTICS, FREQUENCY OF PERFORMANCE.

In this work the mathematical model of the manipulator as a set of discrete elements with lumped according to the space parameters (a perfectly rigid shaft, the primary information gauges, amplifiers, engines) and an element distributed in space parameters (viscoelastic rod) dynamically linked across boundaries and in this sense is a discrete-continuous (distributed). Using widely used by engineers method of logarithmic amplitude and phase frequency characteristics of the generated corrective device for the controller of the control system of the plane motion of the manipulator. Investigated applicability the frequency stability and the quality of regulation on a logarithmic amplitude and phase frequency characteristics to a control system of the plane motion of manipulator with viscoelastic core.

РЕФЕРАТ

Работа состоит из 4 глав, введения, заключения и списка использованной литературы. Работа снабжена 40 рисунками. Имеется 1 таблица.

Во введении обосновывается актуальность темы и рассматриваются методы исследования.

В первой главеприведена постановка задачи исследования, задаются параметры манипулятора и вязкоупругого стержня.

Вторая глава посвящена выводу размерных и безразмерных уравнений движения манипулятора. Получены передаточные функции разомкнутой и замкнутой системы управления манипулятора с вязкоупругим стержнем.

В третьей главе представлены результаты формирования различных корректирующих устройств системы управления манипулятора по методу логарифмических амплитудных и фазовых частотных характеристик. Корректирующие устройства выбиралось таким образом, чтобы получить различные значения основных частотных характеристик, по которым можно судить о качестве регулирования.

В четвертой главе анализируются частотные характеристики, полученные в третьей главе. Показаны пределы их применимости для оценки качества регулирования.

В заключении сформулированы основные выводы по результатам исследования.

В списке использованной литературы указано 17 наименований литературных источников, использованных при написании ВКР.

Текстовая часть ВКР выполнена в текстовом редакторе Microsoft Office Word 2010.

СОДЕРЖАНИЕ

ВВЕДЕНИЕ …………………………………………………………….……........12

1 ПОСТАНОВКА ЗАДАЧИ ИССЛЕДОВАНИЯ…………….…….…………15

1.1. Исходные данные для проектирования манипулятора ……..….…10

1.2 Конструктивные параметры манипулятора ………….…….……....18

2 ВЫВОД УРАВНЕНИЙ ДВИЖЕНИЯ МАНИПУЛЯТОРА С УПРУГИМ СТЕРЖНЕМ И ЗАКРЕПЛЕННЫМ НА ЕГО КОНЦЕ ТВЕРДЫМ ТЕЛОМ …………………………………………………………………………………………….20

2.1 Система автоматического управления манипулятором …………..…...….21

2.2 Механическая схема манипулятора и основные обозначения и упрощения……………………………………………………………………..……..….23

2.3 Размерная математическая модель системы управления манипулятором……………………………………………………………………….…26

2.4 Безразмерная математическая модель системы управления манипулятором ………………………………………………………………………………….………...31

2.5 Решение уравнения движения гибкого стержня………………..………..…38

2.6 Передаточная функция замкнутой системы регулирования манипулятора ……………………………….………………….……………………………………..…38

2.7 Вывод передаточной функции разомкнутой системы регулирования манипулятора …………………..…………………………………………………….…38

3 СИНТЕЗ регулятора для системы управления манипулятором по методу ЛАФЧХ …………………………….…………….…………………………………..…..43

4 ИССЛЕДОВАНИЕ соответствия переходных процессов в манипуляторе иизвестных частотных показателейкачества…………………………….……………50

Заключение………………………………………………………………………...78

СПИСОК ИСПОЛЬЗУЕМЫХ ИСТОЧНИКОВ………………………………...80

ВВЕДЕНИЕ

Важнейшей проблемой создания современных технических систем и выбора режимов их эксплуатации является проблема построения и анализа динамических моделей этих систем.

Многие технические системы состоят из дискретных элементов с сосредоточенными по пространству параметрами (абсолютно жесткие тела, датчики первичной информации, двигатели, усилители) и элементы с распределенными по пространству параметрами (оболочки, упругие стержни, потоки жидкости и газа) динамически связанные через границы раздела и в этом смысле являются распределенными или дискретно-континуальными (ДКС). Системы дифференциальных уравнений движения ДКС, содержащие обыкновенные дифференциальные уравнения и связанные с ними через граничные условия уравнения с частными производными, начальные условия и условия связи , для краткости называют комбинированными динамическими системами (КДС) [1].

На рисунке ниже приведена структурная схема комбинированной динамической системы (КДС).

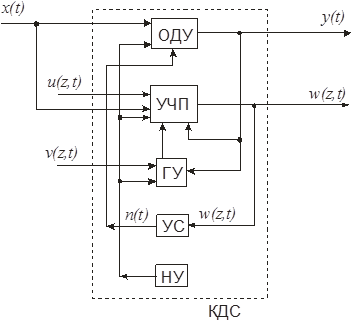
Рис. 1.1

На структурной схеме ОДУ - система обыкновенных дифференциальных уравнений. УЧП - система уравнений с частными производными, граничными условиями (ГУ) при заданных условиях связи (УС) и начальных условиях (НУ). x(t) - сосредоточенное, а u(z,t) и v(z,t) –распределенные возмущения; y(t) – сосредоточеннаяи w(z,t) - распределенная реакции комбинированной динамической системы; z – вектор пространственных координат.

При управлении движением облегченных быстродействующих манипуляционных роботов, ракет, больших космических конструкций, необходимо изначально учитывать деформации их конструктивных элементов. Сложности, связанные с управлением ориентацией космических аппаратов (КА), не имеющих абсолютно жесткой конструкции, впервые проявились в начале 60-х годов, когда, после выведения на орбиту сравнительно небольшого американского спутника "Эксплоурер-Г, он очень быстро потерял устойчивость вследствие непредвиденного эффекта рассеяния энергии закрутки из-за, наличия упругости четырех штыревых антенн. С тех пор и до настоящего времени к этой сложной проблеме привлечено пристальное внимание многих ведущих специалистов (математиков, механиков, инженеров) почти всех стран мира [2].

Как правило в математических моделях деформируемых управляемых объектов уравнения с частными производными движения упругих элементов конструкций заменяются конечномерными аппроксимациями, построенными на матричных конечно-элементных моделях, либо на усеченных разложениях по собственным формам [3]. Разработанное на основе такой приближенной модели деформируемого объекта управляющее устройство может вызвать возбуждение неучтенных форм колебаний и дестабилизировать систему автоматического управления. Этот эффект наблюдаемый, например, в больших космических конструкциях, авторы работы [3] назвали излишним управлением. В работах [4], [5], [6] предложен оригинальный подход к формированию математических моделей комбинированных систем позволяющий учесть весь бесконечный спектр частот и форм колебаний континуальных элементов.

КДС моделируют динамические процессы в облегченных быстродействующих манипуляционных роботах, в больших космических конструкциях, в упругих ракетах, в поплавковых гироскопических приборах и акселерометрах и многих других технических системах.

Задачам управления твердыми телами с вязкоупругими стержнями посвящено большое количество работ [8] – [14]. В этих работах используются такие методы синтеза регуляторов для систем управления как методы параметрического синтеза использующие минимизацию некоторых функционалов. В [12] показано, что система уравнений, моделирующая движение космического аппарата в режиме стабилизации, распадается на три сравнительно независимых канала управления, каждый из которых может исследоваться самостоятельно. В работе [10] также рассматривается один из каналов стабилизации космического аппарата. В [8, 9, 10] математическая модель космического аппарата с упругими стержнями представлена в виде частотных характеристик и, поэтому, для синтеза регулятора можно использовать хорошо разработанные частотные методы и в частности метод логарифмических частотных характеристик [15]. Этот метод достаточно прост, знаком и используется многими инженерами в реальных проектах, позволяет наглядно судить об устойчивости и качестве регулирования систем автоматического управления. В сложных случаях взаимозависимых каналов управления метод позволяет определять начальные значения параметров регуляторов для запуска различных методов оптимизации процессов регулирования. В настоящей работе показана простота и эффективность использования метода логарифмических частотных характеристик для разработки регуляторов манипулятора с упругим стержнем.

Суть метода логарифмических частотных характеристик заключается в следующем [15]. Логарифмические частотные характеристики ( л. ч. х.) включают в себя построенные отдельно на одной плоскости логарифмическую амплитудную характеристику (л. а. х.) и логарифмическую фазовую характеристику (л. ф. х.). Для построения л. а. х. находится L(ω)=20lg|W(jω)|=20lg(A(ω)), где W(jω) – частотная характеристика разомкнутой системы управления. Эта величина выражается в децибелах. Бел представляет собой логарифмическую единицу, соответствующую десятикратному увеличению мощности. Один Бел соответствует увеличению мощности в 10 раз, 2 Бела — в 100 раз, 3 Бела — в 1000 раз и т. д.

Децибел равен одной десятой части Бела. Если бы А(ω) было отношением мощностей, то перед логарифмом в правой части должен был бы стоять множитель 10. Так как А(ω) представляет собой отношение не мощностей, а выходной и входной величин (перемещений, скоростей, напряжений, токов, углов и т. п.), то увеличение этого отношения в десять раз будет соответствовать увеличению отношения мощностей в сто раз, что соответствует двум Белам или двадцати децибелам. Поэтому в правой части стоит множитель 20.

Необходимость логарифмировать модуль частотной передаточной функции приводит к тому, что, строго говоря, л. а. х. может быть построена только для тех звеньев, у которых передаточная функция представляет собой безразмерную величину. Это возможно при одинаковых размерностях входной и выходной величин звена. В дальнейшем изложении будет подразумеваться именно этот случай.

Однако л. а. х, может условно строиться и для тех звеньев, у которых передаточная функция имеет какую-либо размерность. В этом случае некоторая исходная величина, соответствующая размерности передаточной функции, принимается за единицу (например, 1 с^-1, 1 рад и т. п.) и под значением А(ω) понимается отношение модуля частотной передаточной функции к этой исходной единице.

Это же замечание относится и к угловой частоте ω, которая имеет размерность [с^-1] и которую приходится логарифмировать в соответствии с изложенным выше.

Для построения логарифмических аплитудных характеристик и логарифмических фазовых характеристик. используется специальная сетка (рис. 1.2).

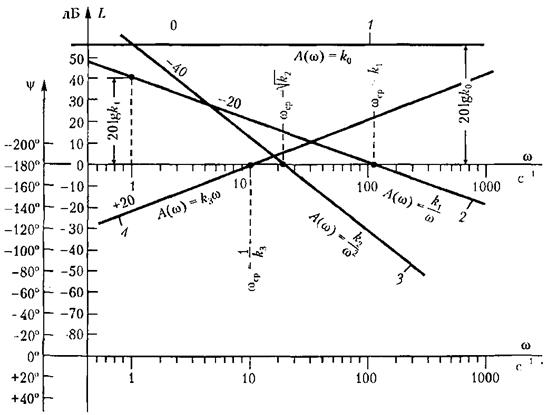
Рис. 1.2

По оси абсцисс откладывается угловая частота в логарифмическом масштабе, т. е. наносятся отметки, соответствующие lgω, а около отметок пишется само значение частоты ω в рад/с.

По оси ординат откладывается модуль в децибелах (дБ). Для этой цели на ней наносится равномерный масштаб. Ось абсцисс должна проходить через точку 0 дБ, что соответствует значению модуля А(ω) = 1, так как логарифм единицы равен нулю.

Ось ординат может пересекать ось абсцисс (ось частот) в произвольном месте. Следует учесть, что точка ω = 0 лежит на оси частот слева в бесконечности, так как lg 0 =-∞. Поэтому ось ординат проводят так, чтобы справа от нее можно было показать весь ход л. а. х. Для построения л. ф. х. используется та же ось абсцисс (ось частот). По оси ординат откладывается фаза в градусах в линейном масштабе (рис. 1.3).

Рис. 1.3

Первой операцией процесса синтеза является построение желаемой ЛАХ. Это построение выполняется на основе требований, которые предъявляются к проектируемой системе управления.

К системам управления обычно в идеале предъявляются следующие требования [15]:

· устойчивость;

· нулевая ошибка в установившемся режиме;

· быстрый и плавный (в идеале – монотонный) переходный процесс;

· подавление шумов;

· робастность (нечувствительность к изменению параметров исходной модели системы).

Устойчивость и робастность обеспечивается определенным видом среднечастотного участка ЛАХ. Этот участок расположен слева и справа от частоты среза ω_ср разомкнутой системы управления. На этом участке ЛАХ на частоте среза ω_ср пересекает ось частот, ф.ч.х. на частоте среза желательно иметь от -150^◦ до -140^◦, наклон среднечастотного участка ЛАХ должен быть

-20 дб на декаду и на концах требуется обеспечить запасы по амплитуде не менее 12 дб. Низкочастотный и высокочастотный участки ЛАХ должны, по возможности, совпадать с ЛАХ исходной системы, управление которой осуществляется, что приводит к упрощению регулятора системы автоматического управления.

Нулевая ошибка в установившемся режиме обеспечивается введением в регулятор интегрирующего звена.

Скорость переходного процесса обеспечивается выбором частоты среза ω_ср разомкнутой системы управления. Чем больше частота среза, тем время переходного процесса меньше. Плавность переходного процесса зависит от вида среднечастотного участка ЛАХ.

Подавление шумов зависит от частоты среза разомкнутой системы управления. Чем меньше частота среза, тем сильнее происходит подавление шумов. Этот пункт противоречит пункту о скорости переходного процесса. В реальности проектировщик принимает компромиссное решение.

Вторым пунктом синтеза является построение ЛАХ исходной системы.

ЛАХ корректирующего устройства регулятора получается в результате вычитания из ЛАХ желаемой ЛАХ исходной системы.

Завершением процесса синтеза является построение переходного процесса.