Исключение выбросов из нестационарных временных рядов
Одним из способов обнаружения «выбросов» во временных рядах, имеющих как случайную, так и систематическую составляющую, является предварительное исключение последней. Второй способ сводится к одновременному решению двух задач: установлению тренда и обнаружению выбросов как исключительно значительных «остатков» (различий между фактическими и ожидаемыми значениями функции отклика, см. главу 4).
После исключения систематических составляющих временной ряд становится стационарным временным рядом, обнаружение выбросов в котором рассмотрено выше (см. § 2.2). Способы исключения тренда являются наиболее простыми по сравнению со способами исключения периодических составляющих, и они рассмотрены в настоящем пособии. Ввиду сложности задачи исключение периодических систематических составляющих, как правило, не проводится. Уменьшение влияния «выбросов» в этом случае осуществляется за счёт операции «сглаживания», см. гл. 3.
Использование инструмента «Регрессия» для обнаружения «выбросов».Инструмент «Регрессия» позволяет не только устанавливать координаты линии тренда, но и одновременно обнаруживать выбросы (см. главу 2). Под «выбросами» здесь следует понимать отклонения от теоретической модели, настолько большие, что они не могут объясняться случайной составляющей временного ряда. Такие отклонения могут свидетельствовать о каком-то сбое, ошибке в получении результата.
Именно отклонение от теоретической модели выражает «Остаток», представляющий собой разницу между фактическим и теоретическим значениями Y. «Стандартизированный остаток» - есть отношение «остатка» к «стандартной ошибке единичного наблюдения регрессионной статистики», определяемой по формуле:
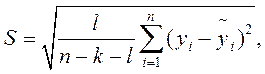 (4.1)
(4.1)
где k - количество исследуемых факторов.
«График остатков» располагается в координатах x - величина остатка, по нему наглядно видны значения «остатка» для разных аргументов, что позволяет обнаружить «выбросы». (Процедура устранения таких «выбросов» называется «цензурированием».) Для этого можно воспользоваться критерием Райта (см. § 2.2). Только вместо используемого в выборке или стационарном временном ряду сравнения со стандартным отклонением здесь значение остатка сравнивается с утроенной «стандартной ошибкой единичного наблюдения регрессионной статистики». В случае если значение остатка превышает эту величину, соответствующее наблюдение следует считать «выбросом» и удалять из временного ряда.
8.4.5 Гармонический анализ в применении к процессам металлообработки. Быстрое преобразование Фурье (БПФ). Кросс-спектральный анализ. Анализ распределённых лагов
Основные понятия и принципы гармонического анализа.
В качестве примера рассмотрим упрощённую схему производства плоскопараллельных мер длины, к которым, как известно, предъявляют особые требования по точности размера. Допустим, что она включает следующие операции:
- фрезерование прокатанной заготовки (цилиндрической фрезой),
- шлифование (черновое, а затем чистовое цилиндрической поверхностью шлифовального круга),
- резка на габаритные размеры
- последовательный по ходу обработки контроль «главного» размера, в результате которого формируется временной ряд и обнаруживается, что периодически размеры выходят за пределы установленного допуска.
Причинами гармонических составляющих «разномера» могут быть:
- эксцентриситет установки и в результате «биение» шлиф. круга,
- неустойчивость, упругие колебания системы СПИД,
- погрешности размера фрезерованной заготовки, вызванные эксцентриситетом установки фрезы, «сглаженные», но не полностью устраненные при последующей обработке
- погрешности размера прокатанной заготовки, вызванные эксцентриситетом установки «рабочих» и «опорных» валков прокатного стана, также «сглаженные», но не полностью устраненные при последующей обработке.
Этих причин возникновения гармонических составляющих колебания размера можно насчитать ещё больше. Каждая из них даёт свой период колебания размера, определяемый длиной окружности инструмента (шлиф. круга, фрезы, прокатного валка) или периодом упругих колебаний системы СПИД. Полностью устранить все причины возникновения этих гармонических составляющих колебания размера не представляется возможным и, как правило, нет такой необходимости. Задача состоит лишь в том, чтобы найти и устранить, по крайней мере, уменьшить главную причину "разномера" и таким образом обеспечить «попадание» размера в поле допуска. Но для поиска надо первоначально найти период (или частоту) этой «главной составляющей», что является непростой задачей, так как мы можем наблюдать лишь результат сложения всех составляющих.
Гармонический анализ, (спектральный анализ) - математическая процедура разложения функции на гармонические составляющие, обратная явлению их сложения, наблюдающемуся в практике, в частности в металлообработке.
Термин "спектральный" - своеобразная метафора для описания природы этого анализа, сходного с физическим явлением разложения белого света на спектральные цветные составляющие различной длины волны (но в нашем случае не с помощью призмы, а с помощью специального математического аппарата.) Таким образом, цель спектрального анализа - разложение комплексных временных рядов с циклическими компонентами, которые, на первый взгляд, выглядят как случайный шум, на несколько основных синусоидальных функций с определенными длинами волн. Зная длины волны, определяют источник колебания, а устраняя этот источник, уменьшают общую дисперсию временного ряда характеристики качества (размера, свойств и т.д.)
Частота и период.Как известно, периодическаяфункция, в частности функции синуса или косинуса, как правило, выражается числом циклов (периодов) в единицу времени - «частотой», которая обычно обозначается греческой буквой ню ( 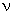 ) или латинской f. «Период»илидлина волны Т функций синуса или косинуса определяется как продолжительность полного цикла. Таким образом, период это обратная величина к частоте: T = 1/
) или латинской f. «Период»илидлина волны Т функций синуса или косинуса определяется как продолжительность полного цикла. Таким образом, период это обратная величина к частоте: T = 1/ 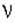 .
.
Общая структура модели
Как было отмечено ранее, цель спектрального анализа - разложить ряд на функции синусов и косинусов различных частот, для определения тех, появление которых особенно существенно и значимо. Один из возможных способов сделать это - решить задачу линейной множественной регрессии, где зависимая переменная - наблюдаемый временной ряд, а независимые переменные или регрессоры: функции синусов всех возможных (дискретных) частот. Такая модель линейной множественной регрессии может быть записана как:
xt = a0 + ∑ [ak*cos(λ k*t) + bk*sin(λk*t)] (8.2)
где λ (лямбда) - круговая частота, выраженная в радианах в единицу времени, т.е. λ = 2*π*νk, π ≈ 3.1416, νk = k/q, k изменяется от 1 до q. Здесь важно осознать, что вычислительная задача подгонки функций синусов и косинусов к данным может быть решена с помощью множественной линейной регрессии. Коэффициенты ak при косинусах и коэффициенты bk при синусах - это коэффициенты регрессии, показывающие степень, с которой соответствующие функции коррелируют с данными. Всего существует q различных синусов и косинусов.
Важно отметить, что сами синусы и косинусы на различных частотах не коррелированы (не связаны) иначе ортогональны. Т.о., здесь рассматривается частный случай разложения по ортогональным полиномам.
Не вдаваясь в подробности, отметим, если n - количество данных, то будет получено n/2+1 функций косинусов и n/2-1 функций синусов. Другими словами, различных синусоидальных волн будет столько же, сколько данных, и можно полностью воспроизвести ряд по основным функциям. В итоге, спектральный анализ определяет корреляцию функций синусов и косинусов различной частоты с наблюдаемыми данными. Если найденная корреляция (коэффициент при определенном синусе или косинусе) велика, то можно заключить, что существует строгая периодичность в данных на соответствующей частоте.
Часто данная структурная модель представлена в комплексных числах; т.е. параметры оцениваемого процесса описаны с помощью действительной и мнимой части преобразования Фурье. Можно также представить комплексные числа как углы; например, можно соединить точку, соответствующую комплексному числу, на плоскости с началом координат и измерить угол наклона этого вектора к горизонтальной оси. В таком виде математические вычисления часто более изящны и проще в выполнении.
Периодограмма
Функции синусов и косинусов независимы (или ортогональны); поэтому можно просуммировать квадраты коэффициентов для каждой частоты, чтобы вычислить периодограмму. Более часто, значения периодограммы вычисляются как:
Pk = (синус-коэффициентk2 + косинус-коэффициентk2) * N/2
где Pk - значения периодограммы на частоте νk , N - общая длина ряда.
Значения периодограммы можно интерпретировать как дисперсию (вариацию) данных на соответствующей частоте. Обычно периодограммы изображают в зависимости от частот или периодов.
Подготовка данных к анализу
Полезно вычесть среднее из значений ряда и удалить тренд (чтобы добиться стационарности) перед анализом. Оба этих эффекта могут заслонить более интересные периодичности в данных, поэтому и среднее, и (линейный) тренд следует удалить из ряда перед анализом. Иногда также полезно сгладить данные перед анализом, чтобы убрать случайный шум, который может засорять существенные периодические циклы в периодограмме.
Если повторяющихся циклов в данных нет, т.е. если каждое наблюдение совершенно независимо, то распределение наблюдений соответствует нормальному. Такой временной ряд называют «белым шумом».
Алгоритм быстрого преобразования Фурье (БПФ). Для нахождения параметров синусов и косинусов для ряда N из значений требуется как минимум N2 (комплексных) умножений (для 8,000 наблюдений потребовалось бы 64 миллиона умножений), число наблюдений может быть в десятки и сотни раз большим. Тогда даже в условиях современных высокоскоростных компьютеров с большой оперативной памятью использование алгоритма ВПФ [ ], сокращающего количество операций во много раз, может оказаться чрезвычайно эффективным.
Недостаток стандартного алгоритма БПФ состоит в том, что число данных ряда должно быть равным степени 2 (т.е. 16, 64, 128,...).
Кросс-спектральный анализ развивает одномерный спектральный анализ и позволяет анализировать одновременно два ряда. С первого взгляда нелегко рассмотреть взаимосвязь между двумя рядами. Но кросс-спектральный анализ позволяет установить, что ряды содержат две сильно коррелируемые периодичности. Кросс-спектр состоит из комплексных чисел, которые могут быть разделены на действительную и мнимую части.
Бывает очень важно определить, насколько каждая частотная компонента одного ряда, например технологического параметра, опережает частотные компоненты другого ряда, представляющего, например, характеристику качества готовой продукции.
