Методология работы в программе MS EXCEL с функциями нормального распределения и распределения Стьюдента

Функция НОРМРАСП(рис. 5.8) определяет плотность f и интегральную функцию F нормального распределения при заданных аргументах:

- «x» - значение X, для которого определяются значения f или F.

- «Среднее» - математическое ожидание (или его оценка), представленное самим значением или ссылкой на ячейку, содержащую результат его расчёта.

- «Стандартное откл» - стандартное отклонение распределения (или оценка стандартного отклонения) или ссылка на ячейку, содержащую результат его расчёта.

- «Интегральная» - см. § 2.3.

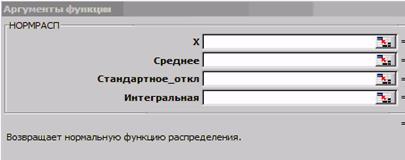
Рис. 5.8. Аргументы функции НОРМРАСП

Например, поставлена задача определения вероятности попадания некоторой характеристики (размера, какого-либо механического свойства и т.д.) в поле допуска с границами (x₁, x₂), если известна выборка значений этой характеристики. Тогда, подставляя в аргументы функции НОРМРАСП рассчитанные «Среднее» и «Стандартное откл», в «Интегральная» - значение ИСТИНА, а в «x» - последовательно x₁ и x_2, определяют интегральную функцию и для нижней и верхней границы поля допуска. Искомая вероятность представляет собой разность -

Функция НОРМСТРАСП определяет интегральное функцию стандартного нормального распределения. Эта функция используется вместо справочной таблицы для стандартной нормальной кривой (приложение ). Поскольку для стандартного нормального распределения 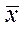=0 и σ=1 известны, в функции НОРМСТРАСП представлен лишь один аргумент - z.

НОРМОБР - функция, обратная функции НОРМРАСП, определяющей по заданному значению x интегральную функцию F. НОРМОБР (рис. 5.9) для указанного среднего и стандартного отклонения по заданному значению вероятности ищет значение x, используя метод итераций. (Такую же операцию выполняет функция НОРМСТОБР, но для стандартного нормального распределения.)

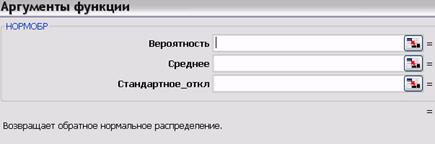
Рис. 5.9. Аргументы функции НОРМОБР

Функцию НОРМОБР удобно использовать для нахождения границ доверительного интервала, обеспечивающих необходимую вероятность попадания в этот интервал контролируемой характеристики. Для этого уровень значимости α, например 0,05, делят на две части, обычно пополам. Для нахождения нижней границы интервала в качестве аргумента «Вероятность» (см. рис. 5.9) ставят величину α/2 (= 0,025). Для определения верхней границы в качестве аргумента «Вероятность» ставят величину 1,0 - α/2 (= 0,975).

Но бывают случаи, когда выпады за пределы нижней и верхней границы доверительного интервала неравноценны по своим последствиям. Например, при изготовлении детали выпад в одну сторону от допуска может означать исправимый, а в другую - неисправимый брак. В этом случае по сравнению с предыдущим уровень значимости α, например 0,05, делят на две неравные части. Меньшую часть назначают в сторону области неисправимого брака (например, при обработке вала - в сторону меньших размеров). Наоборот, бóльшую часть α назначают в сторону исправимого брака, то есть при обработке вала в сторону бóльших размеров.

Таким образом, будучи родственной функции ДОВЕРИТ (см. ниже § 6.3), устанавливающей только ширину доверительного интервала, функция НОРМОБР имеет более широкие возможности в отношении установления расположения доверительного интервала, см. ниже § 6.6.

Функция СТЬЮДРАСП (рис. 5.10) определяет процентные точки (вероятность) для t-распределения Стьюдента, используемого для проверки гипотез при малом объеме выборки. При увеличении n оно приближается к нормальному распределению. (В аргументах функции СТЬЮДРАСП, как и в аргументах функции НОРМСТРАСПотсутствуют математическое ожидание и дисперсия.)

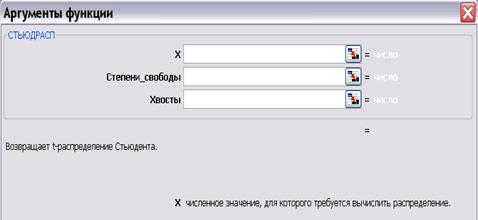
Рис. 5.10. Аргументы функции СТЬЮДРАСП

В качестве аргументов функции используются:

- «x» - это значение, для которого вычисляются вероятности;

- «Степени_свободы» - целое, указывающее число степеней свободы k;

- «Хвосты» - число, которое может быть равно 1 или 2 и определяет следующим образом характер распределения: если «Хвосты» = 1, то функция СТЬЮДРАСП определяет одностороннее распределение; если «Хвосты» = 2, то функция СТЬЮДРАСП определяет двухстороннее распределение.

Расчет производится только для x ³ 0. Но следует помнить, что для одностороннего распределения: СТЬЮДРАСП(-x,df,1) = 1 – СТЬЮДРАСП(x,df,1) и для двустороннего распределения: СТЬЮДРАСП(-x,df,2) = СТЬЮДРАСП(x df,2). То есть распределение Стьюдента можно «достроить» и для области x < 0.

Данную функцию можно использовать вместо таблицы критических значений t-распределения (Приложение ) для определения значений односторонней или двусторонней доверительной вероятности. Например, для t-распределения с числом степеней свободы k = 9 (выборка объёмом n = 10) для значения t = 2,262 (вставляется в «x») для одностороннего распределения («Хвосты» = 1) будет получен уровень значимости α = 0,025, а для двустороннего распределения («Хвосты» = 2) - уровень значимости α = 0,05 (см. приложение ).

Функция СТЬЮДРАСПОБР (рис. 5.11) в практике статистического анализа используется более часто, чем Функция СТЬЮДРАСП, т.к. определяет критическое значение t-распределения для заданных доверительной вероятности (соответствующей двустороннему распределению Стьюдента) и числа степеней свободы.

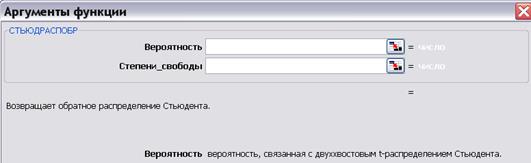
Рис. 5.11. Аргументы функции СТЬЮДРАСПОБР

Таким образом, при использовании функции СТЬЮДРАСПОБР для заданного уровня значимости α = 0,05 и числа степеней свободы k = 9 получается заданное ранее (см. выше) двустороннее t-значение 2,262 (см. также приложение ).

При необходимости установления одностороннего t-значения оно может быть получено при замене аргумента «Вероятность» на удвоенное (2*α) значение. В результате подстановки в аргумент «Вероятность» значения 0,1=2*0,05 для того же числа степеней свободы k=9 получается одностороннее t-значение, равное 1,833.