Нормальное и стандартное нормальное распределения
Из непрерывных распределений наиболее распространённым в технике и занимающим, поэтому особое положение является нормальное распределение или распределение Гаусса. Это позволяет исследователям и технологам во многих случаях априори при осуществлении анализов с определённой степенью достоверности предполагать выполнение этого закона без проведения специальных исследований.
Пусть случайная величина X имеет нормальное распределение с произвольными параметрами µ (центр распределения, математическое ожидание) и 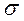 (стандартное отклонение). В этом случае функция плотности распределения (f) и интегральная функция (F) представлены соответственно формулами (5.1) и (5.2), а графики этих функций - на рис. 5.1.
(стандартное отклонение). В этом случае функция плотности распределения (f) и интегральная функция (F) представлены соответственно формулами (5.1) и (5.2), а графики этих функций - на рис. 5.1.
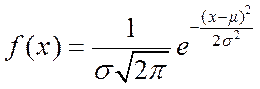 (5.1)
(5.1)
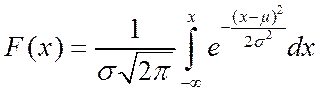 (5.2)
(5.2)
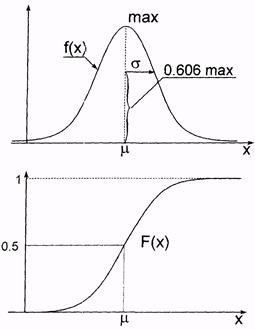
Рис. 5.1. Функция плотности (f) с указанным значением максимальной плотности ( 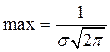 ) и соответствующая интегральная функция (F) нормального распределения
) и соответствующая интегральная функция (F) нормального распределения
Применительно к выборке функция плотности и интегральная функция распределения записываются соответственно формулами (5.3-5.4), где µ и 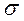 заменены их выборочными точечными оценками, соответственно
заменены их выборочными точечными оценками, соответственно 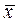 и SX:
и SX:
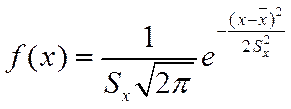 . (5.3)
. (5.3)
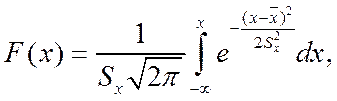 . (5.4)
. (5.4)
При этом область значений функций - вся числовая ось -∞ < x < ∞.
Доли интегральной функции нормального распределения в обе стороны от математического ожидания на расстояния кратные стандартному отклонению приведены на рис. 5.2.
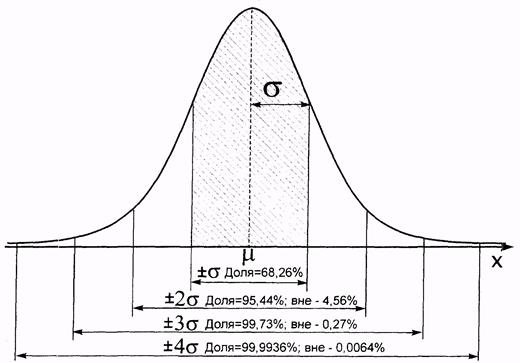
Рис. 5.2. Значения интегральной функции нормального распределения в областях кратных σ, окружающих математическое ожидание
«Стандартное нормальное распределение» отличается от других распределений этого типа тем, что в нём µ = 0 и σ = 1. В этом случае формулы (5.3) и (5.4) преобразуются соответственно в (5.5) и (5.6).
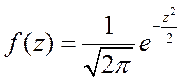 (5.5)
(5.5)
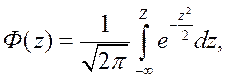 (5.6)
(5.6)
Стандартное нормальное распределение имеет особое значение, т.к. именно для него составлены справочные таблицы. В результате значения f и F можно получать из таблиц, не рассчитывая их по достаточно сложным формулам (5.5-5.6). В справочной таблице приводятся значения интегральной функции F(z), которая для стандартного нормального закона распределения обычно обозначается Ф(z) (5.6), т.е. значения площади (заштрихована, рис. 5.3) под кривой плотности стандартного нормального закона распределения f(z), определяемой формулой (5.5). Видно, что площадь Ф(z) под кривой f(z) определяется левее заданной точки z0; эта площадь численно равна вероятности того, что стандартная нормальная случайная величина Z не превосходит заданного значения z0.
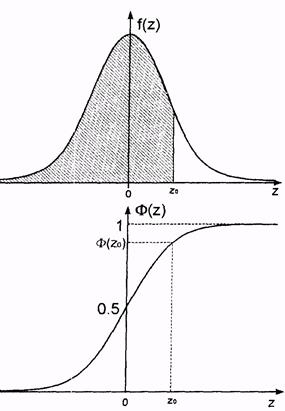
Рис. 5.3. Графики плотности и интегральной функции "стандартного нормального распределения".
Как правило, технолог или исследователь анализирует нормальное распределение с произвольными величинами µ и σ. Поэтому для решения практических задач пользуются так называемыми «преобразованиями подобия» (5.7), позволяющими осуществлять переход от произвольного нормального распределения X к стандартному нормальному распределению Z и наоборот.
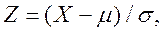
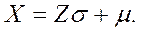 (5.7)
(5.7)
Обычно для вычисления долей в пространстве X (случайная величина, распределённая по нормальному закону с произвольными параметрами µ и σ) эти доли определяются в пространстве Z (случайная величина со стандартным нормальным распределением), используя табулированные (справочные, табличные) значения функции Ф(z). Затем, используя второе преобразование, переходят от пространства Z к пространству X.
Следует отметить, что работа с рассмотренными в § 5.4 (см. ниже) функциями MS EXCEL для определения плотности распределения f(x) и интегральной функции F(x) не только нормального, но и многих других распределений не требует не только каких-либо вычислений, но и обращения к справочным данным.
