Тема: «Числовые головоломки»
Цель: развивать умения учащихся представлять данное число с помощью нескольких одинаковых чисел и с помощью действий сложения, умножения, вычитания, деления или их комбинации.
1.Устные решения задач.
1) Определить арифметическое действие, с помощью которого из двух крайних чисел получено среднее, и вместо знака «?» вставить пропущенное число.
42(47)5 6(66)11 36(25)11 48(4)12
31(?)8 5(?)12 48(?)12 100(?)5
Ответ: 39, 60, 36, 20.
2) Требуется распилить бревно на 6 частей. Каждый распил занимает 2 минуты. Сколько времени потребуется на эту работу?
Ответ: 10 минут.
3) Сколькими способами можно уплатить без сдачи 28 копеек, имея только монеты 1-и 5- копеечного достоинства?
2.Задачи и упражнения.
1. Запишите, пользуясь тремя пятёрками и знаками действий: 1) 2, 2) 5.
2. Пользуясь пятью двойками и знаками действий, запишите число 28.
3. Пользуясь четырьмя двойками и знаками действий, запишите число 111.
4. Запишите число 100, пользуясь знаком «+» и: 1)четырьмя девятками, 2) шестью девятками (Допускается использование дробной черты.)
5. Запишите число 31, пользуясь знаками действий и: 1) пятью тройками, 2) шестью тройками, 3) пятью пятёрками.
6. Запишите число 100, пользуясь знаками действий и: 1) пятью единицами, 2) пятью тройками, 3) пятью пятёрками.
7.Напишите, пользуясь двумя цифрами и знаками действий, возможно меньшее число.
8. С помощью четырёх четвёрок и известных вам знаков действий запишите все натуральные числа от1 до 9.
9.Можно ли 5 яблок разделить между 6 мальчиками поровну, так чтобы не пришлось ни одного яблока резать больше чем на 3 части?
10.Как 7 яблок разделить поровну между 12 мальчиками, не разрезая ни одного яблока больше, чем на 4 части?
11.Поместите девять знаков плюс и минус между цифрами так, чтобы получилось верное выражение 0 1 2 3 4 5 6 7 8 9 = 1.
Ответ
1) 1. (5+5):5 2) 22+2+2+2 3) 2222 4) 99+9׃9
2. 5∙5׃5
5) 1) 33-(3+3)׃3 2) 3∙3∙3+3+3׃3 3) 5∙5+5+5׃5
6) 1) 111-11 2) 33∙3+3׃3 3) 5∙5∙5-5∙5
8)
| 4+4 | ; | + | ; | 4+4+4 | ; | 4*4+4 | ; | 4+(4-4)*4; | 4+4 | +4; | 4+4- | ; | (4+4)*4 | ; 4+4+ | ||||
| 4+4 |
9) Каждый должен получить 5/6 яблока, но 5/6=1/2+1/3. 3 яблока нужно разрезать пополам и 2 яблока – каждое на три равные части.
10) 7/12=1/3+1/4
11) 0 + 1 + 2 - 3 - 4 + 5 + 6 - 7 - 8 + 9 = 1
Математический бой.
Цель:Привитие интереса к занятиям математики, обучение учащихся навыкам самостоятельного решения сложных нестандартных задач, развитие критичности мышления.
Ученики разбиваются на две команды. Даётся 20 минут на решение блока задач, каждое задание 6 баллов.
Блок задач, предложенный к решению. (Без решений)
1. Напишите девять цифр: 1 2 3 4 5 6 7 8 9. Не меняя порядка этих цифр, расставьте между ними плюсы и минусы, всего три знака, таким образом, чтобы в результате получилось 100.
2. Запишите число 100, использовав все 10 цифр и знаки некоторых действий.
11.Какие знаки арифметических действий нужно поставить между восемью двойками, записанными одна за другой, чтобы результат этих действий был равен 8?
3. 1)Как нужно расставить знаки «+» в записи 1 2 3 4 5 6 7 , чтобы получилась сумма, равная 100?
2) Как нужно расставить знаки «+» в записи 9 8 7 6 5 4 3 2 1, чтобы получилась сумма, равная 99?
4. 1)Сумма, каких двух натуральных чисел равна их произведению?
2)Сумма, каких двух натуральных чисел больше, чем их произведение?
Как нужно разрезать циферблат часов на 6 частей так, чтобы во всех частях сумма чисел была одинакова?
По окончании времени, проводится конкурс капитанов, для определения первого, кто бросит вызов.
Из шести спичек построить четыре равносторонних треугольника на плоскости.
Далее бой проходит согласно правилам, указанным в приложении.
Домашнее задание
1) Когда молчаливого и задумчивого Оксфордского студента, которому "милее двадцать книг иметь, чем платье дорогое, лютню, снедь", убедили задать головоломку своим сотоварищам по путешествию, он сказал:
- Я тут как-то размышлял над теми странными и таинственными талисманами, охраняющими от чумы и прочих зол, в которых замешаны магические квадраты. Глубока тайна подобных вещей, а числа таких квадратов воистину можно назвать великими. Но та небольшая загадка, которую я придумал накануне для всей компании, не настолько трудна, чтобы ее нельзя было решить, вооружившись ненадолго терпением.
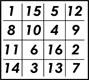
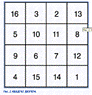
Затем студент изобразил квадрат, показанный на рисунке, и сказал, что его надо разрезать на четыре части (вдоль прямых), которые можно было бы сложить заново так, чтобы при этом получился правильный магический квадрат. У такого квадрата сумма чисел, стоящих в каждой строке, столбце и на каждой из двух больших диагоналей, равна 34. Эта головоломка для большинства читателей окажется нетрудной.
Ответ
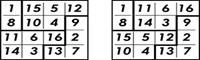
На рисунке показано, как именно следует разрезать квадрат на четыре части и как из них сложить магический квадрат. Можно проверить, что сумма чисел в каждой строке, столбце и на каждой диагонали равна 34.
2)Головоломка Мельника.Теперь очередь была за Мельником. Этот "ражий малый, костистый, узловатый и бывалый" отвел компанию в сторону и показал девять мешков с зерном, которые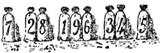 
стояли, как показано на рисунке.- Слушайте и внемлите, - сказал он, - я загадаю вам загадку про эти мешки пшеницы. И заметьте, господа хорошие, что сбоку стоит по одному мешку, затем идут пары мешков, а посредине вы видите три мешка. Клянусь святым Бенедиктом, получилось так, что если мы умножим пару, 28, на один мешок, 7, то получится 196, что и указано на средних мешках. Но если вы умножите другую пару, 34, на ее соседа, 5, то не получите при этом 196. Теперь я прошу вас, добрые господа, переставить эти девять мешков, как можно меньше надрываясь, так, чтобы каждая пара, умноженная на своего соседа, давала число, стоящее в середине. Поскольку условием Мельника было передвигать как можно меньшее число мешков, у данной головоломки только один ответ, который, вероятно, каждый сумеет найти.
Ответ. Нужно разместить мешки следующим образом: 2, 78, 156, 39, 4. Здесь каждая пара, умноженная на своего единственного соседа, дает число, стоящее в середине, причем пришлось передвинуть пять мешков. Существует лишь три других расположения мешков (4, 39, 156, 78, 2; или З, 58, 174, 29, 6; или б, 29, 174, 58, 3), но при этом требуется передвинуть семь мешков.
Приложение 5
Математические карусели
Это командное соревнование по решению задач. Побеждает в нём команда, набравшая наибольшее число очков. Задачи решаются на двух рубежах – исходном и зачётном. Очки начисляются только за задачи, решённые на зачётном рубеже. В начале игры все члены команды располагаются на исходном рубеже, причём им присвоены номера от 1 до 6. По сигналу ведущего команды получают задачу и начинают её решать. Если команда считает, что задача решена, её представитель, имеющий номер 1, предъявляет решение судье. Если оно верное, игрок № 1 переходит на зачётный рубеж и получает задачу там, а члены команды, оставшиеся на исходном рубеже, тоже получают новую задачу. В дальнейшем члены команды, находящиеся на исходном и зачётном рубежах, решают разные задачи независимо друг от друга.
Если решение правильное, то с исходного рубежа этот игрок переходит на зачётный, а на зачётном возвращается на своё место в очереди. Если решение неправильное, то на исходном рубеже игрок возвращается на свое место в очереди, а с зачётного рубежа переходит на исходный. Игрок, перешедший с одного рубежа на другой, становится в конец очереди. И на исходном и на зачётном рубежах команда может в любой момент отказаться отрешения задачи. При этом задача считается нерешённой.
После того как часть команды, находящаяся на каком-либо из двух рубежей, рассказала решение очередной задачи или отказалась её решать дальше, она получает новую задачу. Если на рубеже в этот момент нет ни одного участника, задача начинает решаться тогда, когда этот участник там появляется.
За первую верно решённую на зачётном рубеже задачу команда получает 3 балла. Если команда на зачётном рубеже верно решает несколько задач подряд, то за каждую следующую задачу она получает на 1 балл больше, чем за предыдущую. Если же очередная задача решена неверно, то цена следующей задачи зависит от её цены следующим образом. Если цена неверно решённой задачи была больше 6 баллов, то следующая задача стоит 5 баллов. Если же неверно решённая задача стоила 3 балла, то следующая задача тоже стоит 3 балла.
Игра для команды оканчивается, а) кончилось время, или
б) кончились задачи на зачётном рубеже, или
в) кончились задачи на исходном рубеже, а на зачётном рубеже нет ни одного игрока.
Время игры, количество исходных и зачётных задач заранее оговариваются.
Игра оканчивается, если она закончилась для всех команд.
(Может быть и мини-карусель, если не предъявлять задач на исходном рубеже).
Приложение 6
Тема: «Магические квадраты»
Цель:Историческая справка о возникновении магических квадратов, развитие у учащихся интереса к истории математики. Научиться решать и составлять магические квадраты.
1.Беседа учителя
МАГИЧЕСКИЙ КВАДРАТ,квадратная таблица из целых чисел, в которой суммы чисел вдоль любой строки, любого столбца и любой из двух главных диагоналей равны одному и тому же числу.
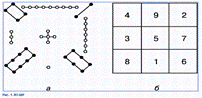
Магический квадрат – древнекитайского происхождения. Согласно легенде, во времена правления императора Ю (ок. 2200 до н.э.) из вод Хуанхэ (Желтой реки) всплыла священная черепаха, на панцире которой были начертаны таинственные иероглифы (рис. 1,а), и эти знаки известны под названием ло-шу и равносильны магическому квадрату, изображенному на рис. 1,б. В 11 в. о магических квадратах узнали в Индии, а затем в Японии, где в 16 в. магическим квадратам была посвящена обширная литература. Европейцев с магическими квадратами познакомил в 15 в. византийский писатель Э.Мосхопулос. Первым квадратом, придуманным европейцем, считается квадрат А.Дюрера (рис. 2), изображенный на его знаменитой гравюре Меланхолия 1. Дата создания гравюры (1514) указана числами, стоящими в двух центральных клетках нижней строки. Магическим квадратам приписывали различные мистические свойства. В 16 в. Корнелий Генрих Агриппа построил квадраты 3-го, 4-го, 5-го, 6-го, 7-го, 8-го и 9-го порядков, которые были связаны с астрологией 7 планет. Бытовало поверье, что выгравированный на серебре магический квадрат защищает от чумы. Даже сегодня среди атрибутов европейских прорицателей можно увидеть магические квадраты.
Великие ученые древности считали количественные отношения основой сущности мира. Поэтому числа и их соотношения занимали величайшие умы человечества. «В дни моей юности я в свободное время развлекался тем, что составлял… магические квадраты»- писал Бенджамин Франклин. Магический квадрат- это квадрат, сумма чисел которого в каждом горизонтальном ряду, в каждом вертикальном ряду и по каждой из диагоналей одна и та же.
Некоторые выдающиеся математики посвятили свои работы магическим квадратам и полученные ими результаты оказали влияние на развитие групп, структур, латинских квадратов, определителей, разбиений, матриц, сравнений и других нетривиальных разделов математики.
Полного описания всех возможных магических квадратов не получено и до сего времени. Магических квадратов 2х2 не существует. Существует единственный магический квадрат 3х3, так как остальные магические квадраты 3х3 получаются из него либо поворотом вокруг центра, либо отражением относительно одной из его осей симметрии.
Расположить натуральные числа от 1 до 9 в магический квадрат 3х3 можно 8 различными способами:
9+5+1
9+4+2
8+6+2
8+5+2
8+4+3
7+6+2
7+5+3
6+5+4
В магическом квадрате 3х3 магической постоянной 15 должны быть равны сумме трех чисел по 8 направлениям: по 3 строкам, 3 столбцам и 2 диагоналям. Так как число, стоящее в центре, принадлежит 1 строке, 1 столбцу и 2 диагоналям, оно входит в 4 из 8 троек, дающих в сумме магическую постоянную. Такое число только одно: это 5. Следовательно, число, стоящее в центре магического квадрата 3х3, уже известно: оно равно 5.
Рассмотрим число 9. Оно входит только в 2 тройки чисел. Мы не можем поместить его в угол, так как каждая угловая клетка принадлежит 3 тройкам: строке, столбцу и диагонали. Следовательно, число 9 должно стоять в какой–то клетке, примыкающей к стороне квадрата в ее середине. Из-за симметрии квадрата безразлично, какую из сторон мы выберем, поэтому пишем 9 над числом 5, стоящим в центральной клетке. По обе стороны от девятки в верхней строке мы можем вписать только числа 2 и 4. Какое из этих двух чисел окажется в правом верхнем углу и какое в левом, опять – таки не имеет значения, так как одно расположение чисел переходит в другое при зеркальном отражении. Остальные клетки заполняются автоматически. Проведенное нами простое построение магического квадрата 3х3 доказывает его единственность.
Такой магический квадрат был у древних китайцев символом огромного значения. Цифра 5 в середине означала землю, а вокруг нее в строгом равновесии располагались огонь (2 и 7), вода (1 и 6),
дерево (3 и 8), металл (4 и 9).
1.Решение задач.
1) Проверьте основные свойства магического квадрата Дюрера, посчитав суммы по строкам, столбцам и диагоналям. Исследуйте другие свойства этого квадрата, посчитав сумму чисел центрального квадрата и каждого из угловых квадратов.
2) Возьмите квадрат 4х4 впишите в него числа от1 до 16 по порядку. Теперь поменяйте местами числа, стоящие в противоположных углах центрального квадрата. Если вы всё сделали правильно, то должен получиться магический квадрат. Проверьте.
3) Квадрат разделен на 9 равных клеток. Расставьте в этих клетках числа 1, 2, 3, 4, 5, 6, 7, 8, 9 так, чтобы сумма чисел в каждой строке и в каждом столбике равнялась 15.
Решение.
Так как сумма всех однозначных чисел 45, то решение задачи возможно (строк 3 и столбиков 3). При решении задачи используем представление числа 15 в виде суммы трех однозначных чисел.
Ответ.
4)Составьте все 8 различных магических квадратов из чисел от 1 до 9.
5) Разместите в свободных клетках квадрата еще числа 3, 4, 5, 6, 7, 8, 9 так, чтобы по любой вертикали, горизонтали и диагонали получилось в сумме одно и то же число:
Ответ.
6) Даны числа: 5, 10, 15, 20, 25, 30, 35, 40, 45.
Впишите их в клетки девяти клеточного квадрата так, чтобы получилось в сумме одно и то же число по любой вертикали, горизонтали и диагонали.
Ответ.
7) В клетках квадрата переставьте числа так, чтобы по любой вертикали, горизонтали и диагонали их суммы были равны между собой:
Ответ.
Приложение 7