Векторное произведение векторов. Различные подходы к введению понятия вектора в основной школе.

Вектор называется векторным произведением неколлинеарных векторов и , если:

1) его длина равна произведению длин векторов и на синус угла между ними: = φ

2) вектор ортогонален векторам и ;

3) тройки векторов ( ) и , , ) ориентированы одинаково.

Векторное произведение коллинеарных векторов (в частности, если хотя бы один из множителей — нулевой вектор) считается равным нулевому вектору.

Векторное произведение обозначается =[ , ] или × .

Свойства векторного произведения векторов:

1⁰. × = - (антикоммутативный закон);

2⁰. ( ) = = ( × );

3⁰. ( + ) = + , + )= + + (дистрибутивный закон относительно сложения);

4⁰. = для любого вектора

Док-во 1⁰: Пусть × , 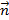=- . Если векторы и коллинеарны, то в силу коллинеарности векторов = и св-во док-но. Если же и не коллинеарны, то векторы , во-первых, имеют одинаковую длину и, во-вторых, коллинеарны (в силу того, что оба вектора ортогональны к плоскости, определяемой векторами и ). Но тогда либо , либо . Если бы имела место первая возможность, то по определению векторного произведения обе тройки и оказались бы правыми, но это невозможно (ибо эти тройки противоположной ориентации). Итак, и св-во док-но.

Док-во 2⁰: Пусть , 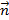= ) и исключим тривиальные случаи, когда вектор коллинеарен или когда 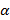=0. В этих случаях (в силу НДУ коллинеарности векторов и определения произведения вектора на число) получаем, что = , и св-во 2 док-но.

Если векторы и не коллинеарны и 0. Докажем, что и в этом случае векторы равны. |Обозначим угол между векторами и через , а угол между векторами и через ψ. По опр. векторного произведения и произведения вектора можно утверждать, что = * , = * (1).

Могут быть два случая: 1) ψ=φ (когда α>0 и векторы и направлены в одну сторону); 2) ψ=π-φ (когда α<0 и векторы и направлены в противоположные стороны). В обоих случаях sinψ=sinφи в силу формул (1) = , т.е. векторы имеют одинаковую длину.

Далее, очевидно, что векторы коллинеарны, ибо ортогональность к плоскости, определяемой векторами и , означает ортогональность и плоскости, определяемой векторами и Для док-ва равенства векторов остается проверить, что эти векторы имеют одинаковое направление. Пусть α>0 (α<0); тогда векторы и одинаково направлены (противоположно направлены), и, стало быть, векторы и ) также одинаково направлены (противоположно направлены), а это означает, что векторы , 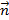= ) всегда одинаково направлены. Св-во доказано.

Док-во 3⁰: Если вектор единичный и ему ортогонален, то вектор получится, если повернуть в плоскости, перпендикулярной , на прямой угол в таком направлении, чтобы он образовал с правую тройку.

Док-во 4⁰: Это св-во непосредственно следует из НДУ коллинеарности векторов и из того, что любой вектор коллинеарен сам с собой.

НДУ коллинеарности векторов: || ó = .

Док-во: 1) Необходимость вытекает из самого определения векторного произведения: для коллинеарных векторов и векторное произведение по определению рано нулю.

2) Достаточность. Пусть векторное произведение = . Докажем, что векторы и коллинеарны.

Прежде всего, исключим тривиальный случай, когда хотя бы один из векторов и является нулевым (нулевой вектор имеет неопределенное направление, и его можно считать коллинеарным любому вектору). Если же оба вектора и ненулевые, то >0 и >0, и поэтому из равенства = , т.е. векторы и коллинеарны, ч.т.д.

Вычисление векторного произведения векторов, заданных координатами в ортогональном базисе.

Т1. Если два вектора и определены своими декартовыми прямоугольными координатами (a₁, a₂, a₃), (b₁, b₂, b₃), то координаты векторного произведения вычисляются по формуле:

= .

Док-во: Так как векторы и определены своими декартовыми прямоугольными координатами, то имеем:

=(a₂b₃ – b₂a₃, -a₁b₃ + b₁a₃, a₁b₂ – b₁a₂)= .

Замечание. Формулу приведенную в теореме можно записать иначе:

= .

Приложение векторного произведения к вычислению площади треугольника.

Задача. Найти площадь треугольника ABC, если в некоторой прямоугольной системе координат даны координаты его вершин:A(x₁,y₁,z₁), B(x₂,y₂,z₂), C(x₃,y₃,z₃).

Решение. Площадь параллелограмма, построенного на векторах , , численно равна . Отсюдаследует, что .

Векторы , имеют координаты (x₂-x₁, y₂-y₁, z₂-z₁), (x₃-x₁, y₃-y₁, z₃-z₁), поэтому, используя формулу площади получаем:

В частности, если вершины треугольника лежат в плоскости Oxy, то z₁=z₂=z₃=0, поэтому .

В учебной литературе и практике обучения математике существуют различные подходы к определению понятия вектора. В большинстве учебных курсов вектор определяется как направленный отрезок. При этой трактовке векторы считаются равными, если они имеют одинаковую длину и направление. Несмотря на широкую распространенность этого определения, его нельзя признать математически корректным, хотя бы в силу определения равенства.

В самом деле, «равные векторы» - это по существу «один и тот же вектор» (аналогично тому, как «равные числа» - по существу «одно и то же число»), тогда как направленные отрезки AB и CD – это различные отрезки, а не один и тот же отрезок. Тем самым, приняв это определение вектора, мы отождествляем два различных (хотя и родственных) математических понятия: понятие равенства и эквивалентности.

Иногда вектор определяют как упорядоченную пару точек; однако сразу же, как правило, переходят к более наглядному его толкованию как направленного отрезка. Трудность выбора того или иного определения вектора возникает и потому, что в различных научных дисциплинах используются различные виды векторов. Так, в механике обычно рассматриваются так называемые скользящие векторы (вектор, начало которого можно выбирать на некоторой прямой, по которой он может перемещаться) и связанный вектор (вектор, начало которого отождествляется с некоторой фиксированной точкой); в математике же обычно имеют дело с так называемым свободным вектором (не связанным ни с какой прямой и ни с какой фиксированной точкой).

В учебниках Погорелова Атанасяна, Шарыгина вектор отождествляется с направленным отрезком. Равенство же векторов определяется по-разному: Атанасян, Шарыгин – одинаковая длина и направление; Погорелов – совмещение параллельным переносом.