Глава 1.Введение в математический анализ.

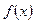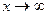Определение 1. Пределом функции при называется число b, если для любого 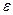( 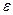– сколь угодно малое положительное число) можно найти такое значение аргумента 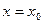, начиная с которого выполняется неравенство .

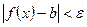Обозначение: .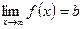

Определение 2. Пределом функци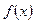и при 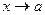называется число b, если для любого 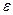( 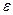- сколь угодно малое положительное число) существует такое положительное число 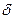, что для всех значений x, удовлетворяющих неравенству 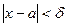выполняется неравенство .

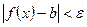Обозначение: .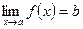

Теоремы о пределах.

1. Функция не может иметь более одного предела.

2. Предел алгебраической суммы нескольких функций равен алгебраической сумме пределов этих функций:

.

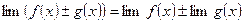3. Предел произведения нескольких функций равен произведению пределов этих функций:

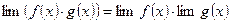
4. Предел степени равен степени предела:

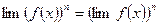
5. Предел частного равен частному пределов, если предел делителя существует:

.

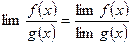6. Первый замечательный предел. .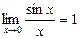

Следствия: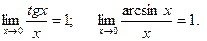

7. Второй замечательный предел:

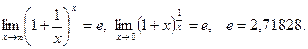
Следствия: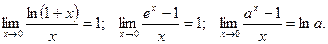

Бесконечно малые и бесконечно большие величины.

Определение 3. Функция 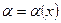называется бесконечно малой пр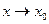и или 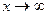, ес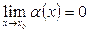ли или .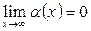

Свойства.

1. Алгебраическая сумма конечного числа бесконечно малых величин есть величина бесконечно малая.
2. Произведение бесконечно малой величины на ограниченную функцию (постоянную, другую бесконечно малую величину.) есть величина бесконечно малая.
3. Частное от деления бесконечно малой величины на функцию, предел которой отличен от нуля, есть величина бесконечно малая.

Определение 4. Функция 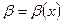называется бесконечно большой при 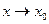, если .

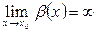Свойства.

1. Произведение бесконечно большой величины на функцию, предел которой отличен от нуля, есть величина бесконечно большая.
2. Сумма бесконечно большой величины и ограниченной функции есть величина бесконечно большая.
3. Частное от деления бесконечно большой величины на функцию, имеющую предел, есть величина бесконечно большая.

Теорема. (Связь между бесконечно малой величиной и бесконечно большой величиной) Если функция 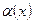бесконечно малая при 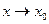( 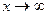), то функция 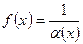является бесконечно большой величиной при 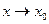( 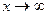). И, обратно, если функция 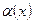бесконечно большая при 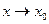( 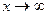), то функция 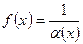является бесконечно малой величиной при ( ).

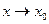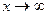Эквивалентные бесконечно малые величины при :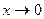

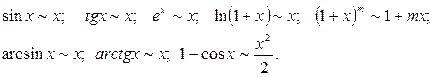
Вычисление пределов.

При вычислении пределов используют основные теоремы о пределах, свойства непрерывных функций и правила, вытекающие из этих теорем и свойств.

Правило 1. Чтобы найти предел в точке 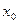функции, непрерывной в этой точке, надо в функцию, стоящую под знаком предела, вместо аргумента x подставить его предельное значение .

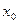Пример 1. Найти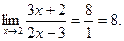

Правило 2. Если при отыскании предела дроби предел знаменателя равен нулю, а предел числителя отличен от нуля, то предел такой функции равен .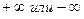

Пример 2. Найти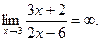

Правило 3. Если при отыскании предела дроби предел знаменателя равен 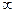, а предел числителя отличен от нуля, то предел такой функции равен нулю.

Пример 3. Найти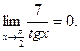

Часто подстановка предельного значения аргумента приводит к неопределенным выражениям вида

.

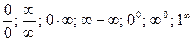Нахождение предела функции в этих случаях называется раскрытием неопределенности.

Правило 4. Неопределенность вида 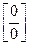раскрывается путем преобразования подпредельной функции т.о., чтобы в числителе и знаменателе выделить множитель, предел которого равен нулю, и, сократив на него дробь, найти предел частного. Для этого числитель и знаменатель либо раскладывают на множители, либо домножают на сопряженные числителю и знаменателю выражения.

Пример 4.

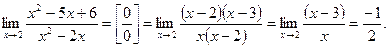
Пример 5. =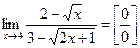

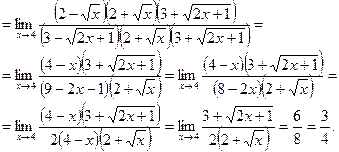
Правило 5. Если подпредельное выражение содержит тригонометрические функции, тогда, чтобы раскрыть неопределенность вида 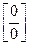используют первый замечательный предел.

Пример 6.

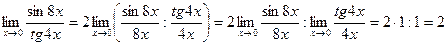Пример 7.

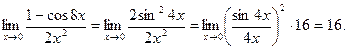
Правило 6. Чтобы раскрыть неопределенность вида 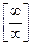при 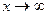, числитель и знаменатель подпредельной дроби необходимо разделить на высшую степень аргумента и находить далее предел частного.

Возможны результаты:

1) искомый предел равен отношению коэффициентов при старших степенях аргумента числителя и знаменателя, если эти степени одинаковы;

2) предел равен бесконечности, если степень аргумента числителя выше степени аргумента знаменателя;

3) предел равен нулю, если степень аргумента числителя ниже степени аргумента знаменателя.

Пример 8.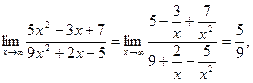

т.к.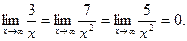

Пример 9.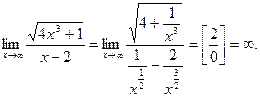

Пример 10.

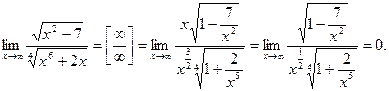
Можно было сразу сравнить степени аргумента числителя и знаменателя.

Пример 8. Степени равны, значит, предел равен отношению коэффициентов при старших степенях, т.е. .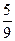

Пример 9. Степень числителя 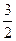, знаменателя – 1, значит, предел равен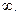

Пример 10. Степень числителя 1, знаменателя – 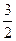, значит, предел равен 0.

Правило 7. Чтобы раскрыть неопределенность вида 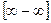, числитель и знаменатель подпредельной дроби необходимо домножить на сопряженное выражение.

Пример 11.

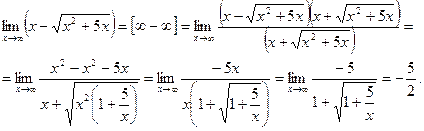
Правило 8. Чтобы раскрыть неопределенность вида 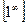используют второй замечательный предел и его следствия.

Можно доказать, что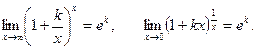

Пример 12.

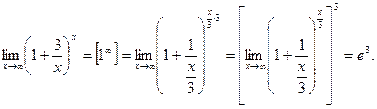
Пример 13. 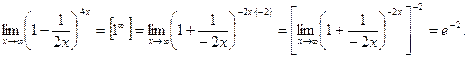Пример 14.

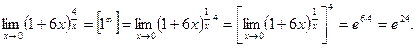
Правило 9. При раскрытии неопределенностей, подпредельная функция которых содержит б.м.в., необходимо заменить пределы этих б.м. на пределы б.м., эквивалентных им.

Пример 15.

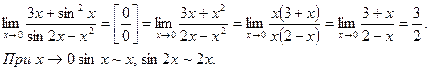
Пример 16.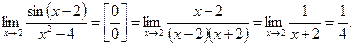

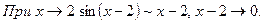
Правило 10. Правило Лопиталя (см. главу 2, с. 39).