Введение в математический анализ
Математический анализ
Методические указания по изучению дисциплины и задания для выполнения контрольной работы студентами-заочниками по специальности:
Нижний Тагил
Халтурина Т.Ю. Математический анализ.Методические указания.
Рецензент:
Утверждены на заседании кафедры
Протокол № _____ от _____________200 __ г.
Утверждены учебно-методическим советом
Протокол № _____ от _____________200 __ г.
Введение.
Курс математики дает основные определения, понятия и методы современной математики, которые лежат в основе изучения многих предметов экономического факультета. Любой курс современной экономики использует математический аппарат: анализируются графики различных зависимостей, проводится математическая обработка различных данных и т.д. Поэтому студенты должны знать основные определения и понятия, иметь навыки формализации задач и применения математических методов для подведения результатов вычислений и исследований.
1. Общие методические рекомендации.
Основной формой обучения студента – заочника является самостоятельная работа над учебным материалом: чтение учебников, решение задач, выполнение контрольных заданий. При самостоятельном изучении дисциплины вначале нужно ознакомиться с ее программой. Изучить материал, изложенный в рекомендуемой литературе. При этом следует составить краткий конспект из основных положений. Ответить на вопросы для самоконтроля. После усвоения учебного материала выполняется контрольная работа.
Программа курса
Элементы теории множеств.
Понятие множества. Операции над множествами. Числовые множества и их свойства. Числовая прямая (числовая ось) и множества на ней. Границы числовых множеств. Понятие окрестности точки. Точечные множества в N-мерном пространстве.
Вопросы для самоконтроля.
1. Дать понятие множества.
2. Способы задания множеств.
3. Объединение, пересечение, разность и симметрическая разность множеств.
4. Понятие окрестности точки.
Введение в математический анализ
Понятие функции. Свойства функций. Свойства и графики основных элементарных функций. Числовые последовательности и их свойства. Предел последовательности. Предел функции. Основные теоремы о пределах. Непрерывность функций. Глобальные свойства непрерывных функций.
Вопросы для самоконтроля.
5. Дать понятие функции, ее области определения и области значения.
6. Перечислить основные элементарные функции и их основные свойства и графики.
7. Дать определение предела числовой последовательности и предела функции. Написать основные свойства пределов.
8. Основные теоремы о пределах.
9. Раскрытие неопределенностей при вычислении пределов.
10. Использование первого и второго замечательных пределов при вычислении пределов.
11. Непрерывность функции в точке и на интервале. Точки разрыва функции.
Дифференциальное исчисление функции нескольких переменных.
Определение функции нескольких переменных. Предел и не прерывность функции нескольких переменных. Частные производные функции нескольких переменных, их геометрический смысл (для случая двух независимых переменных). Частные производные высших порядков. Полный дифференциал функции нескольких переменных, его применение в приближенных вычислениях. Экстремум функции нескольких переменных. Нахождение наибольшего и наименьшего значений.
Классические методы оптимизации. Функции спроса и предложения. Функции полезности. Кривые безразличия.
Вопросы для самоконтроля.
23. Дать определения функции двух переменных. Что является областью функции двух переменных.
24. Дать определения частных производных первого порядка функции двух переменных.
25. Нахождение частных производных второго порядка функции двух переменных.
26. Полный дифференциал функции нескольких переменных, его применение в приближенных вычислениях.
27. Экстремум функции нескольких переменных.
28. Нахождение наибольшего и наименьшего значений.
29. Функции спроса и предложения.
30. Функции полезности.
31. Кривые безразличия.
Интегральное исчисление.
Понятие первообразной функции и неопределенного интеграла. Основные свойства неопределенного интеграла. Таблица основных интегралов. Основные методы интегрирования: непосредственное интегрирование, подведение под знак дифференциала, замена переменной, интегрирование по частям. Интегрирование простейших рациональных дробей. Интегрирование некоторых видов иррациональностей. Интегрирование тригонометрических функций. Понятие определенного интеграла. Его геометрический и экономический смысл. Основные свойства определенного интеграла. Формула Ньютона-Лейбница для вычисления определенного интеграла. Замена переменной и интегрирование по частям в определенном интеграле. Несобственные интегралы. Применение определенного интеграла в экономике.
Вопросы для самоконтроля.
32. Дать определения неопределенного интеграла и перечислить его основные свойства.
33. Основные методы интегрирования (замена переменных, интегрирование по частям, подведения под знак дифференциала).
34. Понятие определенного интеграла.
35. Геометрический и экономический смысл определенного интеграла.
36. Формула Ньютона-Лейбница.
37. Замена переменных в определенном интеграле.
38. Интегрирование по частям в определенном интеграле.
39. Несобственные интегралы.
Задания к контрольной работе.
Контрольная работа должна быть выполнена в соответствии с вариантом, выбираемым по последней цифре номера зачетной книжки. При этом, если предпоследняя цифра учебного шифра нечетная (1, 3, 5, 7, 9), то номера заданий для соответствующего варианта даны в таблице 1. Если предпоследняя цифра четная или нуль (2, 4, 6, 8, 0), то номера задач даны в таблице 2. Каждая задача должна содержать условие, подробное решение и ответ.
Таблица 1
| № варианта | Номер задачи контрольной работы | ||||
Таблица 2
| № варианта | Номер задачи контрольной работы | ||||
1. Введение в математический анализ
Найти пределы функций:
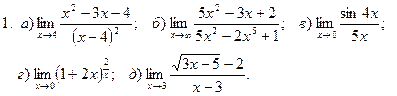
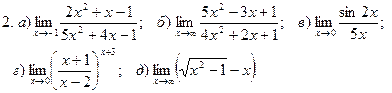
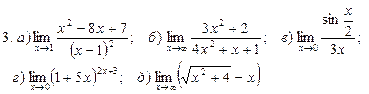
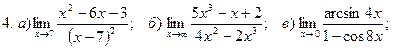
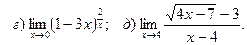
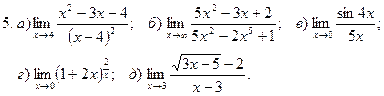
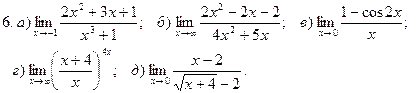
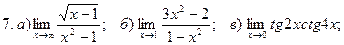
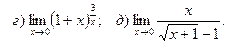
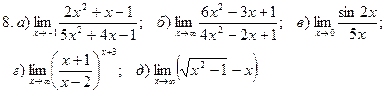
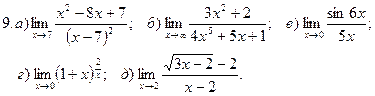
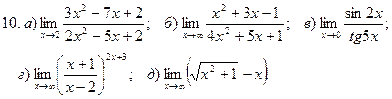 .
.
11. а) 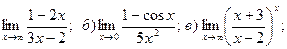
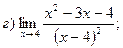
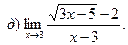
12. а) 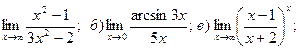
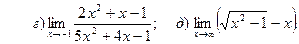
13. 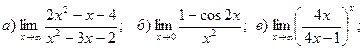
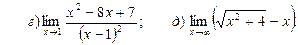
14. 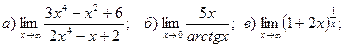
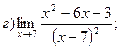
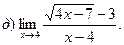
15. 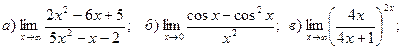
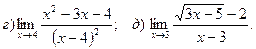
16. 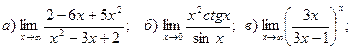
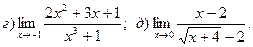
17. 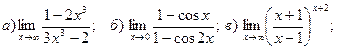
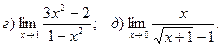
18. 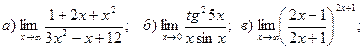
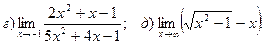
19. 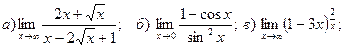
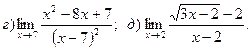
20. 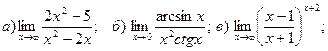
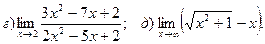
2. Дифференциальное исчисление функции одной переменной.
Найти производные данных функций.
21.а) 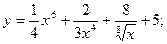 б)
б) 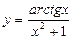 в) y =
в) y = 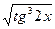 ;
;
г) y = 2 x - arcsin x; д) 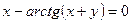 .
.
22.а) 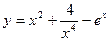 ; б) y =
; б) y = 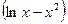
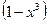 ; в) y =
; в) y = 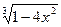 ;
;
г) y = e cos 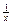 ; д)
; д) 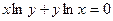 .
.
23.а) y = 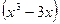 lnx; б) ) y =
lnx; б) ) y = 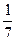 x7 +
x7 + 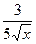 + 1;
+ 1;
в) y = ln 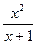 ; г) y = 2
; г) y = 2 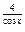 ; д)
; д) 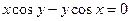 .
.
24.а) y = 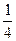 x8 +
x8 + 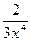 +
+ 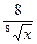 + 5; б) y =
+ 5; б) y = 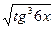 ; в) y =
; в) y = 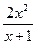 ; г) y = 3 x - arcsin x ; д)
; г) y = 3 x - arcsin x ; д) 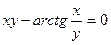
25.а) y = 2x3 - 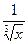 + ex; б) y =
+ ex; б) y = 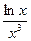 ; в) y =
; в) y = 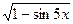 ;
;
г) y = 2 cos 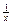 ; д)
; д) 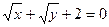 .
.
26.а) y = 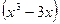 sinx; б) y =
sinx; б) y = 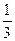 x3 +
x3 + 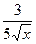 + 1; в) y = ln
+ 1; в) y = ln 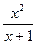 ;
;
г) y = 2 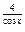 ; д)
; д) 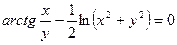 .
.
27.а) 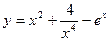 ; б) y =
; б) y = 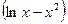
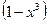 ; в)y =
; в)y = 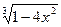 ; г) y =
; г) y = 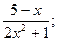 д)
д) 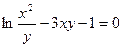 .
.
28.а) y = 3x4 – 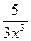 – 9
– 9 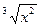 + 9; б)y =
+ 9; б)y = 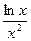 ; в) y = sin tg
; в) y = sin tg 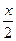 ;
;
г) y =( x2 - x) 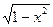 ; д)
; д) 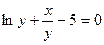 .
.
29.а) y = 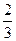 x3 –
x3 – 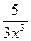 – 6
– 6 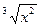 + 3; б)
+ 3; б) 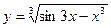 ; в) y = 5 sin3x; г)
; в) y = 5 sin3x; г) 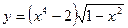 ; д)
; д) 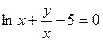 .
.
30.а) y = 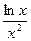 ; б) y = (3x – 4)6; в) y = 3x4 –
; б) y = (3x – 4)6; в) y = 3x4 – 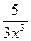 – 9
– 9 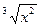 + 9; г) y =
+ 9; г) y = 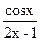 ; д)
; д) 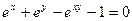 .
.
31.а) y = 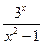 ; б)
; б) 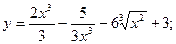 в) y = 5 sin3x + 2; г)
в) y = 5 sin3x + 2; г) 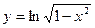 ; д)
; д) 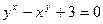 .
.
32.а) y = (x2 – 1)ex; б) y = 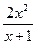 ; в) y =
; в) y = 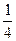 x8 +
x8 + 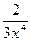 +
+ 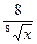 + 5; г)
+ 5; г) 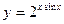 ; д)
; д) 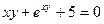 .
.
33.а) 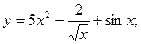 б)
б) 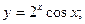 в)
в) 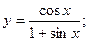 г)
г) 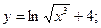 д)
д) 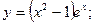 е)
е) 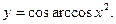
34.а) y = 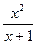 ; б) y = x2 + x sin x; в)
; б) y = x2 + x sin x; в) 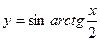 ;
;
г) y = 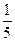 x5 –
x5 – 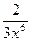 +
+ 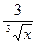 + 2; д)
+ 2; д) 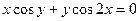 .
.
35.а) y = 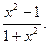 б)
б) 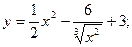 в)
в) 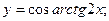 г)
г) 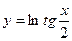 ; д) y = (e5x – 1)6; е)
; д) y = (e5x – 1)6; е) 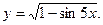
36.а) y = 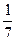 x7 +
x7 + 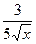 + 1; б) y =
+ 1; б) y = 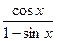 ; в)
; в) 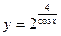 ;
;
г) 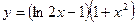 д)
д) 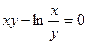 .
.
37.а) 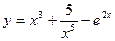 ; б) y =
; б) y = 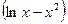
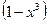 ; в)y =
; в)y = 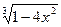 ;
;
г) y = 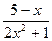 ; д)
; д) 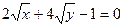 .
.
38.а) y = 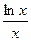 ; б) y = sin tg
; б) y = sin tg 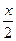 ; в) y =
; в) y = 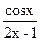 ;
;
г) y = 3x4 – 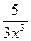 – 9
– 9 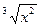 + 9; д)
+ 9; д) 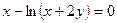 .
.
39.а) 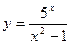 ; б)
; б) 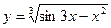 ; в) y = 5 sin3x;
; в) y = 5 sin3x;
г) 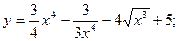 д)
д) 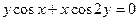
40.а) 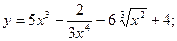 б) y =
б) y = 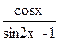 ; в) y = x
; в) y = x 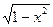 ; г) y = e sin3x + 2; д)
; г) y = e sin3x + 2; д) 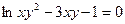 .
.
Исследовать функцию и построить ее график.
41. 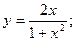 42.
42. 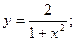 43.
43. 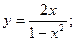 44.
44. 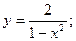
45. 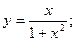 46.
46. 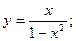 47.
47. 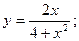 48.
48. 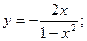
49. 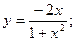 50.
50. 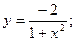 51.
51. 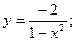 52.
52. 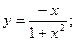
53. 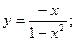 54.
54. 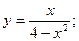 55.
55. 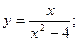 56.
56. 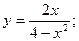
57. 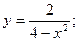 58.
58. 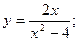 59.
59. 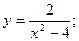 60.
60. 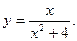
3. Дифференциальное исчисление функции нескольких переменных.
Найти экстремумы функции.
61. 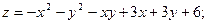
62. 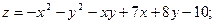
63. 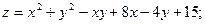
64. 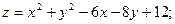
65. 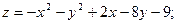
66. 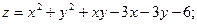
67. 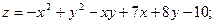
68. 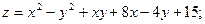
69. 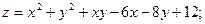
70. 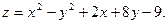
Найти наибольшее и наименьшее значение функции 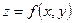 в данной замкнутой области.
в данной замкнутой области.
71. 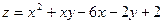 в прямоугольнике
в прямоугольнике

72. 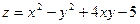 в треугольнике, ограниченном осями координат и прямой
в треугольнике, ограниченном осями координат и прямой 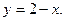
73. 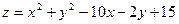 в прямоугольнике
в прямоугольнике

74. 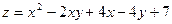 в области, ограниченной параболой
в области, ограниченной параболой 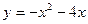 и осью абсцисс.
и осью абсцисс.
75. 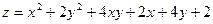 в квадрате
в квадрате

76. 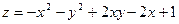 в треугольнике, ограниченном осями координат и прямой
в треугольнике, ограниченном осями координат и прямой 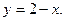
77. 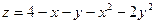 в треугольнике, ограниченном осями координат и прямой
в треугольнике, ограниченном осями координат и прямой 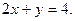
78. 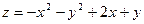 в треугольнике, ограниченном осями координат и прямой
в треугольнике, ограниченном осями координат и прямой 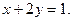
79. 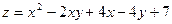 в области, ограниченной параболой
в области, ограниченной параболой 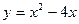 и осью абсцисс.
и осью абсцисс.
80. 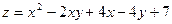 в области, ограниченной параболой
в области, ограниченной параболой 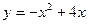 и осью абсцисс.
и осью абсцисс.
4. Интегральное исчисление.
№ 81.
1.Найти неопределенные интегралы.
а) 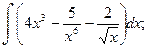 б)
б) 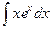 ; в)
; в) 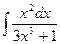 .
.
2.Вычислить определенные интегралы.
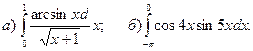
3.Найти несобственные интегралы, если они сходятся.
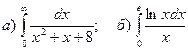 .
.
№ 82.
1.Найти неопределенные интегралы.
а) 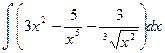 ; б)
; б) 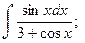 в)
в) 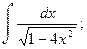 г)
г) 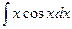 .
.
2.Вычислить определенные интегралы.
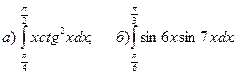
3.Найти несобственные интегралы, если они сходятся.
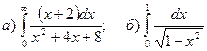 .
.
№ 83.
1.Найти неопределенные интегралы. 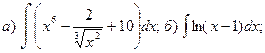
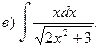
2.Вычислить определенные интегралы.
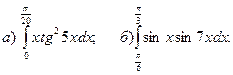
3.Найти несобственные интегралы, если они сходятся.
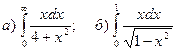 .
.
№ 84.
1.Найти неопределенные интегралы.
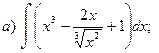
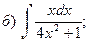 в)
в) 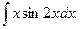
2.Вычислить определенные интегралы.
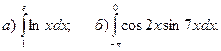
3.Найти несобственные интегралы, если они сходятся.
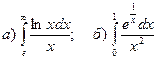 .
.
№ 85.
1.Найти неопределенные интегралы.
а) 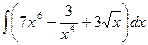 ; б)
; б) 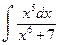 ; в)
; в) 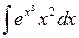 .
.
2.Вычислить определенные интегралы.
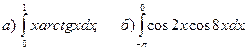 .
.
3.Найти несобственные интегралы, если они сходятся.
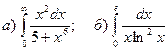 .
.
№ 86.
1.Найти неопределенные интегралы.
а) 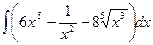 ; б)
; б) 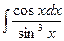 ; в)
; в) 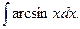
2.Вычислить определенные интегралы.
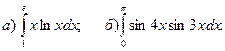
3.Найти несобственные интегралы, если они сходятся.
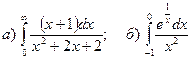 .
.
№ 87.
1.Найти неопределенные интегралы.
а) 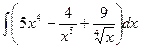 ; б)
; б) 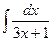 ; в)
; в) 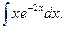
2.Вычислить определенные интегралы.
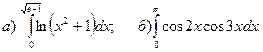
3.Найти несобственные интегралы, если они сходятся.
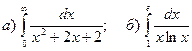 .
.
№ 88.
1.Найти неопределенные интегралы.
а) 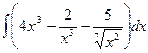 ; б)
; б) 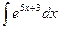 ; в)
; в) 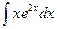 .
.
2.Вычислить определенные интегралы.
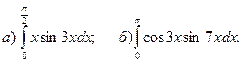
3.Найти несобственные интегралы, если они сходятся.
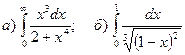 .
.
№ 89.
1.Найти неопределенные интегралы.
а) 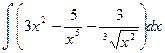 ; б)
; б) 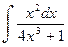 ; в)
; в) 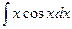 .
.
2.Вычислить определенные интегралы.
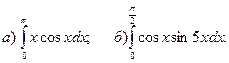
3.Найти несобственные интегралы, если они сходятся.
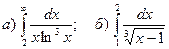 .
.
№ 90.
1.Найти неопределенные интегралы.
а) 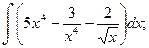 б)
б) 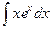 ; в)
; в) 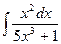 .
.
2.Вычислить определенные интегралы.
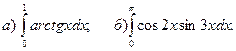
3.Найти несобственные интегралы или доказать, что они расходятся.
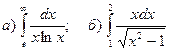 .
.
№91.
1.Найти неопределенные интегралы.
а) 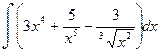 ; б)
; б) 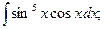 в)
в) 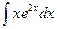 .
.
2.Вычислить определенные интегралы.
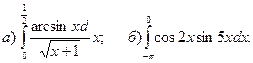
3.Найти несобственные интегралы, если они сходятся.
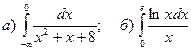 .
.
№ 92.
1.Найти неопределенные интегралы.
а) 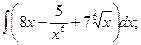 б)
б) 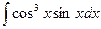 ; в)
; в) 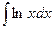 .
.
2.Вычислить определенные интегралы.
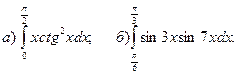
3.Найти несобственные интегралы, если они сходятся.
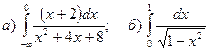 .
.
№ 93.
1. Найти неопределенные интегралы.
а) 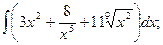 б)
б) 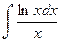 ; в)
; в) 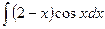 .
.
2. Вычислить определенные интегралы.
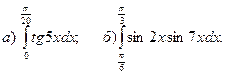
3.Найти несобственные интегралы, если они сходятся.
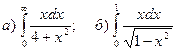 .
.
№ 94.
1.Найти неопределенные интегралы.
а) 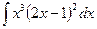 ; б)
; б) 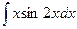 ; в)
; в) 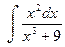 .
.
2.Вычислить определенные интегралы.
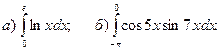
3.Найти несобственные интегралы, если они сходятся.
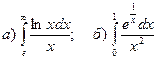 .
.
№ 95.
1.Найти неопределенные интегралы.
а) 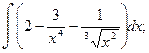 б)
б) 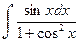 ; в)
; в) 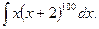
2.Вычислить определенные интегралы.
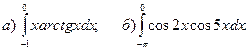 .
.
3.Найти несобственные интегралы, если они сходятся.
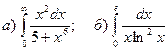 .
.
№ 96.
1.Найти неопределенные интегралы.
а) 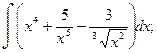 б)
б) 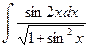 ; в)
; в) 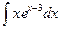 .
.
2.Вычислить определенные интегралы.
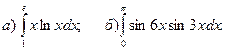
3.Найти несобственные интегралы, если они сходятся.
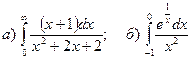 .
.
№ 97.
1.Найти неопределенные интегралы.
а) 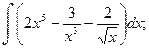 б)
б) 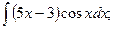 в)
в) 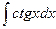 .
.
2.Вычислить определенные интегралы.
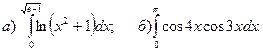
3.Найти несобственные интегралы, если они сходятся.
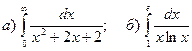 .
.
№ 98.
1.Найти неопределенные интегралы.
а) 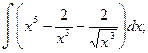 б)
б) 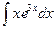 ; в)
; в) 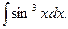
2.Вычислить определенные интегралы.
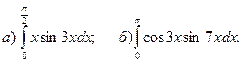
3.Найти несобственные интегралы, если они сходятся.
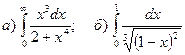 .
.
№ 99.
1.Найти неопределенные интегралы.
а) 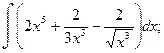 б)
б) 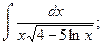 в)
в) 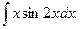 .
.
2.Вычислить определенные интегралы.
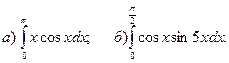
3.Найти несобственные интегралы, если они сходятся.
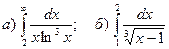 .
.
№ 100.
1.Найти неопределенные интегралы.
а) 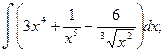 б)
б) 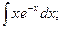 в)
в) 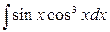 .
.
2.Вычислить определенные интегралы.
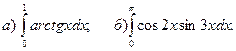
3.Найти несобственные интегралы или доказать, что они расходятся.
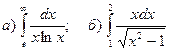 .
.
Пример 4.
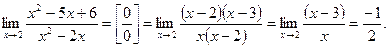
Пример 5. 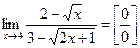 =
=
Правило 5. Если подпредельное выражение содержит тригонометрические функции, тогда, чтобы раскрыть неопределенность вида  используют первый замечательный предел.
используют первый замечательный предел.
Пример 6.
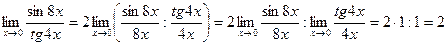 Пример 7.
Пример 7.
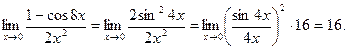
Правило 6. Чтобы раскрыть неопределенность вида 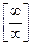 при
при 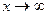 , числитель и знаменатель подпредельной дроби необходимо разделить на высшую степень аргумента и находить далее предел частного.
, числитель и знаменатель подпредельной дроби необходимо разделить на высшую степень аргумента и находить далее предел частного.
Возможны результаты:
1) искомый предел равен отношению коэффициентов при старших степенях аргумента числителя и знаменателя, если эти степени одинаковы;
2) предел равен бесконечности, если степень аргумента числителя выше степени аргумента знаменателя;
3) предел равен нулю, если степень аргумента числителя ниже степени аргумента знаменателя.
Пример 8. 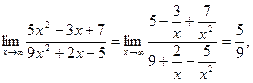
т.к. 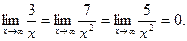
Пример 9. 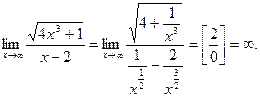
Пример 10.
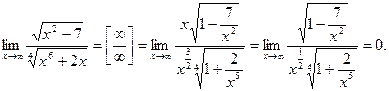
Можно было сразу сравнить степени аргумента числителя и знаменателя.
Пример 8. Степени равны, значит, предел равен отношению коэффициентов при старших степенях, т.е. 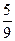 .
.
Пример 9. Степень числителя 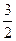 , знаменателя – 1, значит, предел равен
, знаменателя – 1, значит, предел равен 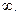
Пример 10. Степень числителя 1, знаменателя – 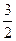 , значит, предел равен 0.
, значит, предел равен 0.
Правило 7. Чтобы раскрыть неопределенность вида 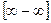 , числитель и знаменатель подпредельной дроби необходимо домножить на сопряженное выражение.
, числитель и знаменатель подпредельной дроби необходимо домножить на сопряженное выражение.
Пример 11.
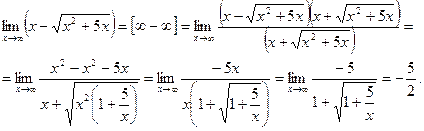
Правило 8. Чтобы раскрыть неопределенность вида 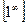 используют второй замечательный предел и его следствия.
используют второй замечательный предел и его следствия.
Можно доказать, что 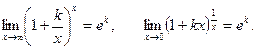
Пример 12.
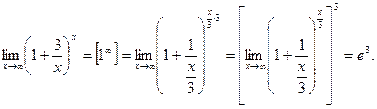
Пример 13. 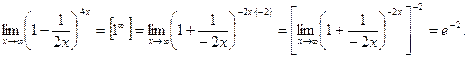 Пример 14.
Пример 14.
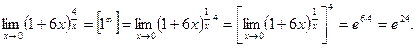
Правило 9. При раскрытии неопределенностей, подпредельная функция которых содержит б.м.в., необходимо заменить пределы этих б.м. на пределы б.м., эквивалентных им.
Пример 15.
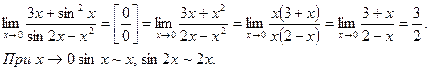
Пример 16. 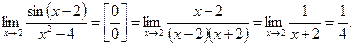
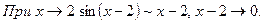
Правило 10. Правило Лопиталя (см. главу 2, с. 39).
Пример 19.
а) 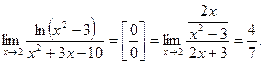
б) 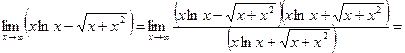
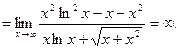
Неопределенный интеграл
Определение 1. Функция 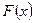 называется первообразной для
называется первообразной для 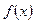 , если
, если 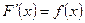 .
.
Определение 2. Неопределенным интегралом от функции f(x) называется совокупность всех первообразных для этой функции.
Обозначение: 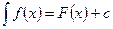 , где c - произвольная постоянная.
, где c - произвольная постоянная.
Свойства неопределенного интеграла
1. Производная неопределенного интеграла: 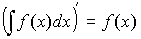
2. Дифференциал неопределенного интеграла: 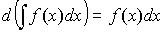 .
.
3. Неопределенный интеграл от дифференциала: 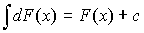 .
.
4. Неопределенный интеграл от суммы (разности) двух функций:
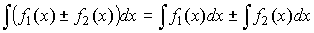 ;
;
5. Вынесение постоянного множителя за знак неопределенного интеграла:
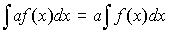
Таблица неопределенных интегралов
1) 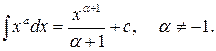
2) 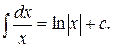
3) 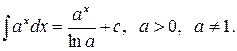
Если 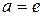 , то
, то 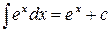 .
.
4) 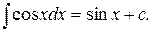
5) 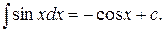
6) 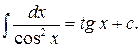
7) 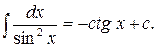
8) 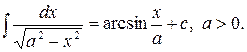
9) 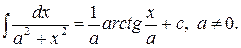
10) 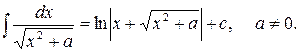
11) 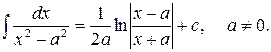
Все формулы справедливы также в случае, если переменную 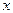 заменить на некоторую другую функцию. Так, если в формуле 2 заменить
заменить на некоторую другую функцию. Так, если в формуле 2 заменить 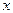 на
на 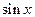 , то получим, что
, то получим, что
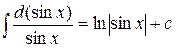 .
.
Основные методы интегрирования
1. Использование свойств неопределенного интеграла.
Пример 25.
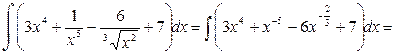
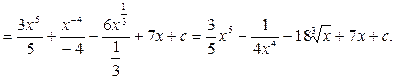
2. Подведение под знак дифференциала.
Пример 26. 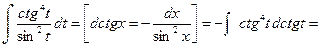
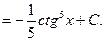
3. Метод замены переменной:
а) замена 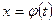 в интеграле
в интеграле 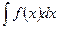 :
: 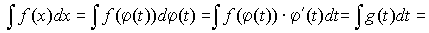
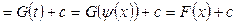 , где
, где
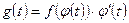 - функция, интегрируемая легче, чем исходная;
- функция, интегрируемая легче, чем исходная;
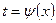 - функция, обратная функции
- функция, обратная функции 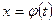 ;
;
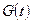 - первообразная функции
- первообразная функции 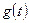 .
.
Пример 27. 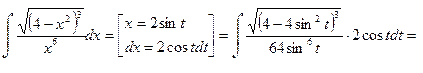
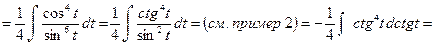
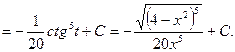
б) замена 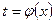 в интеграле вида:
в интеграле вида:
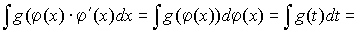
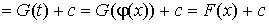 ;
;
Пример 28. 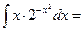
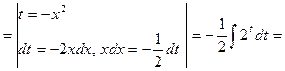
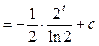
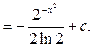
Пример 29. 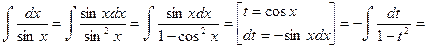
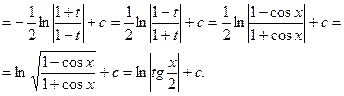
4. Метод интегрирования по частям:
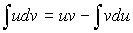
Пример 30.
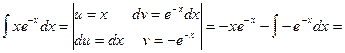
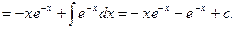
Пример 31.
