Практические применения уравнения Бернулли

На практике уравнение Бернулли используется для определения скоростей (рис. 2.11) и расходов жидкостей и газов, напора насоса, времени истечения жидкостей из резервуаров. На рис. 2.12 приведена схема измерение расхода с помощью диафрагмы, на рис. 2.13 и 2.14- с помощью сопла и трубы Вентури.

Рис. 2.11. Измерение скорости жидкости пневмометрической трубкой

Рис. 2.12. Мерная диафрагма

Рис. 2.13.Мерное сопло

Рис. 2.14. Труба Вентури

Зависимость для определения объемного расхода жидкости через дроссельные устройства (диафрагму, мерное сопло, трубу Вентури) имеет вид:

(2.66)

,

где – коэффициент расхода дроссельного прибора. Значения коэффициента определяются опытным путем и приводятся в специальной литературе; – диаметр трубопровода; –диаметр наиболее узкого сечения мерного устройства.

Объемный расход жидкости при истечении через круглое отверстие в днище сосуда с постоянным уровнем жидкости:

(2.67)

Из уравнения следует, что расход жидкости, вытекающей через отверстие в тонком днище, зависит от высоты постоянного уровня жидкости над отверстием и от размера отверстия, но не зависит от формы сосуда (рис. 2.15).

С помощью уравнения Бернулли можно также определять время опорожнения сосуда от жидкости, имеющего постоянное поперечное сечение, от высоты до :

(2.68)

а также решать другие прикладные задачи, например, вычислять напор насоса.

Рис. 2.15. Истечение жидкости из сосуда:

а – при постоянном уровне; б – при переменном уровне

Гидродинамическое подобие

Выше отмечалось, что дифференциальные уравнения Навье–Стокса невозможно решить для большинства технических задач.

Теория подобия позволяет преобразовать уравнения Навье–Стокса и получить из них некоторую общую функциональную зависимость между критериями подобия, характеризующими силы, действующие в потоке при движении вязкой жидкости.

Перепишем уравнение Навье–Стокса для капельной жидкости в развернутом виде для вертикальной оси :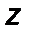

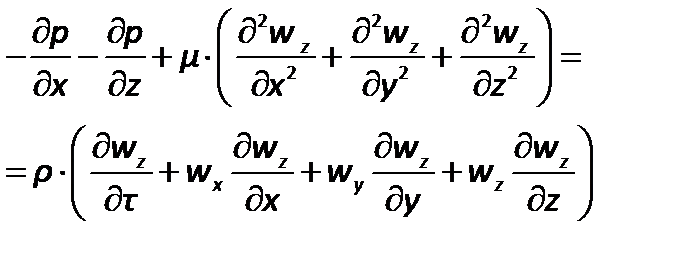(2.69)

Для получения безразмерных комплексов, критериев подобия, необходимо одну часть уравнения разделить на другую. Поскольку каждое из слагаемых уравнения выражает силу, действующую в потоке, то, приняв одну из них за единицу измерения – масштаб сил, безразмерные комплексы будут представлять собой соотношения сил к принятому масштабу. За масштаб сил в движущемся потоке принимается сила инерции.

Если движение жидкости установившееся, то ее скорость не зависит от времени. Член, характеризующий силу инерции после замены дифференциалов конечными величинами (операция отбрасывания знаков математических операторов), будет иметь вид

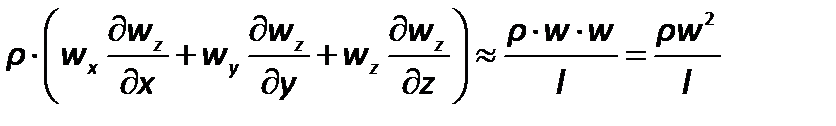(2.70)

где 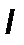– определяющий линейный размер.

Член, отражающий влияние сил тяжести на течение жидкости, рав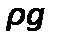ен .Член 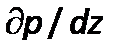, характеризующий влияние сил давления, представляется ввиде

.

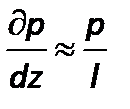Слагаемое, отражающее действие сил трения, представляется как

.

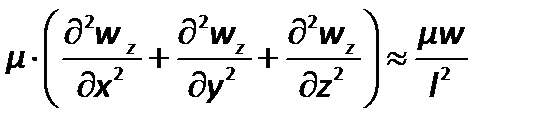Разделим члены одной части уравнения на члены другой его части и установим, таким образом, выражения, характеризующие соотношения между соответствующими силами и силой инерции.

Выражение, характеризующее отношение силы инерции и силы тяжести, называется критерием Фруда:

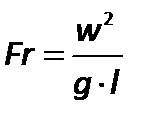(2.71)

Критерий Фруда отражает влияние сил тяжести, или собственного веса, на движение жидкости. Представляет собой меру отношения силы инерции к силе тяжести в подобных потоках.

Соотношение между силами давления и инерции представляет собой критерий Эйлера:

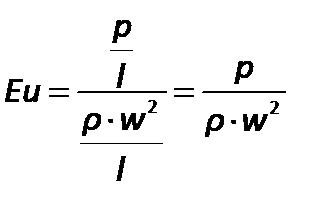(2.72)

Обычно критерию Эйлера придают иной вид, введя в него вместо абсолютного давления разность давлений 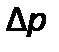между двумя какими-либо точками жидкости:

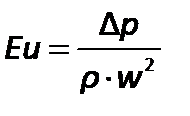(2.73)

Критерий Эйлера отражает влияние перепада гидростатического давления на движение жидкости. Его величина характеризует отношение изменения силы гидростатического давления к силе инерции в подобных потоках.

Безразмерный комплекс, являющийся отношением инерционных сил к силам трения в подобных потоках, представляет известный намкритерий Рейнольдса:

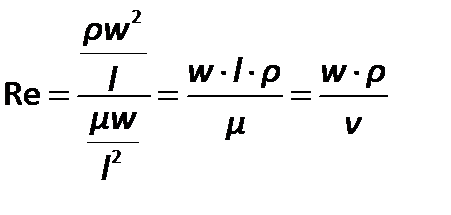(2.74)

Величина 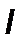в критерии Рейнольдса, как и в других критериях подобия, представляет определяющий линейный размер. При движении жидкости через трубопроводы или аппараты за этот размер принимается диаметр, а в случае некруглого сечения потока – эквивалентный диаметр .

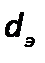При неустановившемся течении жидкости в уравнении Навье–Стокса 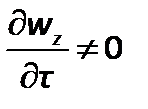. Преобразуем слагаемое, отражающее влияние нестационарности течения, 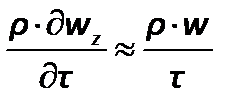. Безразмерный комплекс, полученный отношением силы инерции к члену уравнения, отражающему нестационарный процесс,называется критерием гомохронности:

(2.75)

Критерий гомохронности учитывает неустановившийся характер движенияжидкости в подобных потоках.

Во всех сходственных точках подобно движущихся потоков жидкости критерии подобия равны (одни и те же – ), т.е. , , , .

Согласно второй теореме подобия, решение уравнений Навье - Стокса можно представить в виде функциональной зависимости между полученными критериями подобия, т.е.:

(2.76)

или после добавления симплексов геометрического подобия, представляющих собой отношение одноименных геометрических размеров, характеризующих реальный объект и модель, к определяющим получим

(2.77)

где - симплексы геометрического подобия.

Все критерии в критериальном уравнении самого общего вида, кроме критерия Эйлера, являются определяющими, т.к. они составлены исключительно из величин, входящих в условия однозначности.В критерий Эйлера входит разность давлений , величина которой при движении жидкости по трубе определяется формой трубы ( ), физическими свойствами жидкости ( ) и распределением скоростей у входа в трубу и у ее стенок (начальные и граничные условия). Поэтому, согласно третьей теореме подобия, для подобия двух систем необходимо и достаточно соблюдения равенства значений и симплексов геометрического подобия. Следствием выполнения этих условий будет равенство значений определяемого критерия в сходственных точках подобных потоков. Поэтому критериальное уравнение общего видапредставляют в виде зависимости определяемого критерия от определяющих критериев:

(2.78)

Зависимости подобного вида называют обобщенными или критериальными уравнениями гидродинамики.

Как уже было сказано выше, подобные функции наиболее удобно апроксимировать степенными зависимостями вида

(2.79)

или после подстановки соответствующих комплексов величин

(2.80)

Если движение жидкости является стационарным, то критерий может быть исключен из уравнения. Поэтому для установившегося течения жидкости обобщенное уравнение гидродинамики будет иметь вид

(2.81)