Основное уравнение гидростатики

Из уравнений (2.15) следует, что p=f(z), т.к. 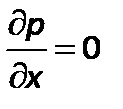и , и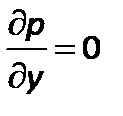наче жидкость должна была бы двигаться по горизонтали.

В этом случае частная производная 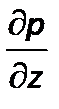изменяется наполную производную 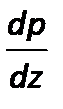, тогда:

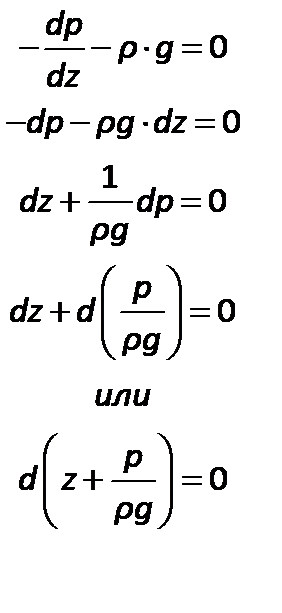(2.16)

После интегрирования

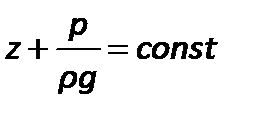(2.17)

для двух произвольных горизонтальных плоскостей 1 и 2 основное уравнение гидростатики имеет вид:

.

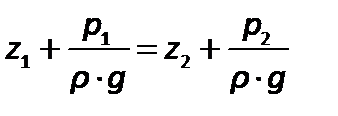Это уравнение можно записать как:

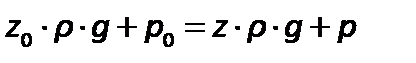
или

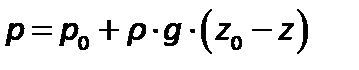(2.18)

Уравнение (2.17) является выражением закона Паскаля, согласно которому давление, создаваемое в любой точке покоящейся несжимаемой жидкости, передается одинаково всем точкам ее объема.

При изменении p₀ в точке z₀ на какую-либо величину давление pво всякой другой точке изменяется на эту же величину (рис. 2.3).

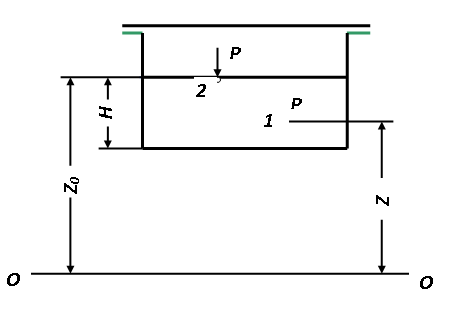
Рис. 2.3. К основному уравнению гидростатики

2.2.2 Практическое приложение уравнения гидростатики

Принцип сообщающихся сосудов

Пусть два открытых сообщающихся сосуда заполнены жидкостью плотностью (рис. 2.4).

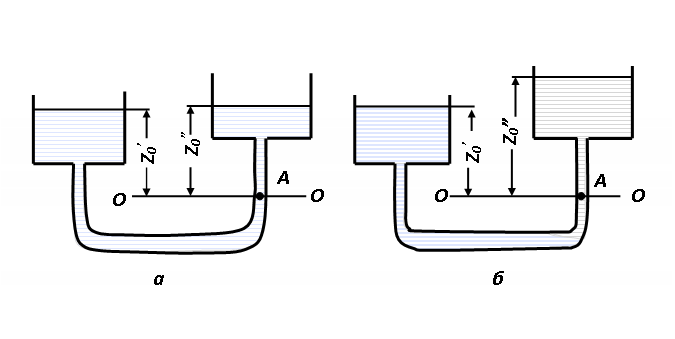
Рис. 2.4. Условия равновесия в сообщающихся сосудах:

а – однородная жидкость; б –разнородные (несмешивающиеся) жидкости

Рассмотрим произвольную плоскость сравнения0 -0и некоторую точку А внутри жидкости, лежащую в этой плоскости. Если считать точку Апринадлежащей левому сосуду, то, согласно уравнению (2.17), давление в этой точке равно:

.

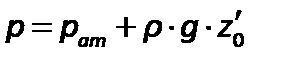Если считать точку А принадлежащей правому сосуду, то давление в ней равно:

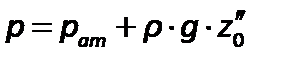
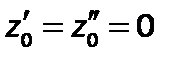( , т.к. плоскость 0 -0проходит черезточку А).

При равновесии для каждой точки давление одинаково в любом направлении, иначе бы происходило перемещение жидкости. Следовательно

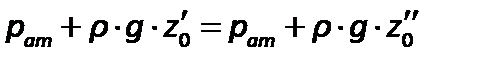
или

.

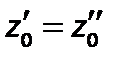Аналогичный вывод можно сделать, если рассмотреть сообщающиеся сосуды, в которых давление над свободной поверхностью жидкости одинаково.

Таким образом, в открытых или закрытых сообщающихся сосудах, находящихся под одинаковым давлением и заполненных однородной жидкостью, уровни последней располагаются на одной высоте независимо от формы и поперечного сечения сосудов.

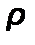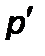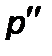Если сосуды заполнены одной жидкостью плотностью , но давления над уровнем жидкости в них неодинаковы и равны и , то

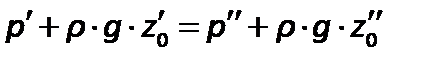
откуда

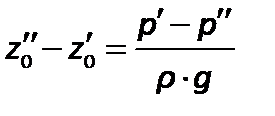(2.19)

Уравнение (2.18) применяется при измерении давлений или разностей давлений с помощью дифференциальных -образных манометров.

Пневматическое измерение количества жидкости в подземных резервуарах

Для контроля за количеством жидкости в подземном резервуареустанавливают трубу, нижний конец которой доходит почти до днища. Давление над жидкостью в резервуаре равно .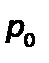

По трубе подают сжатый воздух или другой газ, постепенно повышая его давление, измеряемое манометром. Когда воздух преодолеет сопротивление столба жидкости в резервуаре и начнет барботировать через слой жидкости, давление, измеряемое манометром, перестанет возрастать и станет равным:

.

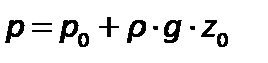Отсюда уровень жидкости в резервуаре равен:

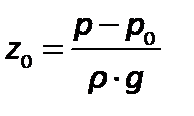(2.20)

По величине и известной площади поперечного сечения резервуара определяют объем находящейся в нем жидкости.

Гидростатические машины

На использовании основного уравнения гидростатики основана работа гидравлических прессов, домкратов, гидроцилиндров и др. Если в гидропрессе
(рис. 2.5) приложить небольшое усилие к поршню 1, перемещаемому в цилиндре меньшего диаметра 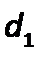, и создать давление на поршень, то, согласно закону Паскаля, такое же давление будет приходиться на поршень 2 в цилиндре с большим диаметром 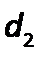, при этом сила давления на поршень 1 составит

,

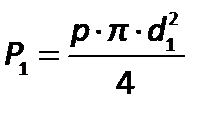а сила давления на поршень 2

.

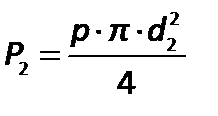В результате поршень в цилиндре большего диаметра передает силу давления во столько раз большую, чем сила, приложенная к поршню в цилиндре меньшего диаметра, насколько поперечное сечение цилиндра 2 больше, чем цилиндра 1, т.е.:

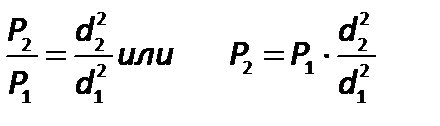(2.21)

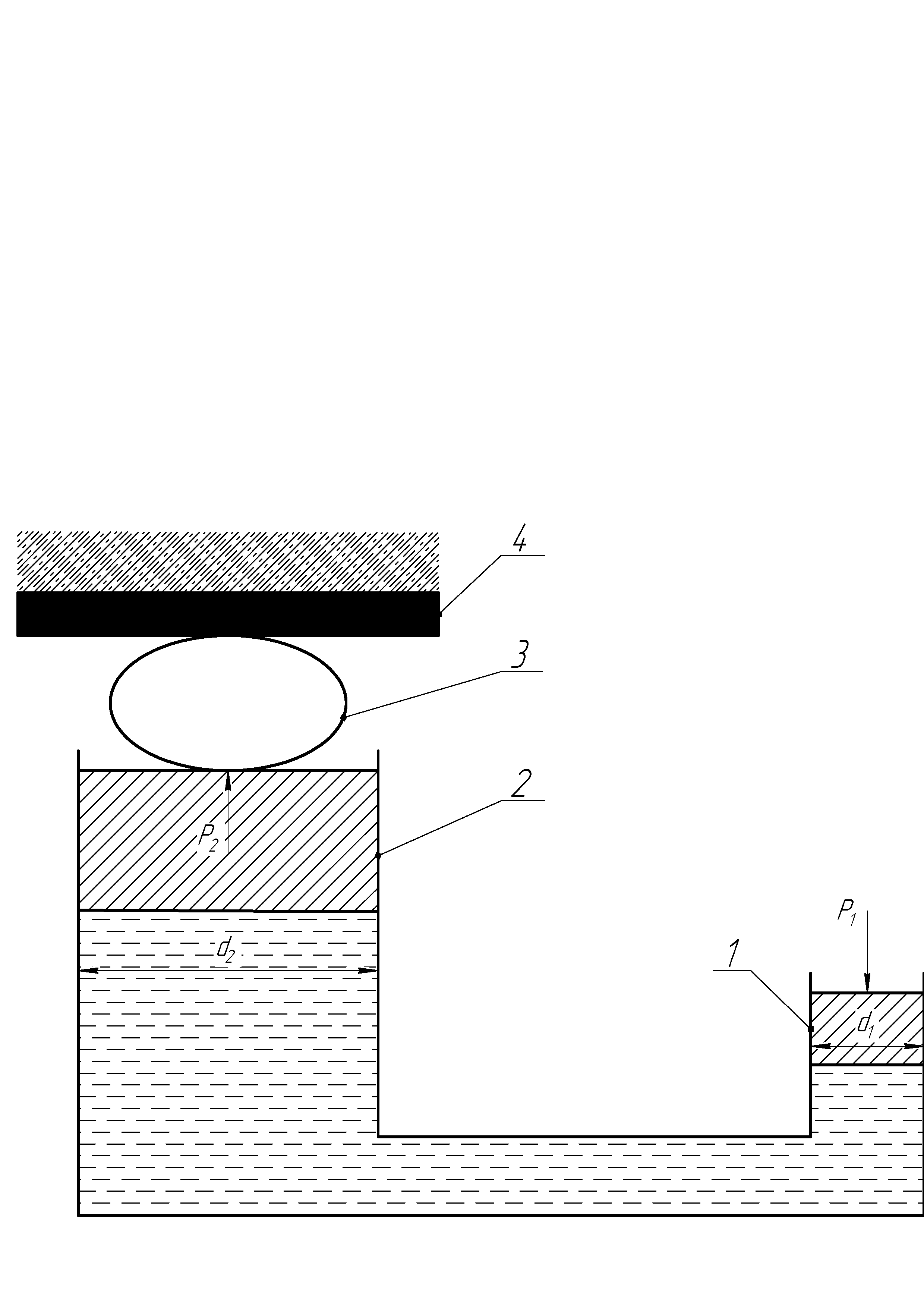
Рис. 2.5. Схема гидравлического пресса:
1, 2 – цилиндры пресса;3 – изделие; 4 – неподвижная плита