Численное решение уравнений и систем уравнений

Численное решение уравнений и систем уравнений

Система Mathcad обладает средствами как численного, так и аналитического решения уравнений и систем уравнений. Рассмотрим сначала способы численного решения.

Любое уравнение может быть представлено в виде равенства некоторой функции нулю, например, f(x) = 0. Такая форма записи наиболее удобна для нахождения корней уравнения, в том числе и в Mathcad. Поэтому в дальнейшем обозначим f(x) − левая часть уравнения, когда правая часть равна нулю.

В ходе численного решения обычно выделяют два этапа:

· отделение корней − определение интервала нахождения каждого корня, или даже определение приблизительного значения корня;

· уточнение корней − нахождение значения корня с указанной точностью.

Различают следующие способы отделения корней:

· аналитический;

· графический;

· по смыслу задачи;

· исходя из решения аналогичных задач и др.

Аналитический способ отделения корней уравнения заключается в следующем:

1) находится производная левой части уравнения f’(x) и вычисляются корни производной;

2) составляются таблицы значений переменной х и функции f(x) при значениях х, равных критическим точкам функции (корням производной) и граничным значениям (исходя из области допустимых значений неизвестного), с целью определения перемены знака функции f(x);

3) промежутки, на которых имеются корни уравнения f(x) = 0 (функция f(x) меняет знак), уменьшаются до длины, меньшей 1, для чего составляются новые таблицы значений х и f(x).

Нахождение критических точек функции f(x) можно опустить, сразу составив таблицы значений аргумента и функции.

Учитывая возможности пакета Mathcad, наиболее наглядным будет отделение корней уравнения графическим способом, который будет рассмотрен ниже на примерах.

Использование функции root

Встроенная функция root пакета Mathcad предназначена для нахождения нулей функций или для решения одного уравнения с одной неизвестной.

Функция записывается в виде

root(f(x1, x2, ...), xi, [a, b]),

и возвращает значение переменной xi, при котором функция f(x1,x2, ...) обращается в ноль. Аргументы функции root:

· f(x1, x2, ...) – скалярная функция произвольного числа переменных;

· xi – переменная, относительно которой требуется решить уравнение;

· a, b (необязательные) – действительные числа, такие что a < b, задающие интервал поиска корня.

Если заданы a и b, корень ищется на промежутке [a, b]. В противном случае переменная xi должна быть определена перед вызовом функции root некоторым начальным приближением. Для уточнения комплексного корня желательно задавать комплексное начальное приближение, так как значение функции root зависит от выбора начального приближения.

Точность нахождения корня с помощью функции root зависит от значения системной переменной TOL (Convergence Tolerance − Допуск сходимости), которое по умолчанию равно 10^-3. Чем меньше значение TOL, тем точнее, вообще говоря, находится корень уравнения. Однако оптимальным является TOL = 10^-5. Более того, при выборе TOL < 10^-12 улучшение результата происходить не будет, а используемые алгоритмы могут не сходиться. Переопределить значение TOL можно:

· присваиванием, например: ;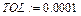

· вызовом из главного меню окна математических свойств документа Math Options и указанием необходимого значения на вкладке Build-In Variables (Встроенные переменные).

Случается, что функция root не может найти корни уравнения, если:

· уравнение не имеет корней или на заданном с помощью функции root интервале [a, b] находится более одного корня;

· корни расположены далеко от начального приближения;

· между начальным приближением и корнем находится точка локального максимума или минимума функции;

· уравнение имеет комплексные корни, а задано − действительное начальное приближение;

· между начальным приближением и корнем функция терпит разрыв;

· корни расположены близко друг от друга;

· в окрестности корня − плоские участки или малый наклон функции.

Зачастую задание более точного начального приближения, изменение границ интервала [a, b] нахождения корня или изменение значения переменной TOL позволяет устранить ошибку применения функции root.

Использование матричной функции rref(A)

Реализовать широко известный метод решения систем линейных алгебраических уравнений путем последовательного исключения неизвестных (метод Гаусса) позволяет встроенная функция rref(M), возвращающая ступенчатый вид матрицы M. Если в качестве аргумента взять расширенную матрицу AR системы, то функции rref(AR) возвратит матрицу, на диагонали которой – единицы, а последний столбец представляет собой столбец решений системы.

Численное решение уравнений и систем уравнений

Система Mathcad обладает средствами как численного, так и аналитического решения уравнений и систем уравнений. Рассмотрим сначала способы численного решения.

Любое уравнение может быть представлено в виде равенства некоторой функции нулю, например, f(x) = 0. Такая форма записи наиболее удобна для нахождения корней уравнения, в том числе и в Mathcad. Поэтому в дальнейшем обозначим f(x) − левая часть уравнения, когда правая часть равна нулю.

В ходе численного решения обычно выделяют два этапа:

· отделение корней − определение интервала нахождения каждого корня, или даже определение приблизительного значения корня;

· уточнение корней − нахождение значения корня с указанной точностью.

Различают следующие способы отделения корней:

· аналитический;

· графический;

· по смыслу задачи;

· исходя из решения аналогичных задач и др.

Аналитический способ отделения корней уравнения заключается в следующем:

1) находится производная левой части уравнения f’(x) и вычисляются корни производной;

2) составляются таблицы значений переменной х и функции f(x) при значениях х, равных критическим точкам функции (корням производной) и граничным значениям (исходя из области допустимых значений неизвестного), с целью определения перемены знака функции f(x);

3) промежутки, на которых имеются корни уравнения f(x) = 0 (функция f(x) меняет знак), уменьшаются до длины, меньшей 1, для чего составляются новые таблицы значений х и f(x).

Нахождение критических точек функции f(x) можно опустить, сразу составив таблицы значений аргумента и функции.

Учитывая возможности пакета Mathcad, наиболее наглядным будет отделение корней уравнения графическим способом, который будет рассмотрен ниже на примерах.

Использование функции root

Встроенная функция root пакета Mathcad предназначена для нахождения нулей функций или для решения одного уравнения с одной неизвестной.

Функция записывается в виде

root(f(x1, x2, ...), xi, [a, b]),

и возвращает значение переменной xi, при котором функция f(x1,x2, ...) обращается в ноль. Аргументы функции root:

· f(x1, x2, ...) – скалярная функция произвольного числа переменных;

· xi – переменная, относительно которой требуется решить уравнение;

· a, b (необязательные) – действительные числа, такие что a < b, задающие интервал поиска корня.

Если заданы a и b, корень ищется на промежутке [a, b]. В противном случае переменная xi должна быть определена перед вызовом функции root некоторым начальным приближением. Для уточнения комплексного корня желательно задавать комплексное начальное приближение, так как значение функции root зависит от выбора начального приближения.

Точность нахождения корня с помощью функции root зависит от значения системной переменной TOL (Convergence Tolerance − Допуск сходимости), которое по умолчанию равно 10^-3. Чем меньше значение TOL, тем точнее, вообще говоря, находится корень уравнения. Однако оптимальным является TOL = 10^-5. Более того, при выборе TOL < 10^-12 улучшение результата происходить не будет, а используемые алгоритмы могут не сходиться. Переопределить значение TOL можно:

· присваиванием, например: ;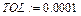

· вызовом из главного меню окна математических свойств документа Math Options и указанием необходимого значения на вкладке Build-In Variables (Встроенные переменные).

Случается, что функция root не может найти корни уравнения, если:

· уравнение не имеет корней или на заданном с помощью функции root интервале [a, b] находится более одного корня;

· корни расположены далеко от начального приближения;

· между начальным приближением и корнем находится точка локального максимума или минимума функции;

· уравнение имеет комплексные корни, а задано − действительное начальное приближение;

· между начальным приближением и корнем функция терпит разрыв;

· корни расположены близко друг от друга;

· в окрестности корня − плоские участки или малый наклон функции.

Зачастую задание более точного начального приближения, изменение границ интервала [a, b] нахождения корня или изменение значения переменной TOL позволяет устранить ошибку применения функции root.