Решение нелинейных уравнений и их систем

Хотя в ядро MATLAB последних версий встроено около 900 операторов и функций, пользователю всегда может потребоваться та или иная функция, отсутствующая в ядре. Язык программирования системы MATLAB предоставляет ряд возможностей для задания функции пользователя. Одна из таких возможностей – задание своих функций в виде m– файлов, для создания которых может использоваться как встроенный редактор Editor/ Debugger (открывается командой New из меню File), так и любой текстовый редактор, поддерживающий формат ASCII. Подготовленный и записанный на диск m-файл становится частью системы, и его можно вызывать как из командной строки, так и из другого m-файла.

Редактор/отладчик выполняет синтаксический контроль программного кода по мере ввода текста. При этом используются следующие цветовые выделения:

· ключевые слова языка программирования — синий цвет;

· операторы, константы и переменные — черный цвет;

· комментарии после знака % — зеленый цвет;

· символьные переменные (в апострофах) — зеленый цвет;

· синтаксические ошибки — красный цвет.

Помимо синтаксического контроля редактор/отладчик позволяет устанавливать в тексте файла специальные метки, именуемые точками прерывания (breakpoints). При их достижении вычисления приостанавливаются, и пользователь может оценить промежуточные результаты вычислений, проверить правильность выполнения циклов и т. д. Для удобства работы с редактором/отладчиком строки программы в нем нумеруются в последовательном порядке.

М-файлы, создаваемые редактором/отладчиком, делятся на два класса: файлы-сценарии или Script-файлы, не имеющие входных параметров, и файлы-функции, имеющие входные параметры. Script-файл использует глобальные переменные, значения которых могут быть изменены в любой момент сеанса работы и в любом месте программы. Для запуска файла-сценария из командной строки MATLAB достаточно просто указать его имя в этой строке. Файл-функция отличается от файла-сценария прежде всего тем, что созданная им функция имеет входные и выходные параметры.

Строка заголовка функции начинается с объявления function, после которого указывается имя выходного параметра, заключенное в квадратные скобки. Затем следует знак равенства, имя самой функции и заключенный в круглые скобки список ее входных параметров. После заголовка идет тело функции, в котором задаются инструкции необходимые для вычисления значений выходного аргумента на основе входных данных. Например,

function [f] = fun(x)

f = 0.25 * x +cos(x)-1;

Вызов рассмотренной в примере функции может иметь следующие виды:

>>fun(0)

>>x = fun(pi)

Еще одна возможность для создания функции пользователя заключается в применении объектов класса дескрипторов функций, задаваемых с помощью символа @, например: f=@exp. Численные значения функций, заданных дескрипторами, вычисляются с помощью функции feval(), например, feval(f,1,0).

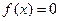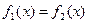Довольно часто возникает задача решения нелинейного уравнения вида или . Последнее, однако, можно свести к виду 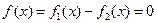. Таким образом, данная задача сводится к нахождению значений аргумента х функции f(x) одной переменной, при котором значение функции равно нулю. В системе MATLAB имеется ряд функций для решения данной задачи, например, функция fzero(). В зависимости от формы задания функции fzero() реализуются следующие хорошо известные численные методы поиска нуля функции: деления отрезка пополам, секущей и обратной квадратичной интерполяции. Приведем некоторые из них:

fzero( @fun, x0, options) — возвращает уточненное значение начального приближения х0, при котором достигается нуль функции fun, используя параметры вычислений из вектора options (не является обязательным параметром): tolX – конечное допустимое отклонение по значению х, maxfunevals – максимально число допустимых расчетов функции, maxiter – максимальное число допустимых итераций, display – уровень отображения ('off' отображение не производится, 'iter' отображение проводится на каждой итерации, 'final' (принимается по умолчанию) отображение только конечной информации). Перечисленные параметры следует предварительно установить при помощи команды optimset(). Например, options=optimset('Display','iter'). Возвращенное значение близко к точке, где функция меняет знак, или равно NaN, если такая точка не найдена;

fzero(@fun,[xl x2], options) — возвращает значение х, при котором fun(x)=0, с заданием интервала поиска с помощью вектора x=[xl х2], такого, что знак fun(xl) отличается от знака fun(x2). Если это не так, выдается сообщение об ошибке. Вызов функции fzero с интервалом гарантирует, что fzero возвратит значение, близкое к точке, где fun изменяет знак.

Приведенный ниже пример показывает приближенное вычисление корня уравнения cos(x)=0 с представлением косинуса дескриптором:

» х= fzero(@cos, [1 3])

В более сложных случаях рекомендуется строить график функции f(x) для приближенного определения корней и интервалов, в пределах которых они находятся.

Рассмотрим еще один пример решения нелинейного уравнения 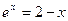. На первом этапе решения создадим m-файл fun.m, листинг которого представлен ниже:

function [ f]=fun(x)

f=exp(x)-2+x;

Далее построим график функции fun, используя следующую последовательность команд:

>>х=-5:0.1:5;

>>plot(x,funl(x));grid on;

Результат построения представлен на рис. 5.7 .

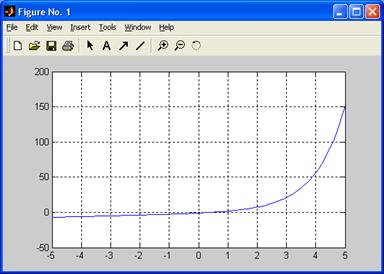
Рис. 5.7. График функции f=exp(x)-2+x.

Из рисунка нетрудно заметить, что значения корня заключено в интервале [-1, 1]. Найдем его, используя функцию fzero(), предварительно задав точность нахождения корня:

>> options=optimset('Display','final', 'tolX', 10^(-6));

>>x=fzero( @fun, [-1 1], options)

В результате получим корень уравнения х = 0.4429.

Для решения систем нелинейных уравнений предназначена функция fsolve() из пакета Optimization Toolbox, которая использует для решения метод наименьших квадратов и, в отличие от функции fzero(), ищет не только точки пересечения, но и точки касания графиков функций. Синтаксис функции:

fsolve( @fun, x0, options) — возвращает уточненное значение начального приближения х0, при котором достигаются нули функций описанных в fun, используя параметры вычислений из вектора options;

fsolve (@fun,[xl x2], options) — возвращает значение х, при котором достигаются нули функций описанных в fun, с заданием интервала поиска с помощью вектора x=[xl х2].

Применим функцию fsolve() для решения следующей системы нелинейных уравнений: .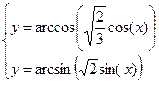

Сначала получим графическое решение заданной системы, используя следующую последовательность команд:

>> x=-1:0.1:1;

>> y1=acos(sqrt(2/3).*cos(x));

>> y2=asin(sqrt(2).*sin(x));

>> plot(x,y1,x,y2)

Результат представлен на рис. 5.8.

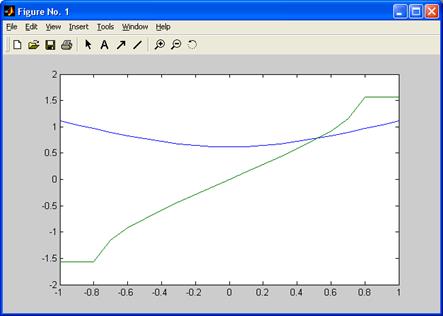
Рис. 5.8. Графическое решение системы уравнений.

Далее создадим m-файл fun.m, листинг которого представлен ниже:

function [ f]=fun1_(x)

f=[acos(sqrt(2/3)*cos(x(1)))-x(2); asin(sqrt(2)*sin(x(1)))-x(2)];

Найдем решение заданной системы нелинейных уравнений с точностью 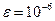, используя функцию fsolve():

x=fsolve (@fun,[0 0],optimset('tolX', 10^(-6)'))

В результате получим следующее решение:

x=[0.5236 0.7854]

5.2. Практическое задание 1

Используя теорему Кронекера-Капелли, исследовать СЛАУ, заданную в варианте, на совместность.

Решить СЛАУ следующими способами:

· матричным методом;

· методом Крамера;

· методом Гаусса с частичным выбором главного элемента;

· методом наименьших квадратов;

· с помощью функции mldivide().

ВАРИАНТЫ

№ варианта	Матрица коэффициентов системы А	Столбец свободных членов b

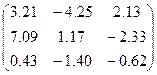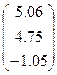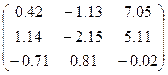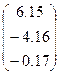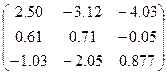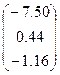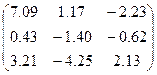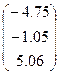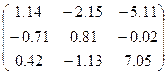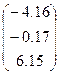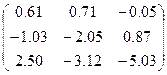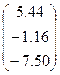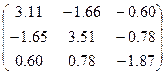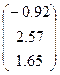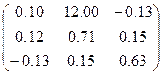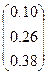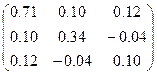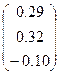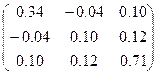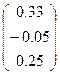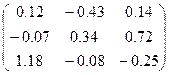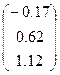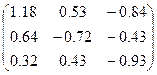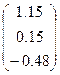5.3. Практическое задание 2

Отделить корни алгебраического или трансцендентного уравнения f(x)=0, построив график функции f(x).Найти решение уравнений с заданной точностью .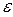

ВАРИАНТЫ

№ вар-та		Уравнение

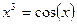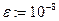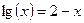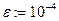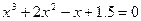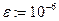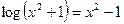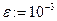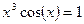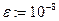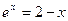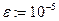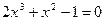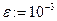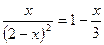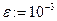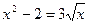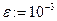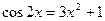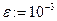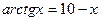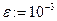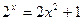5.4. Практическое задание 3

Построить графическое решение системы уравнений и, если графики пересекаются, найти численное решение с точностью .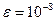

ВАРИАНТЫ

№ вар-та	Система уравнений

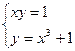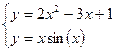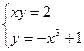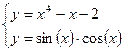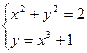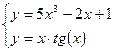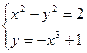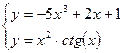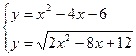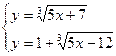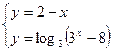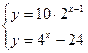5.5. Контрольные вопросы.

1. Какие команды очищают экран и помещают курсор в левый верхний угол окна командного режима работы?
2. С помощью какого знака можно перенести часть выражения на новую строку?

3. С помощью какого расширения MATLAB может выполнять символьные вычисления?

4. Какие основные системные переменные применятся в системе MATLAB?

1. Что такое Simulink и каково ее назначение?

6. Для чего нужны команды who и whos?

1. Какая функция служит для создания единичной матрицы?
2. Что выполняют команды ones(m, n) и zeros(m, n)?
3. Что выполняет команда rand(m, n)?
4. Какой будет матрица С после выполнения следующих операций:

A =[2 4;3 5]; B=[8 7;9 0]; C=cat(1,A,B)

1. Какой будет результат после выполнения следующей операции:

М=[3 1 4; 8 3 2; 8 1 1]

tril(M)

1. Какие цветовые выделения использует редактор/отладчик при выполнении синтаксического контроля программного кода?
2. Как проверить совместность системы линейных уравнений?

14. Как найти обратную матрицу ?

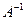15. В чем состоит матричный метод и почему данный метод не применяется на практике?

1. В чем состоит решение СЛАУ по методу Крамера и какая функция при этом используется?
2. В чем состоит решение СЛАУ по методу Гаусса и какая функция при этом используется?
3. Что возвращает функция lsqr(A, B, tol)?
4. Что вычисляется с помощью функции feval() и чему равно например,

fe=@exp. feval (fe,1,0))?

1. Для чего предназначены и чем отличаются функции fsolve() и fzero()?

21. Что рекомендуется делать для приближенного определения корней и интервалов, в пределах которых они находятся?