Использование статистических функций для решения маркетинговых задач

Использование статистических функций для решения маркетинговых задач

Задание 1.

На основании данных за 16 периодов об объемах продаж и затрат на рекламу некоторой фирмы, а также индексе потребительских расходов, представленных в таблице 1, выполните следующие задания:

1. Постройте диаграмму рассеивания (корреляционное поле), для переменных Объем продаж (Y) и Индекс потребительских расходов (Х₂)

§ Для построения диаграммы используйте Тип – Точечная.

§ На основании формы облака точек предположите, какая существует тенденция прямой линейной связи между переменными Х₂ и Y

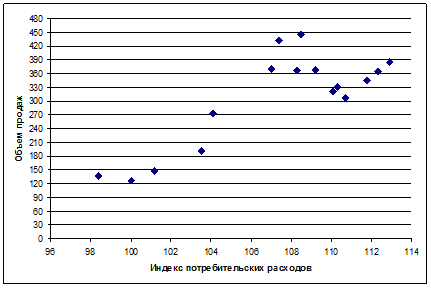
2. Определите степень влиянияиндекса потребительских расходовна объем продаж (вычислите коэффициент парной корреляции).

§ Для вычисления корреляции используйте статистическую функцию КОРРЕЛ(массив1;массив2;..), указав значения двух столбцов Объем продаж и Индекс потребительских расходов .

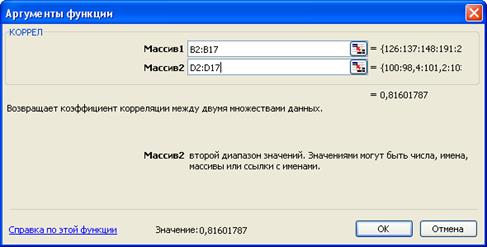
3. Оцените значимость вычисленного коэффициента парной корреляции.

§ Оценить значимость коэффициента корреляции можно, рассчитав критерий Стьюдента. Для этого вычислите критическое значение
t-статистики с помощью функции =СТЬЮДРАСПОБР().
В качестве аргументов задайте число степеней свободы, равное n-2 (т.е. 14) и вероятность (уровень значимости) равной a=0,1 (табличное значение).

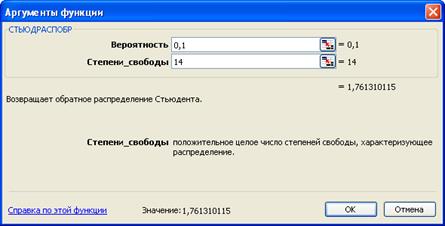
§ Если фактическое значение t-статистики по модулю больше критического, то с вероятностью (1-a) коэффициента корреляции отличается от нуля.

4. Постройте матрицу коэффициентов парной корреляции по трем переменным.

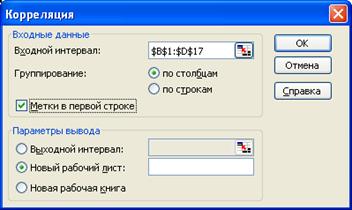
§ Для вычисления матрицы коэффициентов парной корреляции R, используйте инструмент Корреляция. Предварительно выполните команду:
Сервис->Надстройки-> Пакет анализа ->Корреляция.

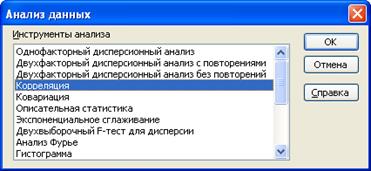
§ В диалоговом окне Корреляция установите параметры анализа – выделите диапазон данных Объем продаж, Затраты на рекламу и Индекс потребительских расходов. Установите флажки Группировка по столбцам, Метки в первой строке и Новый рабочий лист

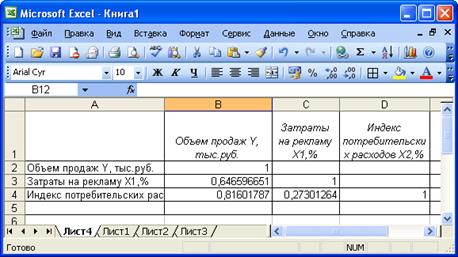
В результате получите матрицу коэффициентов парной

5. Сделайте выводы

Таблица 1.

	Объем продаж Y, тыс.руб.	Затраты на рекламу Х1,%	Индекс потребительских расходов Х2,%
1.
2.		4,8	98,4
3.		3,8	101,2
4.		8,7	103,5
5.		8,2	104,1
6.		9,7
7.		14,8	107,4
8.		18,7	108,5
9.		19,8	108,3
10.		10,6	109,2
11.		8,6	110,1
12.		6,5	110,7
13.		12,6	110,3
14.		6,5	111,8
15.		5,8	112,3
16.		5,7	112,9

Анализ и прогнозирование на основе многофакторных моделей

Задание 2.

Имеются статистические данные об одном из товаров фирмы (Таблица 2). Постройте модель для предсказания объема реализации данного товара.

Таблица 2

Объем реализации товара, млн. руб. Y	Месяц X1	Расходы на рекламу, тыс.руб X2.	Цена товара, руб. X3	Средняя цена товара у конкурентов, руб. X4	Индекс потребительских расходов % Х5,
	1.
	2.	4,8	14,8	17,3	98,4
	3.	3,8	15,2	16,8	101,2
	4.	8,7	15,5	16,2	103,5
	5.	8,2	15,5		104,1
	6.	9,7
	7.	14,8	18,1	20,2	107,4
	8.	18,7		15,8	108,5
	9.	19,8	15,8	18,2	108,3
	10.	10,6	16,9	16,8	109,2
	11.	8,6	16,3		110,1
	12.	6,5	16,1	18,3	110,7
	13.	12,6	15,4	16,4	110,3
	14.	6,5	15,7	16,2	111,8
	15.	5,8		17,7	112,3
	16.	5,7	15,1	16,2	112,9

Решение

1. Выберите факторные признаки для построения двухфакторной регрессионной модели:

Эндогенная переменная Y (зависимая, результирующая) – Объем реализации

Экзогенные переменные (независимые, объясняющие, факторные признаки):

- Время Х₁,

- Расходы на рекламу Х₂,

- Цена товара Х₃,

- Средняя цена товара у конкурентов Х₄,

- Индекс потребительских расходов Х₅

§ Для проведения корреляционного анализа используйте инструмент пакета анализа Excel – Корреляция.

§ Постройте матрицу коэффициентов парной корреляции.

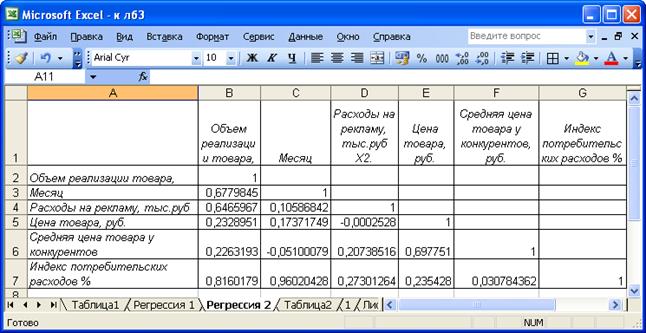
§ Выполните анализ матрицы коэффициентов.

Обратите внимание, что зависимая переменная Объем реализации имеет тесную связь с индексом потребительских расходов, с расходами на рекламу и временем.

Тесная связь факторов Время Х₁ и Индекс потребительских расходов Х₅ свидетельствует о наличии мультиколлинеарности^[1] (сравните коэффициенты корреляции). Для уменьшения мультиколлинеарности можно из двух экзогенных переменных, имеющих коэффициент парной корреляции >0,8, одну исключить из рассмотрения.

§ Из этих переменных в модели оставьте Х_5.

Для данного примера n=16, m=5, после исключения незначимых факторов n=16, факторов остается 2 (k=2).

Задача 3.

Большая сеть супермаркетов желает установить влияние рекламной компании на относительную конкурентоспособность. В 15 странах получены данные о затратах на рекламу относительно главного конкурента (затраты конкурента = 100) и о продажах относительно этого конкурента (продажи конкурента = 100):

Таблица 4.

Страна	Затраты на рекламу	Продажи

1. Определите зависимость между относительными затратами на рекламу и относительными продажами.

2. Постройте график относительных продаж (по оси у) относительных затрат на рекламу (ось х).

3. Выполните регрессионный анализ зависимости относительных продаж от затрат на рекламу.

4. Объясните смысл и значимость коэффициентов регрессии.

5. Определите какими должны быть относительные продажи компании, если фирма обеспечивает уровень затрат на рекламу, соответствующий конкуренту (если относительные затраты на рекламу составили 100).

6. Используя построенную модель, определите, в какой стране получен наилучший и наихудший результат.

Задача 4.

Имеется 20 фирм, по каждой из которых известны данные о затратах на реrламу сервисе и количестве туристов, воспользовавшихся услугами фирмы:

Таблица 5

Фирма	Затраты на рекламу	Количество туристов

1. Постройте диаграмму рассеяния (корреляционное поле) для переменных Затраты на рекламу и Количество туристов.

2. Постройте уравнение парной регрессии и проверьте качество построенного уравнения.

3. Дайте экономическую интерпретацию коэффициентам уравнения регрессии

4. Постройте график прогноза количества туристов, если прогнозное значение затрат на рекламу в ближайшем периоде составит 110% от их последнего значения.

Задача 5.

Туристическую фирму интересует связь между числом отпускников, останавливающихся в гостиницах, и расходами на рекламу гостиниц. За сезон была собрана следующая информация

Таблица 6

Гостиница
Реклама, тыс.руб.
Число гостей

1. Постройте модель зависимости количества гостей от затрат на рекламу.

2. Поясните значения параметров уравнения регрессии.

3. Рассчитайте прогнозное значение результатов результата, если прогнозное значение фактора Х составляет 80% от его максимального значения.

4. Постройте график, отобразив прогнозные значения на 2 будущих периода.

5. Определите, в какой гостинице число гостей значительно ниже предсказанного по модели.

Нелинейная регрессия

При изучении зависимости экономических показателей на основе реальных статистических данных, чаще встречаются нелинейные зависимости. Например, затухающие гармонические или негармонические колебания могут характеризовать объемы продаж сезонного товара на этапе ухода с рынка. Зависимости могут быть представлены кусочно-линейной функцией, которая на разных участках области определения может быть задана разными аналитическими выражениями.

Два класса нелинейных процессов:

1. Нелинейные относительно независимых переменных, но линейные по оцениваемым параметрам.

Данный тип регрессии включает уравнения, в которых зависимая переменнаялинейно связана с параметрами:

– Полиномы разных степеней:

y_i=a₀+a₁x_i+ a₂x²_i+…a_kx^k_i+e_i

При оценке параметров регрессий нелинейных по независимым переменным, используется метод замены переменных. Нелинейные независимые переменные заменяются новыми линейными, и нелинейная регрессия сводится к линейной.

– Равносторонняя гипербола

y_i=a+b/x_i+e_i

Для оценки параметров также применяется метод замены переменных (1/х заменяют на переменную z). Равносторонняя гипербола применяется для характеристики связи удельных расходов сырья, материалов и топлива, выпускаемой продукции. Также примером использования равносторонней гиперболы являются кривые Филлипса[4] и Энгеля[5].

2. Нелинейные по оцениваемым параметрам.

Примерами таких регрессий являются функции:

– степенная y= ax^b;

– показательная y=ab^x;

^– экспоненциальная y=e^a+bx.

Для приведения таких моделей к линейному виду выполняется логарифмирование или замена переменных.

Например, степенная функция y= ax^b – регрессия, нелинейная по параметрам, но внутренне линейная. Используется при изучении зависимости спроса от цены. Логарифмирование уравнения по основанию приводит его к линейному виду:

lny=lna+blnx

Задание 1.

На основании данных таблицы 1, постройте модель зависимости объема выпускаемой продукции от температуры при технологическом процессе помощью полинома второй степени y_i=a₀+a₁x_i+ a₂x²_i+e_i

Таблица 1

Температура Х (0С)
Объем выпуска продукции Y, шт

Решение

1. Постройте график точечной зависимости объема выпуска продукции от температуры.

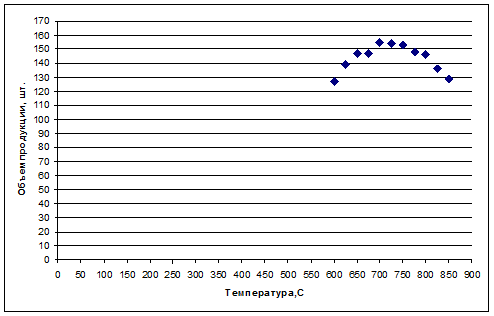
2. Введите новую переменную Z (z_i= x²_i ).

Получите двухфакторное уравнение: y_i=a₀+a₁x_i+ a₂z_i +e_i

3. Рассчитайте значения z_i= x²_i

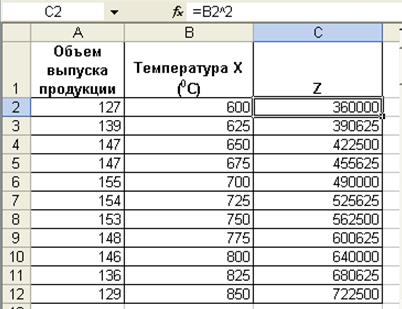
4. Для оценки коэффициентов уравнения выполните команду Сервис->Надстройки-> Пакет анализа ->Регрессия.

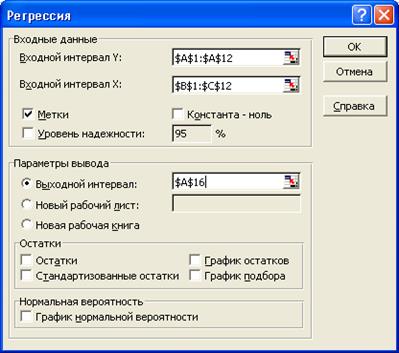
5. Запишите уравнение регрессии и оцените коэффициенты

6. Постройте график для полученной модели.

Задание 2.

На основании информации о норме безработицы и темпах инфляции (Таблица 2), постройте:

– Диаграмму рассеяния

– Модель регрессии зависимости темпов инфляции от нормы безработицы[6].

– Отобразите результаты расчетов на графике.

Таблица 2

Темпы инфляции Y		1,1	1,2	1,3	1,7	2,9	2,9	4,2	5,4
Норма безработицы Х	6,5	5,4	5,5	5,0	4,4	3,7	3,7	3,5	3,4

Решение

1. Постройте диаграмму рассеяния для наглядного отображения нелинейной связи между рассматриваемыми переменными.

2. Подберите линию тренда, наилучшим образом соответствующую характеру статистических данных.

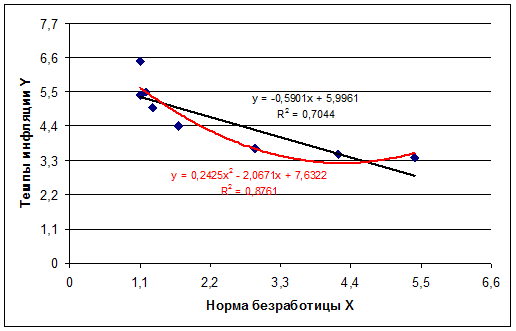
3. Расположение исходного набора точек напоминает график обратной пропорциональной зависимости.

4. Рассчитайте значение z_i =1/x_i

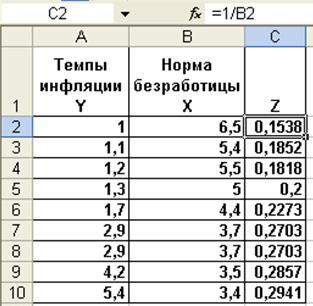
5. Рассмотрите модель равносторонней гиперболы y_i=a+b/x_i+e_i, соответствующую линейной связи между переменными Y и Z:

y_i=a₀+a₁z_i +e_I, где z_i=1/x_i

6. Для оценки коэффициентов уравнения выполните команду Сервис->Надстройки-> Пакет анализа ->Регрессия.

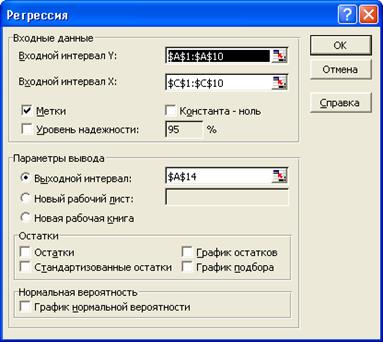
7. Запишите уравнение регрессии на основе отчета инструмента Регрессия

8. Постройте график для полученной модели.

Задание 3

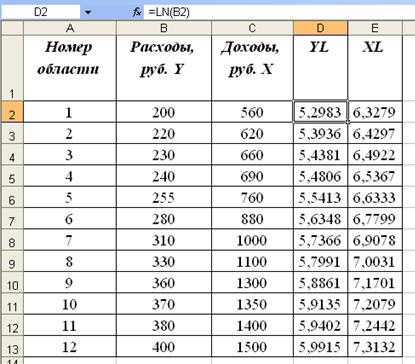
По 12 областям информация, характеризующая зависимость потребительских расходов Y душу населения от денежных расходов Х (Таблица 3).

Таблица 3.

Номер области	Расходы, руб. Y	Доходы, руб. Х
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.

1. Постройте степенную модель.

2. Оцените модель, определив индекс корреляции, среднюю относительную ошибку и коэффициент детерминации.

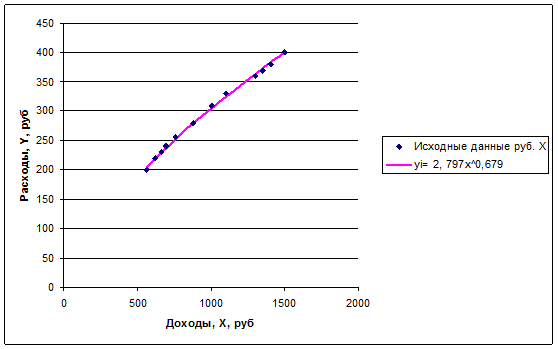
3. Постройте графики для исходных данных и полученной модели

Решение.

1. Уравнение степенной модели имеет вид y= ax^b

Выполните логарифмирование обеих частей уравнения lny_i=lna+blnx_i

Обозначьте YL=lny, XL=lna, AL=blnx

Уравнение примет линейный вид YL=AL+bXL

2. Для оценки коэффициентов уравнения выполните команду Сервис->Надстройки-> Пакет анализа ->Регрессия.

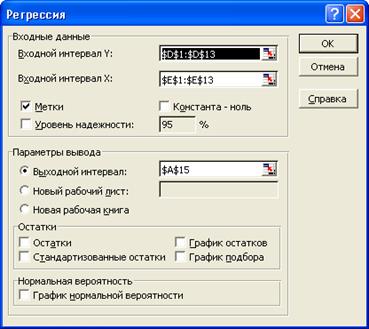
3. Запишите уравнение регрессии на основе протокола инструмента Регрессия

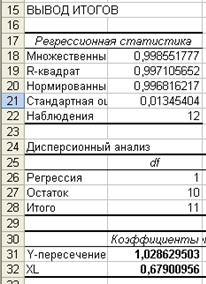
4. Прейдите к исходным переменным X и Y, выполнив потенцирование данного уравнения: y= е^1,0286x^0,679

Значение параметра а = е^1,0286 получите с помощью функции Excel exp(), а =2, 797.

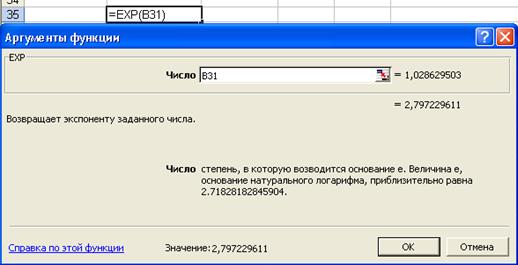
Получите уравнение степенной модели регрессии: y_i= 2, 797x^0,679

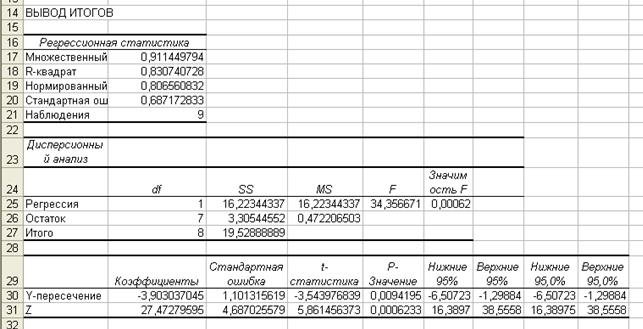
5. Из протокола инструмента Регрессия определите:

– Индекс корреляции. Каков уровень связи между переменными X и Y

– Коэффициент детерминации. На сколько процентов вариация результата Y (потребительские расходы), объясняется вариацией фактора Х (денежные доходы)?

6. Постройте график для полученной модели.

[1] Мультиколлинеарность – высокая взаимная коррелированность экзогенных переменных, которая приводит к линейной зависимости нормальных уравнений (может возникать, например, если несколько независимых переменных могут иметь общий временной тренд, относительно которого они совершают малые колебания).

Мультиколлинеарность в исходных данных считают установленной, если коэффициент парной корреляции между переменными >0,8.

[2] Эластичность Y по отношению к Xj определяется как процентное изменение Y, отнесенное к соответствующему процентному изменению X. В общем случае эластичности не постоянны, они различаются, если измерены для различных точек на линии регрессии. Высокий уровень эластичности означает сильное влияние независимой переменной на зависимую.

[3] Бета-коэффициент показывает, на какую часть величины среднеквадратическое отклоненияS_у изменится зависимая переменная Y, если соответствующая независимая переменнаяX_j изменится на величину своего среднеквадратическое отклонения при фиксированном значении остальных независимых переменных.

[4] Кривая Филипса показывает взаимное изменение уровней безработицы и инфляции в экономике (инфляция высока при низкой безработице и низка – при высокой).

[5] Кривая Энгеля показывает величину расходов на товары в зависимости от роста дохода. Закон Энгеля устанавливает, что доля расходов на продовольственные товары по мере роста дохода падает, т.к. продукты питания относятся к необходимым товарам. Кривая Энгеля полена при определении степени влияния на спрос дохода и изменений в относительных ценах.

[6] Норма безработицы – доля безработных в общей численности рабочейсилы.

Использование статистических функций для решения маркетинговых задач

Задание 1.

На основании данных за 16 периодов об объемах продаж и затрат на рекламу некоторой фирмы, а также индексе потребительских расходов, представленных в таблице 1, выполните следующие задания:

1. Постройте диаграмму рассеивания (корреляционное поле), для переменных Объем продаж (Y) и Индекс потребительских расходов (Х₂)

§ Для построения диаграммы используйте Тип – Точечная.

§ На основании формы облака точек предположите, какая существует тенденция прямой линейной связи между переменными Х₂ и Y

2. Определите степень влиянияиндекса потребительских расходовна объем продаж (вычислите коэффициент парной корреляции).

§ Для вычисления корреляции используйте статистическую функцию КОРРЕЛ(массив1;массив2;..), указав значения двух столбцов Объем продаж и Индекс потребительских расходов .

3. Оцените значимость вычисленного коэффициента парной корреляции.

§ Оценить значимость коэффициента корреляции можно, рассчитав критерий Стьюдента. Для этого вычислите критическое значение
t-статистики с помощью функции =СТЬЮДРАСПОБР().
В качестве аргументов задайте число степеней свободы, равное n-2 (т.е. 14) и вероятность (уровень значимости) равной a=0,1 (табличное значение).

§ Если фактическое значение t-статистики по модулю больше критического, то с вероятностью (1-a) коэффициента корреляции отличается от нуля.

4. Постройте матрицу коэффициентов парной корреляции по трем переменным.

§ Для вычисления матрицы коэффициентов парной корреляции R, используйте инструмент Корреляция. Предварительно выполните команду:
Сервис->Надстройки-> Пакет анализа ->Корреляция.

§ В диалоговом окне Корреляция установите параметры анализа – выделите диапазон данных Объем продаж, Затраты на рекламу и Индекс потребительских расходов. Установите флажки Группировка по столбцам, Метки в первой строке и Новый рабочий лист

В результате получите матрицу коэффициентов парной

5. Сделайте выводы

Таблица 1.

	Объем продаж Y, тыс.руб.	Затраты на рекламу Х1,%	Индекс потребительских расходов Х2,%
1.
2.		4,8	98,4
3.		3,8	101,2
4.		8,7	103,5
5.		8,2	104,1
6.		9,7
7.		14,8	107,4
8.		18,7	108,5
9.		19,8	108,3
10.		10,6	109,2
11.		8,6	110,1
12.		6,5	110,7
13.		12,6	110,3
14.		6,5	111,8
15.		5,8	112,3
16.		5,7	112,9