Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами.

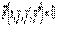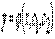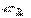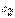Дифференциальное уравнение второго порядка имеет вид Определение. Общим решением уравнения второго порядка называется такая функция , которая при любых значениях и является решением этого уравнения. Определение. Линейным однородным уравнением второго порядка называется уравнение 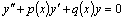. Если коэффициенты 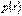и 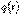постоянны, т.е. не зависят от , то это уравнение называют уравнением с постоянными коэффициентами и записывают его так: 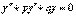. Уравнение 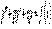будем называть линейным неоднородным уравнением. Определение.Уравнение 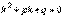, которое получается из линейного однородного уравнения заменой функции 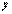единицей, а 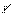и 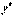- соответствующими степенями 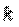, называется характеристическим уравнением.

1. Множества. Операции над множествами.

2. Действительные числа и числовая ось.
3. Числовые промежутки. Окрестность точки.
4. Числовые функции. График функции. Способы задания функций

5. Основные характеристики функции (монотонность, четность-нечетность, периодичность)

6. 0братная функция, сложная функция .
7. Основные элементарные функции и их графики. Степенные функции.

8. Основные элементарные функции и их графики. Показательные функции.

9. Основные элементарные функции и их графики. Логарифмические функции.

10. Основные элементарные функции и их графики. Тригонометрические функции

11. Основные элементарные функции и их графики. Обратные тригонометрические функции

12. Числовая последовательность. Предел числовой последовательности

13. Предел функции. Определения. Основные теоремы о пределах
14. Бесконечно большая функция (б.б.в.). Бесконечно малые функции (б.м.в.). Основные теоремы
15. Первый замечательный предел. Второй замечательный предел
16. Эквивалентные бесконечно малые функции. Таблица эквивалентных величин
17. Непрерывность функций в точке. Основные определения. Непрерывность функции на множестве
18. Точки разрыва функции I-го рода
19. Точки разрыва функции II-го рода

20. Основные теоремы о непрерывных функциях. Непрерывность элементарных функций

21. Производная функции. Определение производной; ее механический и геометрический смысл.

22 Уравнение касательной и нормали к кривой
23. Связь между непрерывностью и дифференцируемостью функции
24. Производная суммы, разности, произведения и частного функций
25. Производная сложной и обратной функций.

26. Дифференцирование неявных и параметрически заданных функций
27. Производные основных элементарных функций
28. Производные высших порядков
29. Дифференциал функции
30. Понятие дифференциала функции
31. Основные теоремы о дифференциалах
32. Таблица дифференциалов
33. Применение дифференциала к приближенным вычислениям
34. Дифференциалы высших порядков
35. Некоторые теоремы о дифференцируемых функциях (Ферма, Ролля, Лагранжа и Коши)
36. Правила Лопиталя
37.Связь между дифференцируемостью и монотонностью функции
38. Экстремумы функций. Определение. Необходимое условие существования экстремума

39. I-е и II-едостаточные условия существования экстремума
40. Наибольшее и наименьшее значения функции на отрезке
41. Выпуклость графика функции. Связь с производной II-гопорядка

42. Точки перегиба. Необходимое условие существования точки перегиба

43. Достаточное условие существования точки перегиба
44. Асимптоты графика функции
45. Общая схема исследования функции и построения графика
46. Понятие неопределенного интеграла

47. Свойства неопределенного интеграла
48. Таблица основных неопределенных интегралов

49. Основные методы интегрирования (метод интегрирования подстановкой)
50. Основные методы интегрирования (метод интегрирования по частям)

51. Простейшие дроби четырех типов

52.Интегрирование рациональных функций
53. Интегрирование тригонометрических функций. Универсальная подстановка.
54. Интегрирование простейших иррациональных функций
55. Определенный интеграл как предел интегральной суммы

56. Теорема существования определенного интеграла

57. Геометрический смысл определенного интеграла

58. Основные свойства определенного интеграла

59. Оценка определенного интеграла. Теорема о среднем
60. Вычисления определенного интеграла. Формула Ньютона-Лейбница

61. Интегрирование подстановкой (заменой переменной) в определенном интеграле
62. Интегрирование по частям в определенном интеграле

63. Несобственные интегралы. Интеграл с бесконечным промежутком интегрирования (несобственный интеграл I рода)

64. Несобственные интегралы. Интеграл от разрывной функции (несобственный интеграл II рода)

65. Приложения определенного интеграла. Вычисление площадей плоских фигур
66. Приложения определенного интеграла. Вычисление длины дуги плоской кривой
67. Приложения определенного интеграла. Вычисление объема тела
68. Функции нескольких (двух) переменных. Основные понятия

69. Предел функции двух переменных
70. Непрерывность функции двух переменных
71. Производные и дифференциалы функции нескольких переменных

72. Применение дифференциала функции нескольких(двух) переменных к приближенным вычислениям
73. Частные производные первого порядка

74. Производная по направлению. Градиент.

75. Экстремум функции нескольких переменных.

76. Условный экстремум. Метод множителей Лагранжа.

77. Числовые ряды. Основные понятия. Сходимость ряда.

78. Необходимый признак сходимости. Гармонический ряд.

79. Ряды с положительными членами.

80. Достаточные признаки сходимости рядов с положительными членами.

81. Знакочередующиеся ряды. Абсолютная и условная сходимости.

82. Признак Лейбница.

83. Степенные ряды. Область сходимости степенного ряда.

84. Теорема Абеля. Интервал и радиус сходимости.

85. Ряды Тейлора и Маклорена.

86.Разложение в ряд Маклорена функций ln(1+x), cos x.

87. Разложение в ряд Маклорена функций e^x , sin x.

88. Применение рядов в приближенных вычислениях.

89. Двойные интегралы. Основные понятия и определения.

90.Основные свойства двойного интеграла.

91.Основные свойства двойного интеграла.

92. Вычисление двойного интеграла в декартовых координатах.

93. Приложения двойного интеграла.

94. Дифференциальные уравнения. Основные понятия.

95. Дифференциальные уравнения первого порядка. Теорема о существовании и единственности решения.

96. Дифференциальные уравнения с разделяющимися переменными.

97. Однородные дифференциальные уравнения первого порядка.

98. Линейные дифференциальные уравнения первого порядка.

99. Дифференциальные уравнения второго порядка, допускающие понижение порядка.

100. Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами.