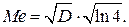Распределение Вейбулла-Гнеденко

В своих работах Вейбулл использовал это распределение для описания экспериментально наблюдавшихся разбросов усталостной прочности стали, пределов ее упругости, размеров частиц копоти и др. Также распределение Вейбулла может быть использовано для изучения разброса сроков службы радиоэлектронной аппаратуры.

В частности, этому распределению удовлетворяют:

- наработка деталей по усталостным разрушениям;

- наработка подшипников до отказа;

- наработка деталей и узлов автомобилей, подъемно-транспортных машин;

- наработка конденсаторов;

- наработка реле.

Плотность вероятности наработки до отказа:

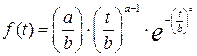
Функция распределения времени наработки до отказа:

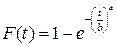
Вероятность безотказной работы:

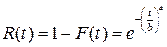
Интенсивность отказов (функция «опасности»):

,

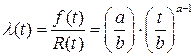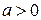где — время, — параметр формы, 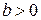— параметр масштаба.

Соотношения между моментами и параметрами распределения:

Математическое ожидание (среднего времени наработки до отказа — T):

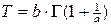
Дисперсия D и среднеквадратическое отклонение :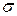

;

.

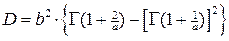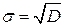Коэффициент асимметрии Sk («скос» — skewness):

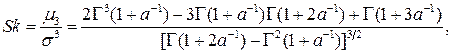
Коэффициент эксцесса Ex («островершинность» — excess):

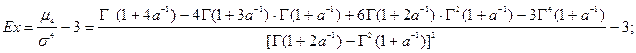
Гамма-процентная наработка до отказа:

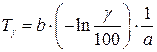
Мода распределения:

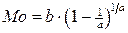
Медиана распределения:

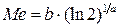
95-процентный квантиль :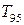

.

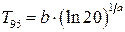Коэффициент вариации:

;

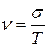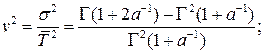и при известном значении 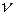мы приходим к необходимости решения уравнения:

для определения параметра формы распределения,

где 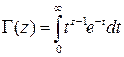— функция Эйлера (эйлеров интеграл 2-го рода).

Заметим, что коэффициенты асимметрии и островершинности не зависят от параметра масштаба b.

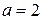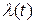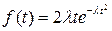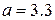Универсальность распределения Вейбулла объясняется следующим: при распределение превращается в экспоненциальное; при функции плотности и интенсивности отказов убывающие; при интенсивность отказов возрастающая; при функция линейная, и распределение Вейбулла превращается в распределение Рэлея с плотностью , при распределение Вейбулла близко к нормальному. Наряду с логарифмически нормальным распределением, оно хорошо описывает наработку деталей по усталостным разрушениям, наработку до отказа подшипников, а также используется для оценки надежности деталей и узлов машин, в частности автомобилей, подъемно-транспортных и других машин.

Распределение Релея

Распределение Релея вытекает из распределения Вейбулла-Гнеденко при .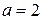

Плотность вероятности наработки до отказа:

,

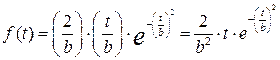
где ; .

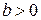Введя переобозначения 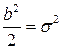, плотность вероятности можно представить в виде

.

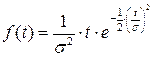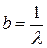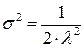Если принять , то , и 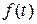принимает вид .

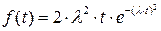Функция распределения времени наработки до отказа:

.

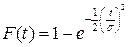Вероятность безотказной работы:

.

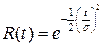Интенсивность отказов:

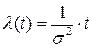
Соотношения между моментами и параметрами распределения:

Среднее время наработки до отказа T:

.

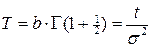Дисперсия D:

.

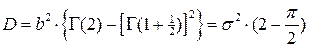Коэффициент асимметрии Sk:

.

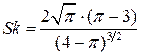Коэффициент островершинности Ex:

.

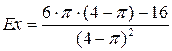Коэффициент вариации ν:

.

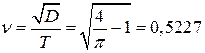Мода:

.

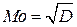Медиана: