Напряжения и перемещения при изгибе.
Гипотезы при изгибе. Нейтральный слой, радиус кривизны, кривизна, распределение деформаций и нормальных напряжении по высоте поперечного сечения стержня. Касательные напряжения при плоском поперечном изгибе стержней. Расчет балок на прочность при изгибе. Перемещения при изгибе.
Нормальные напряжения при чистом прямом изгибе. Так как нормальные напряжения зависят только от изгибающих моментов, то вывод формулы для вычисления  можно производить применительно к чистому изгибу. Отметим, что методами теории упругости можно получить точную зависимость для нормальных напряжений при чистом изгибе, если же решать эту задачу методами сопротивления материалов, необходимо ввести некоторые допущения.
можно производить применительно к чистому изгибу. Отметим, что методами теории упругости можно получить точную зависимость для нормальных напряжений при чистом изгибе, если же решать эту задачу методами сопротивления материалов, необходимо ввести некоторые допущения.
Таких гипотез при изгибе три:
1) гипотеза плоских сечений (гипотеза Бернулли) -
сечения плоские до деформации остаются плоскими и после деформации, а лишь поворачиваются относительно некоторой линии, которая называется нейтральной осью сечения балки. При этом волокна балки, лежащие с одной стороны от нейтральной оси будут растягиваться, а с другой - сжиматься; волокна, лежащие на нейтральной оси своей длины не изменяют;
2) гипотеза о постоянстве нормальных напряжений - напряжения, действующие на одинаковом расстоянии у от нейтральной оси, постоянны по ширине бруса;
3) гипотеза об отсутствии боковых давлений - соседние продольные волокна не давят друг на друга.
Статическая задача о плоском изгибе. Изгибающий момент в сечении представляет собой сумму моментов всех элементарных внутренних нормальных сил 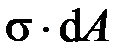 , возникающих на элементарных площадках поперечного сечения балки, относительно нейтральной оси
, возникающих на элементарных площадках поперечного сечения балки, относительно нейтральной оси
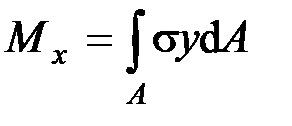 .
.
Данное выражение представляет собой статическую сторону задачи о плоском изгибе. Но его нельзя использовать для определения нормальных напряжений, так как неизвестен закон распределения напряжений по сечению.
 Геометрическая сторона задачи о плоском изгибе. Выделим двумя поперечными сечениями элемент балки длиной
Геометрическая сторона задачи о плоском изгибе. Выделим двумя поперечными сечениями элемент балки длиной 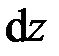 . Под нагрузкой нейтральная ось искривляется (радиус кривизны
. Под нагрузкой нейтральная ось искривляется (радиус кривизны 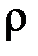 ), а сечения поворачиваются относительно своих нейтральных линий на угол
), а сечения поворачиваются относительно своих нейтральных линий на угол 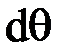 . Длина отрезка волокон нейтрального слоя при этом остается неизменной
. Длина отрезка волокон нейтрального слоя при этом остается неизменной
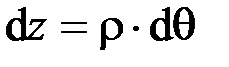 .
.
Определим длину отрезка волокон, отстоящего от нейтрального слоя на расстоянии 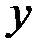
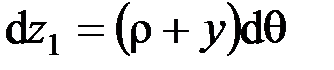 .
.
Относительное удлинение в этом случае будет
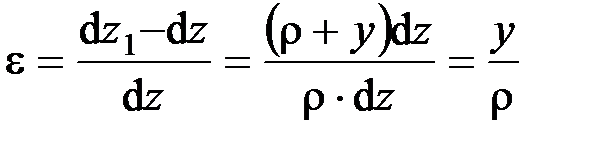 .
.
Зависимость 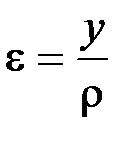 отражает геометрическую сторону задачи о плоском изгибе, из которой видно, что деформации продольных волокон изменяются по высоте сечения по линейному закону.
отражает геометрическую сторону задачи о плоском изгибе, из которой видно, что деформации продольных волокон изменяются по высоте сечения по линейному закону.
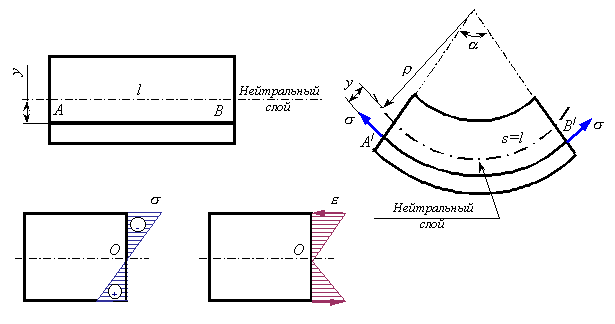
Совокупность волокон, не меняющих своей длины при изгибе балки, называется нейтральным слоем.
Линия, по которой поперечное сечение балки пересекается с нейтральным слоем балки, называется нейтральной линией сечения.
Физическая сторона задачи о плоском изгибе. Используя закон Гука при осевом растяжении, получаем
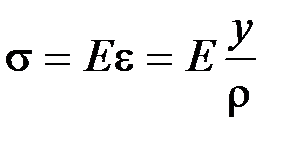 .
.
Подставив в выражение, отражающее статическую сторону задачи о плоском изгибе, значение  , получаем
, получаем
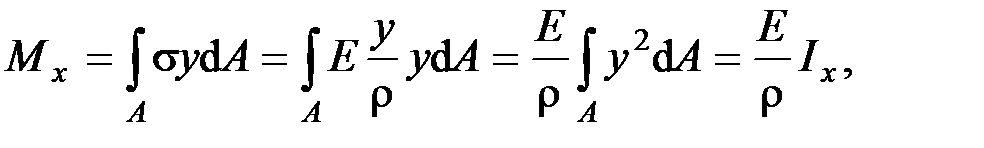
откуда 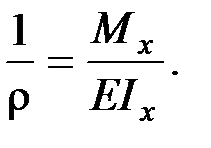
Подставив значение 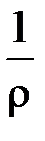 в исходную формулу, получаем
в исходную формулу, получаем
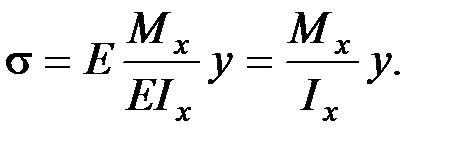
Данное выражение отражает физическую сторону задачи о плоском изгибе, которое дает возможность рассчитать нормальные напряжения по высоте сечения.
Хотя это выражение получено для случая чистого изгиба, но как показывают теоретические и экспериментальные исследования, оно может быть использовано и для плоского поперечного изгиба.
Нейтральная линия. Положение нейтральной линии определим из условия равенства нулю нормальной силы в сечениях балки при чистом изгибе
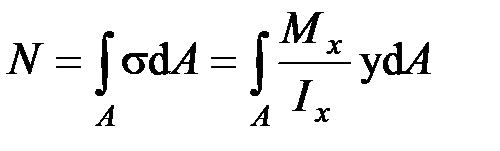 .
.
Так как 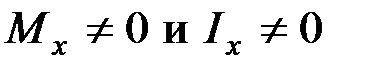 , то необходимо, чтобы нулю был равен интеграл
, то необходимо, чтобы нулю был равен интеграл 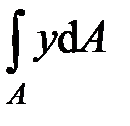 . Данный интеграл представляет собой статический момент сечения относительно нейтральной оси. Так как статический момент сечения равен нулю только относительно центральной оси, следовательно, нейтральная линия при плоском изгибе совпадает с главной центральной осью инерции сечения.
. Данный интеграл представляет собой статический момент сечения относительно нейтральной оси. Так как статический момент сечения равен нулю только относительно центральной оси, следовательно, нейтральная линия при плоском изгибе совпадает с главной центральной осью инерции сечения.
Касательные напряжения. Касательные напряжения, которые возникают в сечениях балки при плоском поперечном изгибе, определяются по зависимости:
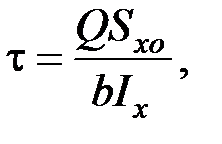
где 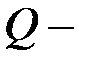 поперечная сила в рассматриваемом сечении балки;
поперечная сила в рассматриваемом сечении балки;
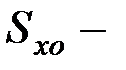 статический момент площади отсеченной части сечения относительно нейтральной оси балки;
статический момент площади отсеченной части сечения относительно нейтральной оси балки;
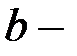 ширина сечения в рассматриваемом слое;
ширина сечения в рассматриваемом слое;
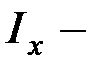 момент инерции сечения относительно нейтральной оси.
момент инерции сечения относительно нейтральной оси.
Касательные напряжения равны нулю в крайних волокнах сечения и максимальны в волокнах нейтрального слоя.
Расчет балок на прочность при изгибе. Прочность балки будет обеспечена, если будут выполняться условия:
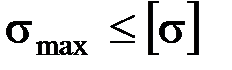 ;
; 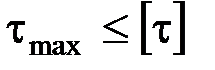 .
.
Максимальные нормальные напряжения при изгибе возникают в сечениях, где действует максимальный изгибающий момент, в точках сечения наиболее удаленных от нейтральной оси
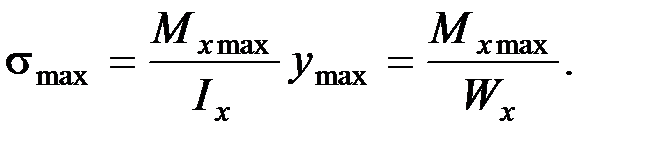
Максимальные касательные напряжения возникают в сечениях балки, где действует максимальная поперечная сила
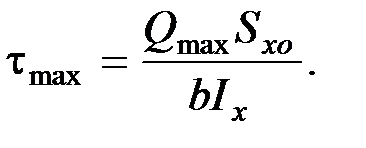
Касательные напряжения 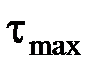 обычно малы по сравнению с
обычно малы по сравнению с 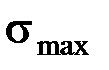 и в расчетах, как правило, не учитываются. Проверка по касательным напряжениям производится только для коротких балок.
и в расчетах, как правило, не учитываются. Проверка по касательным напряжениям производится только для коротких балок.
Перемещения при изгибе.
Под расчетом на жесткость понимают оценку упругой податливости балки под действием приложенных нагрузок и подбор таких размеров поперечного сечения, при которых перемещения не будут превышать установленных нормами пределов.
Условие жесткости при изгибе
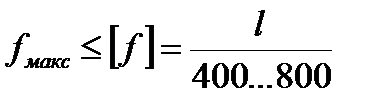
Перемещение центра тяжести сечения по направлению перпендикулярному к оси балки, называется прогибом. Угол, на который каждое сечение поворачивается по отношению к своему первоначальному положению - угол поворота.
Уравнение упругой линии балки
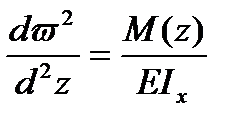
Существуют три метода решения дифференциального уравнения упругой линии балки. Это метод непосредственного интегрирования, метод Клебша и метод начальных параметров.
Метод непосредственного интегрирования
Проинтегрировав уравнение упругой линии балки первый раз, получают выражение для определения углов поворота:
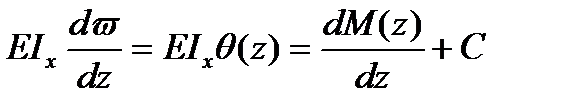
Интегрируя второй раз, находят выражения для определения прогибов:
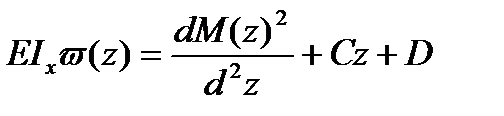
Значения постоянных интегрирования С и D определяют из начальных условий на опорах балки
Метод начальных параметров
Для углов поворота
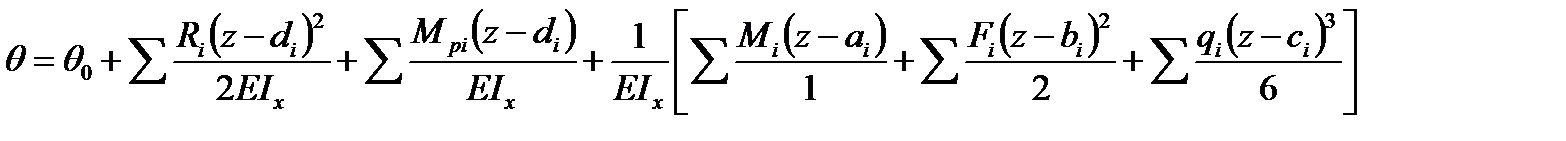
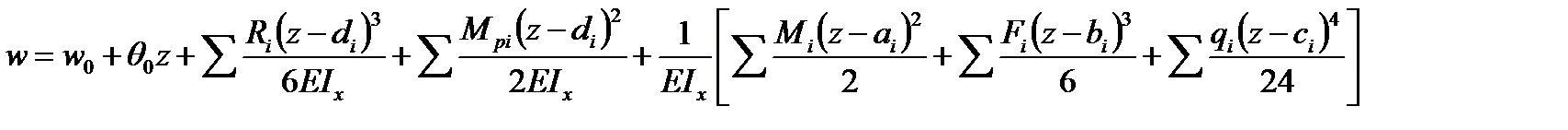 Для прогибов:
Для прогибов:
где Ө—угол поворота сечения, W—прогиб, Өo - угол поворота в начале координат, Wo—прогиб в начале координат.
Вычислений перемещений методом Мора.
Если не требуется знание уравнения изогнутой линии бруса, а необходимо определить только линейные или угловые перемещения отдельного сечения, удобнее всего воспользоваться методом Мора.
Формулу Мора можно получить, например. используя принцип возможных перемещений.
а) б)
Рис. 1
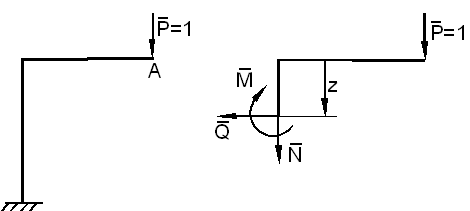
Рассмотрим схему (рис.1,а), когда в точке А в направлении искомого перемещения 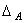 приложена единичная сила
приложена единичная сила 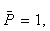 вызывающая в поперечном сечении системы внутренние силовые факторы
вызывающая в поперечном сечении системы внутренние силовые факторы 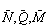 (рис. 1,б). В соответствии с принципом возможных перемещений работа этих внутренних силовых факторов на любых возможных перемещениях должна равняться работе единичной силы
(рис. 1,б). В соответствии с принципом возможных перемещений работа этих внутренних силовых факторов на любых возможных перемещениях должна равняться работе единичной силы 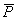 на возможном перемещении
на возможном перемещении 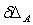 :
:
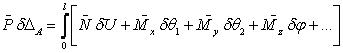
Выбираем возможные перемещения пропорциональными действительным:
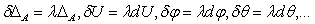
И после подстановки получим:
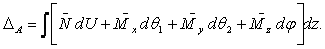
При учете, что
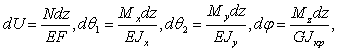
приходим к формуле Мора
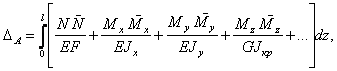 (1)
(1)
которая служит для определения любых обобщённых перемещений в стержневых системах.
В случае, когда брус работает только на изгиб (Mx  0, Nz = Mz = My = Qx = Qy = 0), выражение (1) принимает вид:
0, Nz = Mz = My = Qx = Qy = 0), выражение (1) принимает вид:
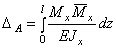 (2)
(2)
Правило Верещагина вычисления интегралов в формуле Мора. Справедливость правила Верещагина.
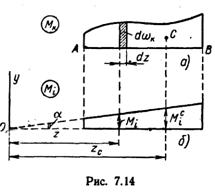
Рис.2
Приведены две эпюры изгибающих моментов, из которых одна Мк имеет произвольное очертание, а другая Мi прямолинейна (рис.2).
Сечение стержня считаем постоянным. В этом случае
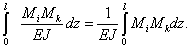
Величина Mκdz представляет собой элементарную площадь dω эпюры Мк (заштрихована). Получаем
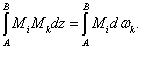
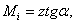 Но
Но
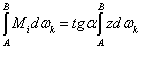 поэтому,
поэтому,
Выражение 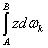 представляет собой статический момент площади эпюры Мк относительно оси у, проходящей через точку О, равный ωκΖc, где ωκ — площадь эпюры моментов; Ζс — расстояние от оси у до центра тяжести эпюры Мк. Из рисунка очевидно:
представляет собой статический момент площади эпюры Мк относительно оси у, проходящей через точку О, равный ωκΖc, где ωκ — площадь эпюры моментов; Ζс — расстояние от оси у до центра тяжести эпюры Мк. Из рисунка очевидно:
Ζc= Мiº/ tqα,
где Мºi — ордината эпюры Mi, расположенная под центром тяжести эпюры Мк (под точкой С).
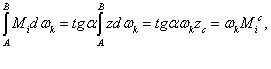 Μіº (3)
Μіº (3)
Формула (3) представляет правило вычисления интеграла Мора: интеграл равен произведению площади криволинейной эпюры на ординату, взятую с прямолинейной эпюры и расположенную под центром тяжести криволинейной эпюры.
Встречающиеся на практике криволинейные эпюры могут быть разбиты на ряд простейших: прямоугольник, треугольник, симметричную квадратичную параболу и т.п.
