Стержневые системы при растяжении-сжатии.
Понятие о стержневых системах и механизмах. Статически определимые и неопределимые стержневые системы: особенности расчёта. Механические свойства материалов. Типовые диаграммы деформирования материала при растяжении. Характеристики упругих, прочностных и деформационных свойств материалов. Назначение допускаемых напряжений, коэффициент запаса прочности. Условия прочности и жесткости конструкции.
Стержневые системы состоят из стержней, соединенных в узлах. Сооружения во время всего срока эксплуатации должны быть геометрически неизменяемыми системами, способными воспринимать нагрузки без заметного изменения геометрии. Положение шарнира на плоскости определяется двумя координатами. Следовательно, шарнир обладает двумя степенями свободы. Степень свободы - число независимых геометрических параметров, определяющих положение шарнира. Если шарнир присоединен к земле с помощью стержня, то эта система имеет одну степень свободы. Система с одной степенью свободы - геометрически изменяемая система. Узлы изменяемых систем могут перемещаться без изменения длин стержней. Траекторией движения шарнира является дуга окружности. Изменяемые системы называют механизмами.
При расчёте статически определимых стержневых систем (число неизвестных в задаче не должно превышать числа уравнений равновесия) для определения опорных реакций, внутренних усилий и деформаций достаточно использования уравнений статики.
Пример статически определимой системы: к двум одинаковым стержням приложена сила F. Определить усилия в стержнях.
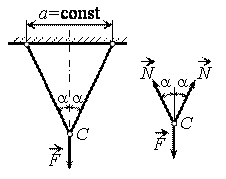
Р е ш е н и е.
Из условия равновесия узла С находим усилия в стержнях:
∑Yі = 0, 2Ncosα – F = 0 , N = F/ (2cosα) .
Статически неопределимая система. В качестве примера рассмотрим систему из трех стержней, нагруженных силой Q (рис.1). Длины крайних стержней обозначим 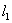 ; длину среднего
; длину среднего 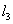 .
.
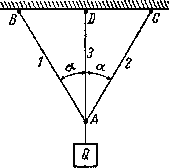
Рис.1. Расчетная схема однократно статически неопределимой стержневой системы.
Зададимся отношением площадей стержней; примем, что все три стержня будут иметь одинаковую площадь F. Получим:
1. 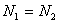
2. 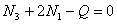
3. 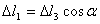
Используя закон Гука, получим:
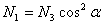
Следовательно:
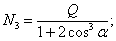
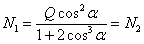 .
.
Диаграмма растяжения.Для изучения физико-механических свойств материала и установления значений предельных напряжений (предела пропорциональности, предела упругости, предела текучести, предела прочности, и т.п.), необходимых для оценки прочности и деформативности материалов, проводят испытания образцов материала вплоть до разрушения. Они проводятся на специальных испытательных машинах, создающих постепенно возрастающую нагрузку на испытываемый образец. Основным видом исследования механических свойств материала является испытание на растяжение образцов, представляющих собой, как правило, стержни круглого сечения.
При испытании автоматически строится диаграмма растяжения или сжатия. Имея диаграмму испытания и пользуясь разработанными в сопротивлении материалов методами расчёта, можно прогнозировать поведение реальной конструкции, изготовленной из того же материала.
При нагружении снимаются показания величины растягивающей силы и длины образца. Затем строится условная диаграмма растяжения в координатах 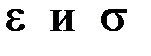 . Напряжение в сечении определяют по зависимости
. Напряжение в сечении определяют по зависимости 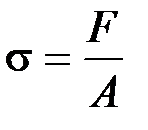 , где
, где 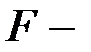 сила нагружения,
сила нагружения, 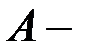 площадь поперечного сечения образца.
площадь поперечного сечения образца.
Относительная линейная деформация определяется из выражения
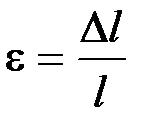 , где
, где 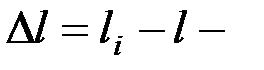 относительное удлинение образца;
относительное удлинение образца;
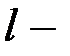 исходная длина образца;
исходная длина образца;
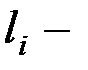 длина образца в данный момент отсчета.
длина образца в данный момент отсчета.
На диаграмме растяжения можно выделить четыре характерные участка (рис.2).
Участок 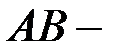 участок пропорциональности. На этом участке выполняется закон Гука. На участке
участок пропорциональности. На этом участке выполняется закон Гука. На участке 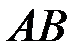 - упругие деформации, т.е. после снятия нагрузки образец будет иметь первоначальные размеры.
- упругие деформации, т.е. после снятия нагрузки образец будет иметь первоначальные размеры.
Участок 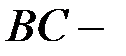 площадка текучести. На этом участке происходит удлинение образца без изменения нагрузки. Напряжение, при котором происходит течение образца, называется пределом текучести и обозначается
площадка текучести. На этом участке происходит удлинение образца без изменения нагрузки. Напряжение, при котором происходит течение образца, называется пределом текучести и обозначается 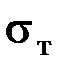 .
.
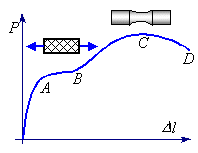


Рис. 2
В точке 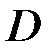 происходит образование шейки и на участке
происходит образование шейки и на участке 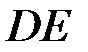 происходит местное удлинение образца. Напряжение, при котором образуется шейка, называется пределом прочности и обозначается
происходит местное удлинение образца. Напряжение, при котором образуется шейка, называется пределом прочности и обозначается 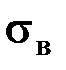 .
.
Для деталей, изготовленных из пластичных материалов, действующие напряжения не должны превышать напряжения текучести 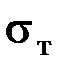 . С этой целью вводят понятия допускаемых напряжений, которые рассчитываются по зависимости:
. С этой целью вводят понятия допускаемых напряжений, которые рассчитываются по зависимости: 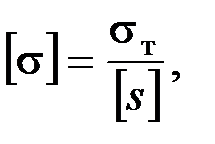 где
где 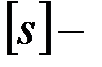 допускаемый коэффициент запаса прочности, который зависит от назначения детали, точности расчетных формул и некоторых других факторов.
допускаемый коэффициент запаса прочности, который зависит от назначения детали, точности расчетных формул и некоторых других факторов.
Условия прочности и жесткости конструкции. В сопротивлении материалов определяются наибольшие напряжения в элементах сооружений или деталях машин. Они сравниваются с нормативными величинами, т. е. с напряжениями, которые можно допустить, не опасаясь повреждения или разрушения этих элементов (деталей). Проверке подлежат также деформации тела и перемещения его отдельных точек. Прочность конструкции будет обеспечена, если максимальное напряжение в ней не будет превышать допускаемого напряжения
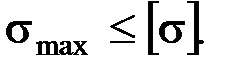 .
.
Для бруса, испытывающего напряжения растяжения, условие прочности будет иметь вид: 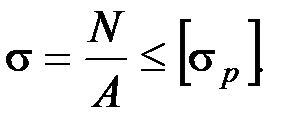
Условие жесткости при растяжении бруса определяется зависимостью
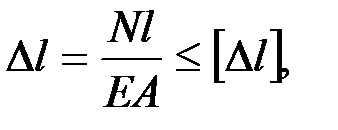 где
где 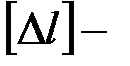 допустимая деформация бруса.
допустимая деформация бруса.
