Максиминная и минимаксная стратегия

Если функция выигрышей является выпуклой, то такая игра называется выпуклой. Для них разработаны приемлемые методы решения, состоящие в отыскании чистой оптимальной стратегии (определённого числа) для одного игрока и вероятностей применения чистых оптимальных стратегий другого игрока. Такая задача решается сравнительно легко.Как было отмечено, каждый игрок стремится обеспечить себе максимально возможный выигрыш при любых действиях противника. Поэтому рассмотрим следующий вопрос: как должны вести себя игроки в матричной игре, чтобы получить больший выигрыш, т. е. в чем состоит оптимальность в матричной игре?

Пусть игрок I выбрал стратегию 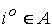, тогда игрок II выберет такую стратегию 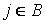, которая максимизирует его выигрыш и тем самым минимизирует выигрыш его противника. Стратегия игрока I, обеспечивающая ему наибольший выигрыш из всех возможных, независимо от действий противника, будет состоять в выборе такого 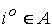, для которого минимальный выигрыш будет наибольшим, т. е.

.

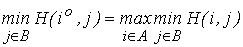Величину

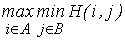(17.3)

принято обозначать через 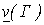(или просто v) и называть нижним значением (нижней ценой) игры, а соответствующую этому значению стратегию i° игрока I — максиминной стратегией. Если игрок I придерживается данной стратегии, то его выигрыш будет не меньше максиминного значения, то есть

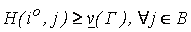(17.4)

Аналогично стратегия j°, определяемая равенством

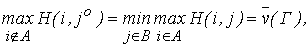
называется минимаксной стратегией игрока II, а соответствующее значение 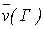(или просто 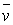) — верхним значением (верхней ценой) игры.

Если игрок II придерживается данной стратегии, то его проигрыш будет не больше минимаксного значения, т. е.

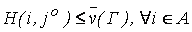(17.5)

Полагая, что в неравенстве (17.4) j = j°, а в выражении (17.5) i = i°, получим:

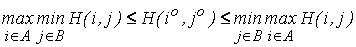(17.6)

Принцип, которого придерживается игрок I, называется принципом максимина, так как его гарантированный выигрыш равен величине (17.3). Игрок II также придерживается этого принципа, так как

.

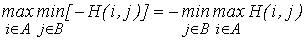Из неравенства (17.6) следует, что во всякой матричной игре 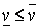.При этом возможны два следующих случая:

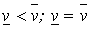. (17.7)

В первом случае игрок I может обеспечить себе выигрыш 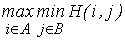, игрок II в состоянии ему не дать больше, чем .

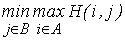Вопрос о разделе между игроками разности 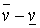(а в рассматриваемом случае она положительна) остается, таким образом, открытым. Это влечет за собой неопределенность в действиях игроков. Поясним сказанное.

Пример.

.

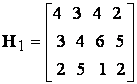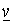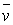Нахождение и матрицы Н может быть проведено по следующей схеме:

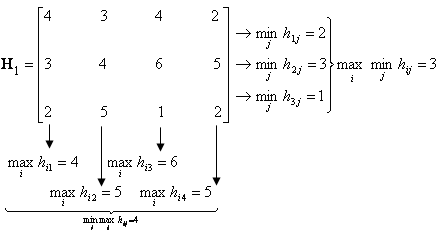
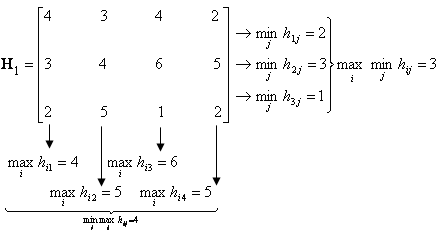
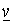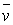= 3, = 4, 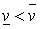; 2-я строка — максиминная стратегия; 1-й столбец - минимаксная стратегия. Применение максиминной и минимаксной стратегий приводит к выигрышу игрока I, равному 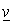(разность 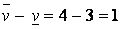достается игроку II, но можно привести пример, когда эта разность достается игроку I). Однако игрок I в игре 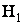, отклоняясь от максиминной и выбирая первую стратегию, может выиграть 4>3 (при условии, что игрок II придерживается минимаксной стратегии). Но игрок II, разгадав намерения игрока I, может выбрать свою четвертую стратегию и тем самым наказать его (даст ему 2<3). Игрок I в свою очередь может изменить решение и выбрать такую стратегию, при которой будет наказан игрок II, и т. д. И это будет происходить во всех играх, в которых .

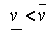Итак, при 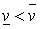максиминная и минимаксная стратегии не являются оптимальными.

Рассмотрим теперь второй случай. Равенство (17.7) означает, что величина, которую гарантирует себе игрок I, совпадает с величиной, больше которой игрок II не позволит ему получить. Поэтому игрокам необходимо выбрать максиминную и минимаксную стратегии соответственно.

Пример.

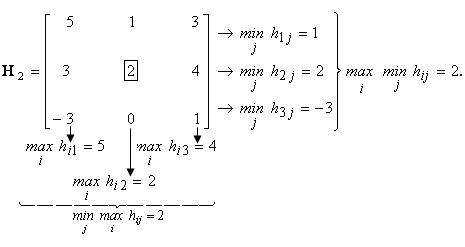
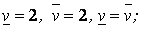2-я строка — максиминная стратегия; 2-й столбец — минимаксная стратегия. В этом случае любое отклонение каждого из игроков от этих стратегий (игрока I — от максиминной, игрока II — от минимаксной) не может оказаться выгодным.

В случае 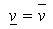максиминная и минимаксная стратегии называются оптимальными стратегиями игроков, а общее значение 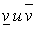(в дальнейшем мы его будем обозначать через v) — значениемили ценой игры.

Оптимальные стратегии будем обозначать через i*, j*. Нужно установить связь между принципом максимина и седловой точкой функции H(i, j). Вспомним определение седловой точки.

Точка (а, b) называется седловой точкой функции Н, если

.

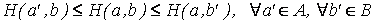Это неравенство выражает следующее свойство функции Н в точке (а, b): при любом изменении значения переменной а значение функции Н может уменьшиться, а при изменении значения переменной b — увеличиться. Термин “седловая точка” вводится по аналогии с термином “поверхность седла”, которая искривляется вверх в одном направлении и вниз — в другом.