Вопрос 25 Функциональные посл-ти и ряды. Осн. опр. Равномерная сх-ть ф-ции и рядов. Признак Вейерштрасса. Непрерывность, почленная дифференцируемость и интегрируемость функц. рядов.

Пусть на множестве Х задана последовательность функций 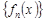, n=1,2… Пос-ть наз. ограниченной, если сущ. такое число С>0, что для всех n и всех 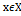|f_n(x)|<C, a пос-ть ф-ции наз. сходящ. на множестве Х, если при любом фиксир. 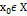сходится числ. пос-ть .

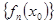Если пос-ть 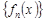сх-ся на множестве Х, то ф-ция f(x) определяемая при каждом 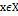равенством 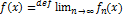, называется пределом функц. пос-ти. Множество всех числ. рядов 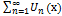в каждом из которых 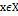произв. фиксирована наз. функциональным рядом, а 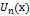- члены функц. ряда.

Сумма 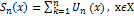- част. сумма функц. ряда, а 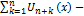его n-ым остатком.

Ряд 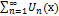наз. сх-ся, если сход-ся функциональ. п-ть его частичн. сумм 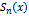при этом 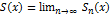наз суммой этого функц. ряда. Если при любом фиксир. 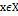сх-ся абсолютно, то ряд абсолютно сходится.

Признаки равномерной сходимости

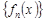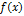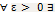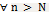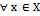Функц. пос-ть назыв. равном. сх-ся к ф-ции на мн-ве Х, если номер N: и выполн. нер-во 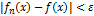. При этом пишут .

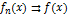Теорема : Для того, чтобы пос-ть 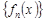равном. сх-сь к f(x) на мн-ве X необходимо и достаточно, чтобы

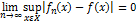
Признак Вейерштрасса

Если числ. ряд 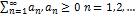сх-ся и для всех 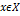и всех n, n=1,2,… выполн. нер-во 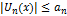, то ряд сх-ся абсолютно и равномерно.

Док-во: Абсолютн сх-ть функц. ряда при каждом фиксир. x из множ-ва X следует из признака сравнения. Докажем равном. сх-ть.

Зафиксируем произвольн. 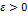. В силу сх-ти ряда 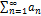для этого 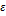найдется номер n_o: при n>n_o 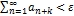. Для всех n и для всех 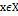для остатков функц. ряда имеем 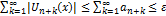. Значит, остатки ряда сх-ся равномерно 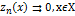. Значит и сам ряд сх-ся равномерно.

Вопрос 23 Числовые ряды, осн. определения, св-ва сходящихся рядов, критерий Коши сх-сти ряда, Признаки сх-ти числ. рядов с неотрицательными членами: Интегральный, сравнения, Даламбера, Коши, Теорема о перестановке членов ряда.

ОПР: Пара последовательносте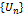й и 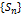, где S_n=U₁+U₂+…+U_n называется числ. рядом или бесконечной суммой и обознач. 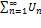. 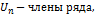а эл-ты пос-ти S_n-частичные суммы ряда. Если сущ. конечный предел 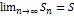, то ряд – сходящийся и 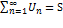. Если пос-ть не стремится к 0, то ряд расходится.

Простейшие свойства:

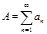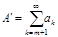1. Ряды и либо оба сходятся, либо оба расходятся. (Очевидно, т.к. критерий Коши даёт для обоих рядов одно и то же неравенство. При этом если ряды сходятся, то 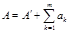) и 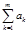- n-ый остаток ряда.

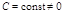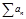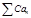2. Пусть . Тогда и либо оба сходятся, либо оба расходятся. (Если обозначить 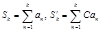, то ясно, что 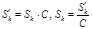. Отсюда, если 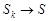, то 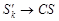и т.п.).

3. Есл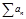и и 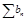оба сходятся, то при 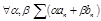тоже сходится, причём .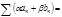

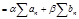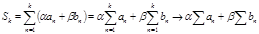
(при ).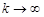

Критерий Коши сх-сти ряда

Для того чтобы ряд сх-ся необх. и дост, чтобы для 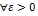нашлось бы число n_ε, такое, что для всех n> n_ε и целых p.

Док-во: 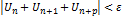. Это утвержд. непосредств.=> из критерия Коши из последней сход-ти, поскольку +

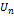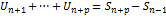
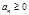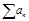Необходимый и достаточный признак сходимости: Если , то сходится тогда и только тогда, когда 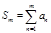ограничена (сверху). То, что ряд сходится, равносильно тому, что существует конечный 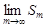, а это, т.к. 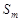не убывает, равносильно ограниченности сверху .

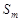Ряды с положительными членами

Если 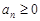, то 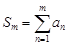не убывает. (Действительно, 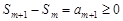для 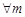, т.е. ).

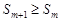Признак сравнения: Пусть даны 2 ряда 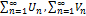и 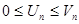. Тогда из сходимости 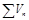следует сходимость 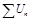, из расходимости 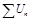следует расходимость .

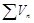Док-во: а) Если ряд 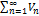сх-ся, то он имеет конечн. сумму σ. Тогда 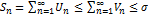. Пос-ть частичн. сумм 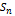огранич. сверху, значит в силу леммы ряд 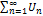сх-ся.

б) Если ряд 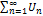расх-ся, то и и ряд 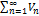расх-ся, т.к. если это было не так и ряд 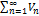сх-ся, тов силу пункта а) 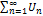сх-ся.

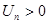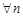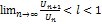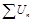Признак Даламбера: Пусть . Если при , начиная с некоторого, будет , то сходится, если же 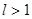, то 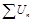расходится.

Док-во: Пусть l<1. Выберем число q так, что l<q<1. Т.к. 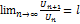, то найд. номер n_o, что при n>n_o выполн. нер-во 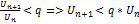. Применим это нер-во последно для n=n_о+1,n_о+2…Получим 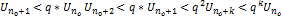. Просуммируем эти нер-ва: 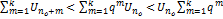. Устремим 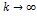. Ряд 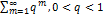представл. собой сумму членов бескон. убыв. геометр. прогрессии. Значит в силу признака сравнения сх-ся и остаток ряда 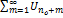, а значит и сам ряд сх-ся.

Радикальный признак Коши: Если для ряда 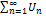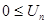, =1,2… существует 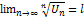, то при l < 1 ряд сх-ся, при l > 1 рас-ся.

Док-во: Пусть l<1, тогда из существ 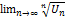для : l<q<1 найдётся номер n_o: ∀ n_о выполн. нер-во 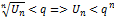, n=n_о+1,n_о+2… Т.к. ряд 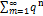сх-ся, как бескон. убыв. геометр. прогрессия, то остаток ряда 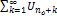, а значит и сам ряд сх-ся.

При 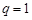как в признаке Даламбера, так и в признаке Коши требуется дополнительное исследование.

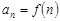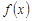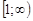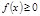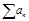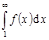Интегральный признак Коши-Маклорена: Пусть , причём непрерывна на , монотонно убывает и . Тогда и либо оба сходятся, либо оба расходятся.

Док-во: Пусть k≤x≤k+1, k=1,2… Т.к. f(x) убывает, то f(k)≥f(x)≥f(k+1). Проинтегрируем от k до k+1:

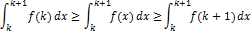
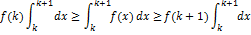
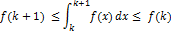
Проинтегрируем эти нерва от 1 до n: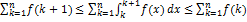

Замечание: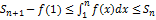

Если ряд сх-ся и его сумма равна S, то мнжво интегралов 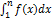ограничено сверху, а в силу неотрицат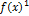 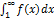сх-ся.

Теорема о перестановке членов ряда.

Пусть ряд 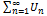с неотр. членами сх-ся и имеет сумму S, тогда новый ряд, полученный в рез-те перестановки членов исходн. ряда так же сх-ся и имеет ту же сумму.

Док-во: Пусть ря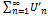д , а его частичн. сумма. Слагаемые этой частичн. суммы входят в исх. ряд под номерами k₁, k₂,…k_n. Обозначим N – наиб. из этих номеров, тогда пусть S_N –частич. сумма исх. ряда. Тогда 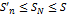. Т.к n произвольна и S’_n возрастает и огранич. сверху, то новый ряд сх-ся и его сумма 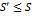. Предполагаем аналог. рассуждения, взяв за исход. ряд не 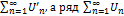. тогда получим 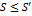, значит .

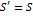Вопрос 26 Степенные ряды. Радиус сх-ти и круг сх-ти, формулы Коши-Адамара и Даламбера для вычисления радиуса сх-ти. Почленнаядиф-ть и инт-ть степ.рядов. Ряды Тейлора, теорема о разложимости, степ.ряды элементарных ф-ций.

Степенными рядами называются ряды вида 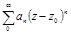или 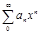.Формула Коши-Адамара: Для любого степенного ряда 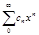существует число 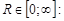при 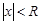ряд сходится абсолютно, при 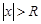ряд расходится. Если R = 0, то ряд сходится только при x= 0. Если R = ¥, то ряд абсолютно расходится для "x. Это число R называется радиусом сходимости и может быть найдено по формул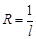е: , где 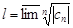Док-во:Пусть RÎ (0;¥), т.е. lÎ (0;¥). а) Возьмём сначала 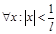, т.е. 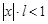. Тогда существует достаточно малое 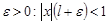. По определению 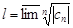правее l + e может быть только конечное число 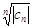, т.е. $N:для "n>N будет 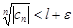. Тогда для 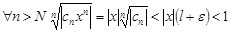, откуда по радикальному признаку Коши 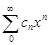сходится абсолютно для 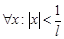.б) Возьмём теперь 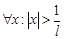, т.е. 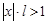. Тогда существует достаточно малое 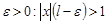. По определению 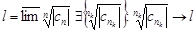. Тогда $K: для "k>K будет 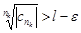, значит 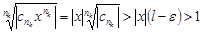, откуда при 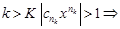ряд расходится, т.к. 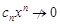при n®¥.Пусть теперь R = ¥, т.е. l = 0, т.е. 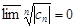. Т.к. 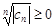для "n, то все частичные пределы последовательности 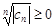, а т.к. наибольший из них равен 0, то у 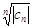один частичный предел, т.е. 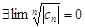. Покажем, что для 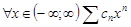абсолютно сходится. Т.к. 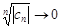при n®¥, то $N: для "n>N будет 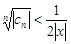. Тогда 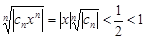и по радикальному признаку Коши 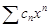сходится абсолютно.Пусть, наконец, R = 0, т.е. l = ¥. Это значит, что 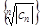не ограничена сверху. 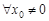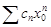Докажем, что для ряд расходится. Предположим, что он сходится. Тогда 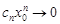при n® 0. Тогда 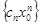ограничена, т.е. 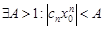, откуд 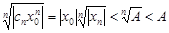, а, значит, 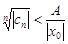, т.е. 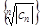ограничена, что противоречит условию, следовательно, 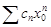расходится.Для 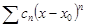будет абсолютная сходимость при 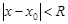и расходимость при 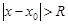.Множество 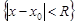будем называть кругом сходимости.

Различие между сходимостью и абсолютной сходимость у 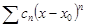может быть только при 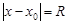.На окружности 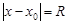(в комплексной плоскости) возможны разные случаи.Пусть для 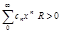. Тогда в 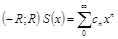– непрерывная функция.Возьмём 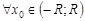. Тогд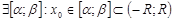а . На 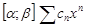сходится равномерно. Все его члены 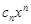непрерывны, следовательно, 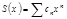непрерывна на 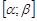, в том числе в точке 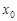. Т.к. эта точка – любая из 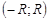, то 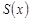непрерывна на .

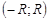Диф и интегр. R сход степ ряда и а₀+а₁х+3а₂х²+…ряда получ из него формальн диф-ния свпадает а₁+2а₂х+3а₂х²+…Док-во: Пусть R сход степ ряда 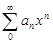=R,R сход 2-го ряда=R₁:

2.Степ ряд 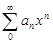диф-ют в пределах открытого круга 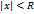сх-ти 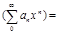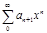Т.К степ ряд сход на [-q;q], наход строго внутри и нтерв сход-ти, то степ ряд можно почленно 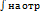[x.x₀]справ-ва ф-ла 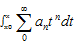= 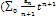)|^x_x0=a₀(x-x₀)- 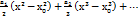х₀,х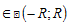

Ряд Тейлора.f(x) разлагатся в степ ряд, если найдутся такие числа а_n, n=0123..., что f(x)= 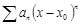Теорема.Чтобыf(x) разлогалась в степ ряд, на инт-ле (x₀-R,x_0+R)необх и дост, чтобы она была в этом инт-ле и ост член в ф-ле Тейл к→0 при n→∞

Разложения в ряд Тейлора: