Составление и линеаризация дифференциальных уравнений САУ

Процессы, происходящие в САУ, в общем случае описываются нелинейными дифференциальными уравнениями, которые могут быть решены лишь в отдельных редких случаях. Однако для достаточно большого числа систем эти уравнения с приемлемой для решения практических задач точностью могут быть заменены линеаризованными.

Рассмотрим принцип линеаризации на примере системы, у которой входной и выходной сигналы связаны нелинейной статической зависимостью . Пусть в установившемся режиме величина входного сигнала равна и его отклонения от этого значения в переходных процессах достаточно малы.

Разложив нелинейную зависимость в ряд Тейлора в окружности точки установившегося режима и, отбросив члены ряда выше первого порядка малости, получим следующую приближенную зависимость:

, (2.1)

где 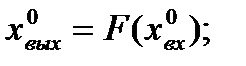- значение производной функции по 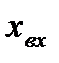при подстановке в выражение этой производной значения = .

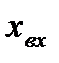Рис. 2.1. Линеаризация статической нелинейности

Выражение (2.1) можно переписать в виде:

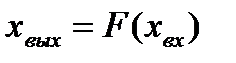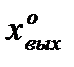, (2.2)

где ; ;

.

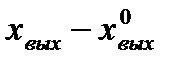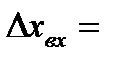
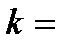
Проведенная линеаризация имеет простую графическую интерпретацию: она соответствует (рис. 2.1) замене действительной нелинейной характеристики касательной к ней в точке, соответствующей установившемуся режиму. Коэффициент k в выражении (2.2) равен тангенсу угла наклона этой касательной относительно оси 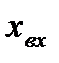. Поэтому его величина может быть найдена простым графическим построением без нахождения аналитического выражения нелинейной зависимости и ее производной.

В более общем случае, система описывается нелинейным дифференциальным уравнением, связывающим производные по времени входного и выходного сигналов:

.

(2.3)

Разложив нелинейную функцию (2.3) в ряд Тейлора в точке установившегося движения, получим следующее линейное дифференциальное уравнение для приращения переменных:

….+ …

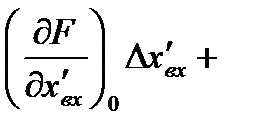
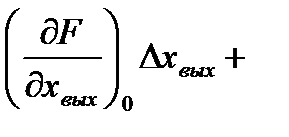
+…… ….. , (2.4)

где 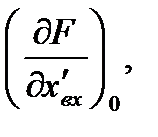.., и т.д. – значения производных функции (2.3) полученные при подстановке значений входного и выходного сигналов, соответствующих установившемуся режиму.

Следовательно, процедура линеаризации нелинейных систем дает возможность описать их линейными дифференциальными уравнениями в отклонениях. Очевидно, что допустимость такой линеаризации ограничена требованием к незначительности отклонений сигналов от их установившихся значений. Кроме того, поскольку такая линеаризация основана на разложении в ряд Тейлора, она применима только к непрерывно дифференцируемым нелинейностям.

Нелинейные звенья и системы, не удовлетворяющие этому требованию, называются существенно нелинейными. К существенно нелинейным звеньям относятся звенья с прерывистыми характеристиками, например, звенья с релейными характеристиками или неоднозначными характеристиками типа петли гистерезиса.

2.2. Основные свойства преобразования Лапласа. Операторные уравнения САУ. Передаточные функции линейных звеньев и систем

В общем случае дифференциальное уравнение, связывающее изменение во времени входной и выходной сигналы линеаризованной системы, имеет следующий вид:

(2.5)

Решение дифференциальных уравнений (2.3) – (2.4) зачастую связа­но со значительными трудностями, а во многих случа­ях, например в следящих системах, не может быть осу­ществлено, так как неизвестно управляющее воздейст­вие. По этим причинам исследование систем ведется косвенными методами, например, базирующимися на операционном преобразовании Лапласа.

Приведем основные сведения о преобразовании Лапласа, которые будут использованы при рассмотрении систем, описываемых линейными дифференциальными уравнениями.

Преобразованием Лапласаназывают интегральное преобразование:

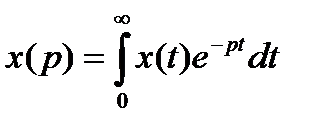, (2.6)

определяющее соответствие между функцией 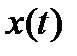вещественного переменного (в рассматриваемой теории – функцией времени 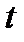) и функцией 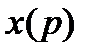комплексного переменного . При этом 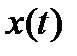называют оригиналом, а 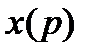– изображениемили изображением по Лапласу. Символическая запись такого преобразования:

= ,

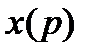где – оператор преобразования Лапласа.

Предполагается, что функция времени 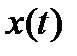, которая подвергается преобразованию Лапласа, обладает следующими свойствами:

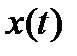· определена и дифференцируема на всей положительной числовой полуоси ;

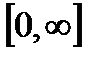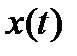· = 0 при ;

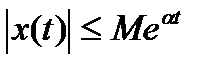· существуют такие числа М и , что при .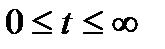

Функции, обладающие указанными тремя свойствами, часто называют функциями-оригиналами.

Соотношение

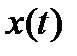= , (2.7)

определяющее по известному изображению его оригинал (в точках непрерывности последнего), называют обратным преобразованием Лапласа. В нем интеграл берется вдоль прямой Re p = 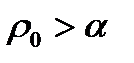. Символически обратное преобразование Лапласа можно записать так:

= ,

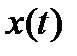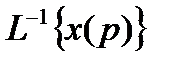где – символ обратного преобразования Лапласа.

Основные свойства (теоремы) преобразования Лапласа

1. Линейность преобразования. Для любых постоянных 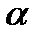и

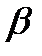
. (2.8)

2. Дифференцирование оригинала. Если производная 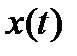является функцией-оригиналом, т.е. обладает указанными тремя свойствами, то 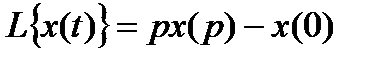, где 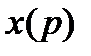= 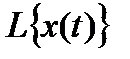, 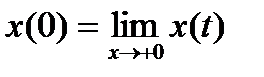. И вообще, если n-я производная 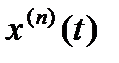является функцией-оригиналом, то

,

где 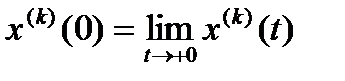, k=0,1,…n-1.

Если начальные условия нулевые, т.е. , то последняя формула принимает вид:

. (2.9)

Таким образом, при нулевых начальных условиях дифференцированию соответствует умножение изображения на р.

3. Интегрирование интеграла. Интегрирование оригинала сводится к делению изображения на р:

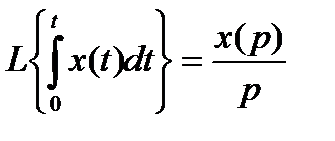. (2.10)

4. Теорема запаздывания. Для любого положительного числа

. (2.11)

5. Теорема умножения изображения. Если и – оригиналы, и – их изображения, то

. (2.12)

Интеграл правой части равенства называют сверткой функций и и обозначают:

= .

6. Теоремы о предельных значениях. Если 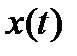– оригинал, а 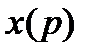– его изображение, то

, (2.13)

и при существовании предела

. (2.14)

7. Теорема разложения. Если изображение сигнала представляет собой дробно-рациональное выражение, т.е.

,

причем степень полинома числителя меньше степени полинома знаменателя и все n корнейуравнения простые, то для нахождения оригинала, соответствующего изображению 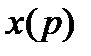, может быть использована формула (формула разложения):

(2.15)

где 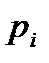- корень уравнения , .

В таблице 2.1 приведены выражения изображения Лапласа для некоторых типовых сигналов.

Таблица 2.1

Изображения по Ла­пласу типовых сигналов

Оригинал	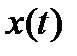Изображение	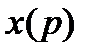Оригинал	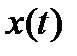Изображение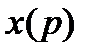
δ(t)
1(t)		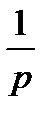sin( )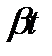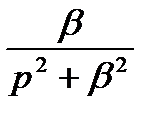
		cos( )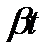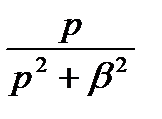

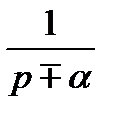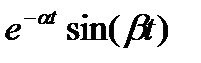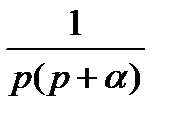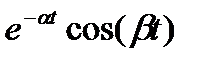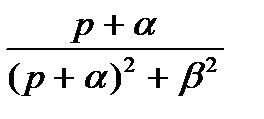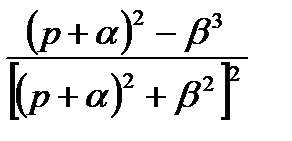Применяя преобразование Лапласа к дифференциальному уравнению (2.5) и считая начальные условия нулевыми, получим следующее операторное уравнение, связывающее изображения входного 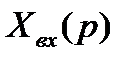и выходного 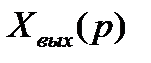сигналов системы:

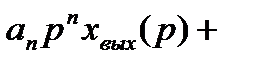
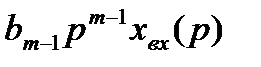..+ + +..+ (2.16)

или

,

где А(p) = 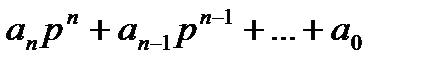; В(р)= .

Введем в рассмотрение передаточную функ­цию звена (или системы) равную отношению изображения по Ла­пласу выходного сигнала к изображению по Лапласу входного сигнала при нулевых начальных условиях:

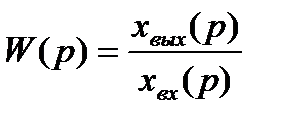. (2.17)

Из выражений (2.16) – (2.17) следует, что 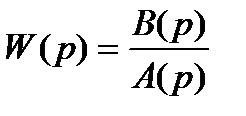и

. (2.18)

Выражение (рис. 2.18) связывает изображение выходного сиг­нала системы с изображением входного сигнала. Передаточная функция W(p) характеризует динамические свойства САУ, она не зависит от входного сигнала и полностью определяется коэффициентам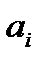и и , а те, в свою очередь, – параметрами и структурой системы.

Передаточная функция является дроб­но рациональной функцией относительно оператора пре­образования Лапласа:

. (2.19)

Рис. 2.2. Расположение нулей и полюсов передаточной функции САУ на комплексной плоскости

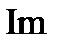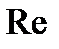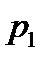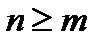Степень полинома знаменателя передаточной функции определяет порядок системы. В реальных системах степень полинома числителя передаточной функции не пре­вышает степени полинома зна­менателя: . Это условие называ­ют физической реализуемостьюСАУ; оно означает, что нельзя создать систему, пе­редаточная функция которой не удовлетворяла бы этому условию.

Корни полинома числителя передаточной функции (2.19) назы­вают нулями, а корни полино­ма знаменателя – полюсами САУ. При анализе САУ нули и полюсы (особенности передаточной функ­ции) удобно изображать точками на плоскости комплекс­ного переменного 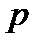(рис. 2.2). Так как коэффициенты передаточной функции – действительные числа, то нули и полюсы могут быть только вещественными ( ) либо комплексно-сопряженными ( и 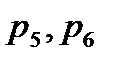) величинами. Если передаточная функ­ция звена или системы не содержит особенностей в правой части плоскости 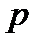, то систему называют минимально-фазовой, в противном случае ее считают неминимально-фазовой.

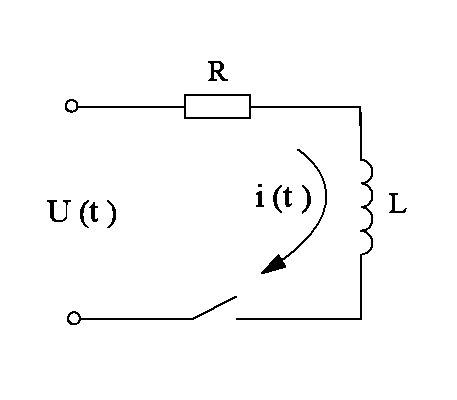
Рис.2.3 RC-цепочка

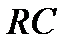Рассмотрим вопросы практического использования материала, изложенного в предыдущих параграфах, применительно к несложному объекту, взятому из электротехники - -цепочке (рис. 2.3). Входным сигналом такого объекта является приложенное к цепи напряжение 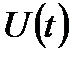, а выходным сигналом – ток в цепи 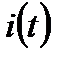. Несмотря на предельную простоту рассматриваемого объекта, на его примере можно проиллюстрировать некоторые вопросу, связанные с классификацией САУ. Очевидно, что это непрерывная система, построенная по принципу разомкнутого управления. Кроме того, полагая, что значения активного сопротивления и емкости неизменны, этот объект управления можно отнести к линейным и стационарным. Если приложенное напряжение незменно ( 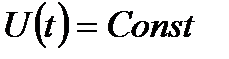), то, с точки зрения теории управления, рассматриваемая электрическая цепь – это система стабилизации, а если напряжение изменяется по определенному закону, например, синусоидальному, то это система программного управления.

Согласно второму уравнению Кирхгофа, дифференциалье уравнение, описывающие рассматриваемую 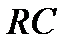- цепочку, имеет следующий вид:

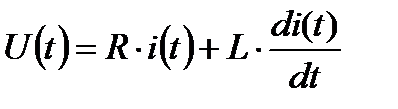
На основании (2.8) и (2.9) в результате выполнения преобразование Лапласа над обеими частями этого уравнения получим следующее операторное уравнение, связывающее изображения входного 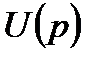и выходного сигналов объекта:

.

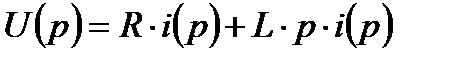Используя определение передаточной функции (2.17), получаем:

,

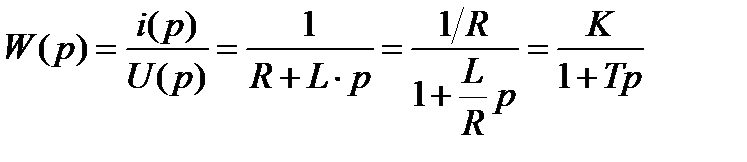где 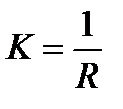– коэффициент усиления, а – постоянная времени объекта, с. Полученная передаточная функция соответствует одному из так называемых типовых звеньев – апериодическому звену первого порядка. Нулей такая передаточная функция не имеет, а для расчета ее полюсов необходимо, записать характеристическое уравнение системы, приравняв к нулю полином знаменателя:

.

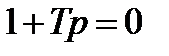Это алгебраическое уравнение первого порядка имеет единственный действительный корень – полюс передаточной функции:

.

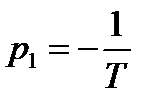2.3. Временные и частотные характеристики
звеньев и систем

Динамические свойства линейных звеньев и систем автоматического управления в целом могут быть описаны дифференциальными уравнениями и передаточными функциями, а также с помощью временныхи частотных характеристик. Временная характеристика представляет собой функцию времени, описывающую выходной сигнал звена (или системы) при подаче на вход звена определенного тестирующего сигнала. Частотные характеристики описывают установившиеся вынужденные колебания на выходе звена, вызванные гармоническим воздействием на входе.

Рис. 2.4. Единичное ступенчатое воздействие

Указанные характеристики могут быть сняты экспериментально или построены по уравнению звена. Имеется и обратная возможность – по экспериментально полученным характеристикам составить уравнение звена. Кроме того, с помощью этих характеристик можно определить реакцию звена на любое возмущение произвольного вида. Переходные и частотные характеристики однозначно связаны с дифференциальным уравнением звена и его передаточной функцией и наряду с ними являются исчерпывающим описанием динамических свойств звена.

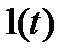К числу основных временных характеристик звена или системы относятся переходная функцияи функция веса.

Переходная функция звена представляет собой сигнал на выходе звена (реакцию звена), вызванный подачей на его вход единичного ступенчатого воздействия. Единичное ступенчатое воздействие(единичная ступенчатая функция, функция Хевисайда) – это воздействие, которое мгновенно возрастает от нуля до единицы и далее остается неизменным (рис. 2.4). Единичное ступенчатое воздействие обозначается и может быть описано следующим выражением:

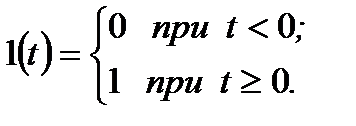(2.20)

Переходная функция обычно обозначается . Следовательно, – это выражение для при = .

Наряду с переходной функцией при описании звеньев и систем применяется функция веса, общепринятое обозначение которой 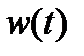. Эта временная характеристика представляет собой реакцию звена на дельта-функцию (единичную импульсную функцию, иглу Дирака). Дельта-функция, которая обозначается , – это математическая идеализация предельно короткого импульсного сигнала бесконечно большой амплитуды. Математически дельта-функцию можно описать следующим образом:

(2.21)

При этом согласно определению дельта-функции

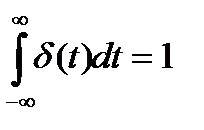.(2.22)

Таким образом, 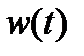- это при = .

Поскольку дельта-функция равна производной по времени от единичного ступенчатого воздействия, то и между переходной функцией, и функцией веса линейных звеньев существует аналогичная связь:

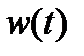
. (2.23)

И наоборот

.

Зная переходную и функцию веса, можно определить реакцию звена на произвольное входное воздействие при нулевых начальных условиях с помощью следующих формул:

; (2.24)

, (2.25)

где , – значения и 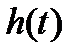при t = 0;

Выражения (2.24) и (2.25) легко получаются друг из друга, являясь вариантами интеграла Дюамеляили интеграла свертки. У реальных инерционных звеньев и систем h(0)=0, так как реакция на их выходе всегда отстает от входного воздействия. Поэтому в дальнейшем выражения (2.24) и (2.25) приводятся без первого слагаемого.

Временные характеристики могут быть выражены непосредственно через передаточную функцию звена с помощью преобразований Лапласа.

Поскольку ,в случае, когда входное воздействие 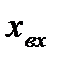(t) представляет собой единичный импульс , и с учетом того, что его изображение по Лапласу , получим следующее выражение для изображения функции веса звена:

w(p) =W(p) или , т.е.

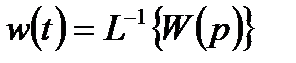. (2.26)

Таким образом, функция веса определяется через передаточную функцию по формуле обратного преобразования Лапласа, т.е. является ее оригиналом.

В случае, когда 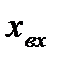(t) = 1(t), учитывая, что L = 1/p, получаем следующее выражение для изображения переходной характеристики:

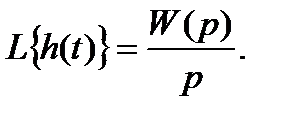
Следовательно, переходная характеристика звена равна:

При рассмотрении частотных характеристик считаем, что на входе системы дейст­вует гармонический сигнал с амплитудой и часто­той :

. (2.27)

По окончании переходного процесса на выходе линейной системы будут существовать гармонические колебания с той же частотой, что и у входного сигнала, но в общем случае отличающиеся от него по амплитуде и фазе, т.е. в установившемся режиме выходная величина звена равна:

, (2.28)

где – амплитуда установившихся выходных колебаний; 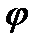– фазовый сдвиг между входными и выходными синусоидальными колебаниями.

При изменении частоты изменяется, как соотношение между амплитудами входных и выходных колебаний, так и фазовый сдвиг 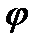между ними. При этом зависимость от частоты отношения амплитуд называется амплитудно-частотной характеристикой(АЧХ), т.е.

.

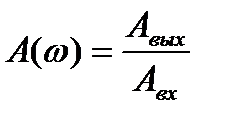Зависимость величины фазового сдвига от частоты называется фазо-частотной характеристикой (ФЧХ).

Определив амплитудно- и фазо-частотную характеристики системы, например, получив их экспериментально, можно построить еще одну частотную характеристику – амплитудно-фазовую(АФЧХ).

Амплитудно-фазовую характеристику, используя 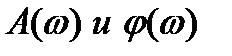в качестве полярных координат, строят на комплексной плоскости по следующим правилам. Задаются значением частоты ω_i, для которого по графику ФЧХ определяют величину фазового сдвига φ(ω_i) , а по графику АЧХ – величину A(ω_i).

Рис. 2.5. Примерный вид частотных характеристик инерционной САУ: а - амплитудно-частотной; б - фазо-частотной; в - амплитудно-фазовой

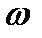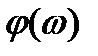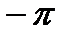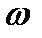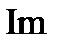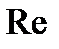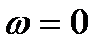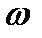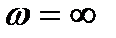а)

б)

в)

Из начала координат комплексной плоскости проводится луч под углом φ(ω_i) к положительной действительной полуоси. Угол откладывается против часовой стрелки, если φ(ω_i) > 0, т.е. когда выходной гармонический сигнал опережает входной, и в противоположном направлении, если φ(ω_i) < 0 .Из начала координат по этому лучу откладывается отрезок, длина которого в выбранном масштабе равна A(ω_i) (рис. 2.5, в).

Каждая точка амплитудно-фазовой частотной характеристики соответствует определенному значению частоты. Значения для конечного количества точек характеристики наносятся вдоль характеристики и указывают направление возрастания частоты ω.

Очевидно, что возможно и решение обратной задачи:по годографу амплитудно-фазовую частотную характеристику можно построить характеристики и . На рис. 2.5 приведен примерный вид этих характеристик для инерционной системы.

Как показано на этих рисунках, у таких звеньев в силу их инерционности амплитудная частотная характеристика по мере увеличения частоты в конце концов спадает до нуля. При этом, чем менее инерционно звено, тем шире его амплитудная частотная характеристика, т.е. тем больше полоса пропускаемых звеном частот, или просто его полоса пропускания.

Теоретически частотная характеристика продолжается до бесконечности, но практически полоса пропускания оценивается значением частоты, при котором отношение амплитуд окончательно становится меньше определенного, достаточно малого конечного значения. Это значение обычно берут равным 0,05 (на этой частоте амплитуда выходных колебаний падает до 5 % амплитуды входных колебаний). Наличие максимума у амплитудной частотной характеристики говорит о резонансных свойствах звена. Частота, соответствующая максимуму амплитудной характеристики, называется резонансной( ).

Фазовая характеристика у обычных инерционных звеньев (рис. 2.5, б) отрицательна ( (ω)< 0), т.е. выходные колебания отстают по фазе от входных, и это отставание растет с частотой.

Используя символическую форму записи гармонических сигналов x_вх(t) и x_вых(t), получим аналитические выражения для рассмотренных характеристик, их зависимость между собой и с передаточной функцией системы.

Символическая запись сигналов (2.27) и (2.28):

, .

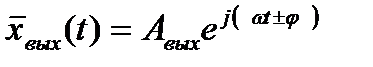Определим амплитудно-фазовую характеристику системы, как отношение выходного сигнала системы к входному, выраженное в комплексной форме:

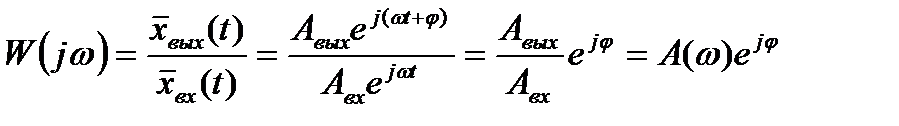. (2.29)

Из выражения (2.29) следует, что амплитудно-частотная и фазо-частотная характеристики является соответственно модулем и фазой (аргументом) амплидудно-фазовой характеристики:

A(ω) = |W(jω)| и φ(ω) = argW(jω).(2.30)

Очевидно, что на приведенных зависимостях между характеристиками основывалась рассмотренная методика построении W(jω) по A(ω) и φ(ω).

Комплексное выражение для W(jω) может быть представлено, как в форме (2.29), так и в виде:

W(jω) = P(ω) + jQ(ω), (2.31)

где P(ω), Q(ω) – соответственно вещественная и мнимая частотные характеристики системы.

Таким образом, получаем всего пять частотных характеристик: амплитудно-фазовую W(jω), амплитудно-частотную A(ω), фазо-частотную φ(ω), вещественную частотную P(ω) и мнимую частотную Q(ω). Между этими характеристиками, кроме зависимостей (2.30) – (2.31), имеются следующие очевидные связи:

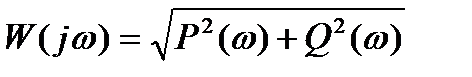; (2.32)

(2.33)

. (2.34)

Частотные характеристики системы не зависят от времени. В этом их принципиальное отличие от временных характеристик. Если временные характеристики определяют поведение системы в переходном процессе при различных типовых входных воздействиях, то частотные выражают зависимость параметров установившихся выходных синусоидальных колебаний от тех же параметров входных колебаний при различных частотах.

Частотные характеристики широко используются в инженерной практике при анализе и синтезе САУ. Особым их достоинством является то, что они могут быть получены экспериментальным путем, что особенно важно для систем, аналитические уравнения которых не представляется возможным получить из-за их сложности или малоизученности технологического процесса.

Несмотря на то, что частотные характеристики, например W(jω), отображают только установившиеся процессы в системе, они в полной мере определяет и ее динамические свойства.

Подставляя производные сигналов 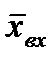(t) и равные

….

…. ,

в дифференциальное уравнение (2.5), получим:

[ ] =

= [ ] .

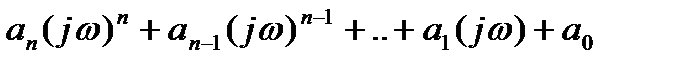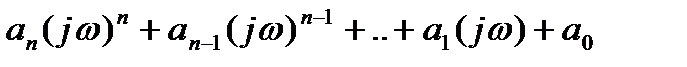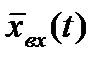Из полученного выражения определяем АФХ системы:

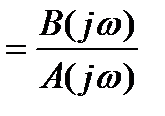. (2.35)

Сравнивая выражения (2.18) и (2.35) делаем заключение, что выражения для АФЧХ W(jω) системы может быть получено по ее передаточной функции W(p), в которой достаточно переменную p заменить на jω:

W( jω) = . (2.36)

Если в выражении (2.18) осуществить аналогичную замену p на jω, получим:

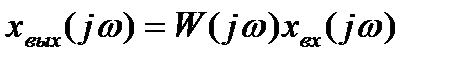, (2.37)

где и – и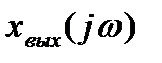зображения Фурье входного и выходного сигналов.

На основании выражения (2.37) амплитудно-фазовую частотную характеристику можно определить как отношение изображений Фурье выходного и входного сигналов системы при нулевых начальных условиях:

.

Выражению (2.26), связывающему с помощью преоб