Индуктивность при гармоническом воздействии
Пусть ток, протекающий по индуктивности, изменяется по гармоническому закону 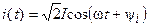 , где
, где 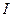 ,
, 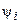 — действующее значение и начальная фаза тока.
— действующее значение и начальная фаза тока.
Используя связь между током и напряжением индуктивности, определяемую законом Фарадея, найдем мгновенное напряжение на индуктивности
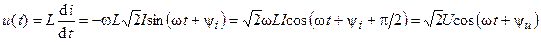 , (4.19)
, (4.19)
где 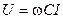 ,
, 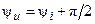 — действующее значение и начальная фаза напряжения на индуктивности.
— действующее значение и начальная фаза напряжения на индуктивности.
Из (4.19) видно, что напряжение на индуктивности изменяется по гармоническому закону, а его начальная фаза 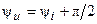 больше начальной фазы тока на
больше начальной фазы тока на 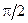 . Следовательно, напряжение на индуктивности опережает по фазе ток на 90°. Действующее значение напряжения на индуктивности пропорционально действующему значению тока, частоте и значению индуктивности.
. Следовательно, напряжение на индуктивности опережает по фазе ток на 90°. Действующее значение напряжения на индуктивности пропорционально действующему значению тока, частоте и значению индуктивности.
Определим мгновенную мощность индуктивности
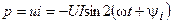 .
.
Мгновенная мощность индуктивности представляет собой гармоническую функцию с частотой  , которая аналогична мгновенной мощности емкости.
, которая аналогична мгновенной мощности емкости.
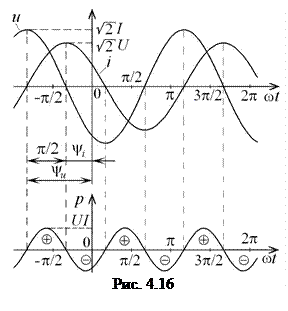 На рис. 4.16 изображены временные диаграммы напряжения, тока и мощности индуктивности. Когда ток и напряжение индуктивности одновременно положительны или отрицательны, имеет место положительный полупериод мощности, в течение которого индуктивность накапливает энергию магнитного поля. Когда ток и напряжение индуктивности имеют разные знаки, то имеет место отрицательный полупериод мощности, в течение которого индуктивность отдает энергию магнитного поля. В результате, среднее значение мощность за период равно нулю, что соответствует реактивному характеру сопротивления индуктивности.
На рис. 4.16 изображены временные диаграммы напряжения, тока и мощности индуктивности. Когда ток и напряжение индуктивности одновременно положительны или отрицательны, имеет место положительный полупериод мощности, в течение которого индуктивность накапливает энергию магнитного поля. Когда ток и напряжение индуктивности имеют разные знаки, то имеет место отрицательный полупериод мощности, в течение которого индуктивность отдает энергию магнитного поля. В результате, среднее значение мощность за период равно нулю, что соответствует реактивному характеру сопротивления индуктивности.
Заменим в (4.19) вещественные функции напряжения 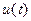 и тока
и тока 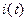 их изображениями в показательной форме записи
их изображениями в показательной форме записи 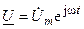 и
и 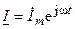 , получаем уравнение:
, получаем уравнение:
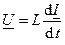 ;
;
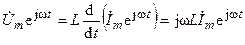 .
.
Сокращая оператор вращения 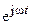 и учитывая, что
и учитывая, что 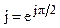 и
и 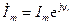 , найдём комплексную амплитуду напряжения
, найдём комплексную амплитуду напряжения
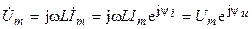 ,
,
где 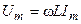 и
и 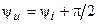 — модуль и начальная фаза комплексной амплитуды напряжения индуктивности.
— модуль и начальная фаза комплексной амплитуды напряжения индуктивности.
Поделив левую и правую части уравнения на 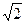 и учитывая, что
и учитывая, что 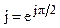 , находим комплексное действующее значение тока напряжения индуктивности
, находим комплексное действующее значение тока напряжения индуктивности
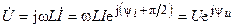 ,
,
где 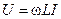 ,
, 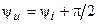 — модуль и аргумент комплексного действующее значение напряжения, которые совпадают с аналогичными значениями, найденными ранее путём преобразования вещественных функций.
— модуль и аргумент комплексного действующее значение напряжения, которые совпадают с аналогичными значениями, найденными ранее путём преобразования вещественных функций.
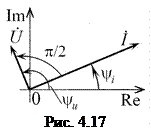
Векторная диаграмма комплексных тока и напряжения индуктивности показана на рис. 4.17. Вектор напряжения повернут относительно вектора тока на угол 90°против часовой стрелки, поскольку напряжение на индуктивности опережает по фазе ток на 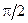 .
.
Найдем комплексное сопротивление индуктивности
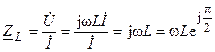
и комплексную проводимость индуктивности
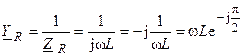 .
.
 и запишем их в показательной и алгебраической форме:
и запишем их в показательной и алгебраической форме:
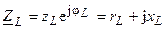 ,
, 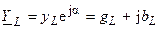 .
.
Определим модуль, аргумент, вещественную и мнимую части комплексного сопротивления:
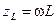 ,
, 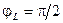 ;
;
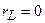 ,
, 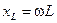 ,
,
и комплексной проводимости индуктивности:
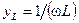 ;
;
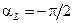 ,
, 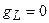 ,
, 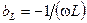 .
.
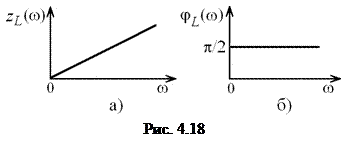
Модуль сопротивления индуктивности изменяется прямо пропорционально частоте, а аргумент является положительным и не зависит от частоты (рис. 4.18).
 На комплексной плоскости комплексные сопротивление
На комплексной плоскости комплексные сопротивление 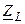 и проводимость
и проводимость 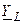 индуктивности изображаются векторами, ориентированными соответственно вдоль положительной и отрицательной мнимых полуосей (рис. 4.19 а, б). Комплексная схема замещения индуктивности в виде комплексного сопротивления показана на рис. 4.19,в.
индуктивности изображаются векторами, ориентированными соответственно вдоль положительной и отрицательной мнимых полуосей (рис. 4.19 а, б). Комплексная схема замещения индуктивности в виде комплексного сопротивления показана на рис. 4.19,в.
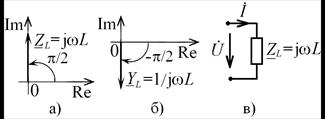
Рис. 4.19
Полученные выше соотношения показывают, что комплексные сопротивления и проводимости идеализированных реактивных элементов не зависят от амплитуды (действующего значения) и начальной фазы внешнего воздействия и определяются только параметрами этих элементов и частотой внешнего воздействия.
