Введение и постановка задач исследования
РЕФЕРАТ
Страниц __, рисунков __, источников __.
Ключевые слова: эмпирическое распределение случайной величины, начальные и центральные моменты, аппроксимирующее распределение, метод моментов, метод максимального правдоподобия, метод «вероятностной бумаги», критерии согласия.
Рассмотрены и исследованы задачи статистической обработки так называемых полных выборок в предположении их репрезентативности, то есть принадлежащих генеральной совокупности исследуемых объектов, с оценкой параметров альтернативных теоретических распределений, аппроксимирующих эмпирическую (ступенчатую) функцию распределения, двумя методами – методом моментов и методом максимального правдоподобия.
Разработано алгоритмическое и программное обеспечение для получения точечных оценок параметров двух практически важных распределений - распределения Вейбулла и гамма-распределения методом моментов и методом максимального правдоподобия. Разработан и программно реализован также алгоритм проверки выполнимости критерия А.Н. Колмогорова – критерия согласия аппроксимирующего распределения эмпирическому (ступенчатому) распределению.
Системы расчетов полностью реализованы в среде отечественного Программного комплекса «МВТУ 3.5».
Оглавление
ВВЕДЕНИЕ И ПОСТАНОВКА ЗАДАЧ ИССЛЕДОВАНИЯ.. 4
1. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ МЕТОДОВ МОМЕНТОВ И МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ.. 6
1.1. Оценка первых четырех выборочных начальных и центральных моментов и построение эмпирического распределения 6
1.2. Метод моментов. 9
1.3 Метод максимального правдоподобия (ММП) 10
1.4 О методе «вероятностной бумаги». 14
2. АЛГОРИТМЫ РАСЧЕТА ПАРАМЕТРОВ РАСПРЕДЕЛЕНИЙ МЕТОДОМ МОМЕНТОВ.. 15
2.1. Алгоритмы расчета параметров гамма-распределения методом моментов и его развитие. 15
2.2. Алгоритмы расчета параметров распределения Вейбулла. 16
3. АЛГОРИТМЫ РАСЧЕТА ПАРАМЕТРОВ РАСПРЕДЕЛЕНИЙ МЕТОДОМ МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ 18
3.1. Алгоритмы расчета параметров гамма-распределения. 18
3.2. Алгоритмы расчета параметров распределения Вейбулла для полной выборки. 21
3.3. Алгоритмы расчета параметров распределения Вейбулла для цензурированной выборки. 23
4 СТАТИСТИЧЕСКАЯ ПРОВЕРКА ГИПОТЕЗ. КРИТЕРИЙ «СТАРЕЮЩИХ» РАСПРЕДЕЛЕНИЙ.. 24
4.1 Критерий согласия А.Н. Колмогорова. 24
4.2 Критерии «стареющего» распределения. 26
5. ПРОГРАММЫ И РЕЗУЛЬТАТЫ РЕШЕНИЯ КОНКРЕТНОЙ ЗАДАЧИ ОБРАБОТКИ СТАТИСТИЧЕСКИХ ДАННЫХ 27
5.1. Постановка задачи. 27
5.2. Расчет первых четырех выборочных моментов и построение эмпирической функции распределения 28
5.3. Расчет параметров предполагаемых теоретических распределений методом моментов. 35
5.4. Расчет параметров предполагаемых теоретических распределениях методом максимального правдоподобия 50
5.5 Развитие метода максимального правдоподобия. 66
5.5 а. Метод вероятностной бумаги………………………………………………………………..
5.6 Сводка результатов, их анализ и выводы.. 70
Выводы. 76
ПРИЛОЖЕНИЕ 1 (справочное). 78
АЛГОРИТМЫ РАСЧЕТА ПАРАМЕТРОВ РАСПРЕДЕЛЕНИЙ МЕТОДОМ
МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ
3.1. Алгоритмы расчета параметров гамма-распределения
Для гамма-распределение с плотностью
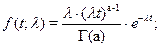
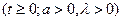
функция правдоподобия имеет вид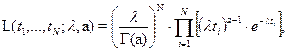 
где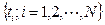 
— полная выборка наработок до отказа, 
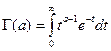— Эйлеров интеграл II рода.
Эквивалентная функция правдоподобия, после логарифмирования функции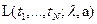 
, имеет вид
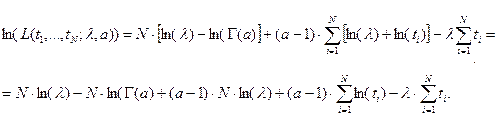
И в окончательном виде
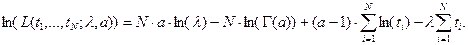
Необходимое условие экстремума:
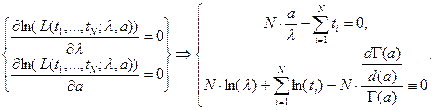
Последний член следует, напомним, из известной формулы для производной функции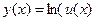 
, которая такова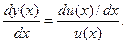 
Из первого уравнения следует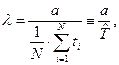 
где 
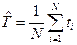- точечная оценка среднего времени наработки до отказа, рассчитанная по полной выборке.
Подставим теперь найденное выражение для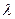 
во второе уравнение 
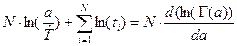
и преобразуем его к виду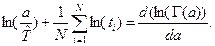 
(это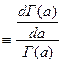 
).
Далее можно записать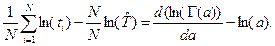 
Приводя левую часть уравнения к виду 
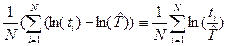, окончательно получим компактное уравнение для получения численной оценки параметра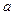 
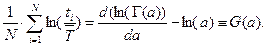
Или в более развернутом виде
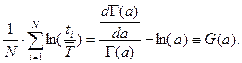
Получив оценку параметра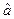 
, вычисляем и оценку параметра 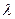по формуле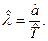 
Желательно получить в аналитическом виде и построить график функции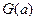 
. Есть несколько путей получения такой функции. Один из них — в использовании асимптотического разложения Джеймса Стирлинга для гамма-функции.
Асимптотическое разложение для гамма-функции таково
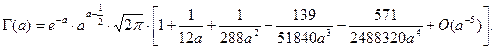
Здесь надо вывести выражение для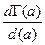 
и получить 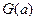в явном виде.
Заметим также, что (см. Справочник Корн и Корн по математик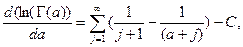е) 
где 
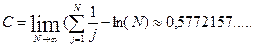е- постоянная Эйлера – Маклорена.
Прямой вычислительный алгоритм нахождения оценок 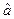и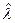 
для гамма-распределения приведем ниже. А здесь отметим, что умение использовать в расчетах именно гамма-распределение очень важно для практики, т.к. из гамма-распределения вытекают:
- Экспоненциальное распределение при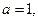 
- Распределение Эрланга при целом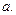 
( 
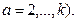
- Хи-квадрат распределение (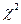 
- распределение) при 
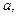кратном 
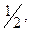и при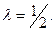 
Получим все необходимые соотношения и расчетные формулы
или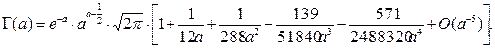 
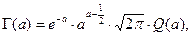
где
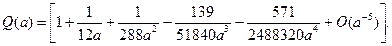
Далее
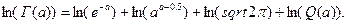
Заметим, что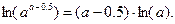 
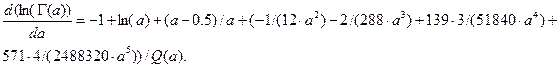
В итоге получим окончательно аналитическое выражение
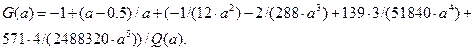
3.2. Алгоритмы расчета параметров распределения Вейбулла для полной выборки
Для этого распределения все характеристики представляются в аналитическом виде
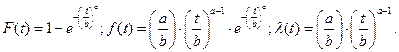
Функции правдоподобия:
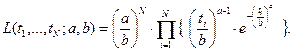
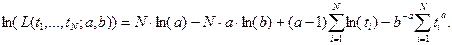
Необходимые условия экстремума:
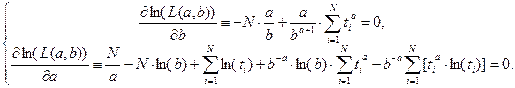
Из первого уравнения находим выражение для
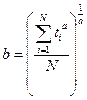
и, подставляя его во второе уравнение, приходим к уравнению:
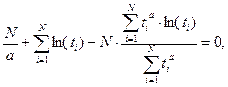
которое надо разрешить относительно параметра 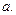При получении последнего уравнения использовано соотношение для коэффициента
.
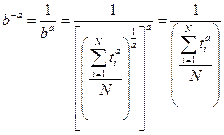С вычислительной точки зрения может быть целесообразнее принять следующую запись этого уравнения
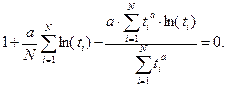
Для решения таких уравнений предлагается использовать идею непрерывного градиента и для нахождения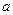 
решать следующее дифференциальное уравнение:
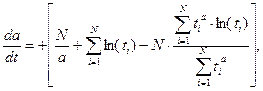
с начальным условием, например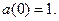 
Тогда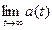 
даёт искомое значение оценки параметра 
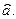После чего остается вычислить 
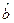по формуле 
.
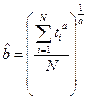3.3. Алгоритмы расчета параметров распределения Вейбулла для цензурированной выборки
Имеем усеченную выборку объемом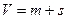 
, содержащую:
· ряд наработок с отказами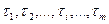 
;
· ряд безотказных наработок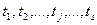 
.
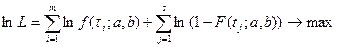
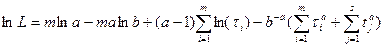
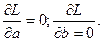
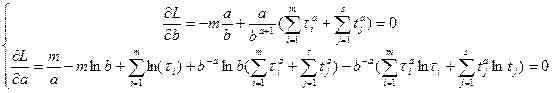
Из первого уравнения: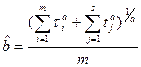 
.
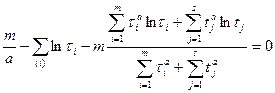
Решаем уравнение и находим параметр a.
Программа14
t=time;
{Расчет и оценка критерия "стареющего распределения }
M1=160.94; {т.е. M1=m1=T}
M2=161.1/2; {т.е. M2=m2/2!; m2=27945}
M3=161.26/6; {т.е. M3=m3/3!; m3=5031300;}
M4=160.3/24; {т.е. M4=m4/4!; m4=730570000}
Delt1=(M2^2-M1*M3);
Delt2=(M3^2-M2*M4);
Nerav1=sign(M2^2-M1*M3);
Nerav2=sign(M3^2-M2*M4);
output Nerav1,Nerav2,Delt1,Delt2;
Результат таков:
Оба неравенства выполнились. Правая часть каждого неравенства много больше левой части. Это говорит о том, что распределение стареющее. Таким образом, делаем окончательный вывод о принадлежности выборочного распределения распределению Вейбулла.
При выполнении настоящей работы отработаны вычислительные методы и в среде программного комплекса «МВТУ» разработано соответствующее алгоритмическое обеспечение. При этом обеспечивается решение сложных нелинейных алгебраических уравнений и полностью исключается применение таблиц.
Выводы
При выполнении работы развиты известные и предложены новые вычислительные процедуры и алгоритмы и разработано программное обеспечение информационных систем обработки статистической информации, получаемой из сферы эксплуатации, для решения задач объективной оценки характеристик и показателей надежности оборудования с использованием методов моментов, вероятностной бумаги и максимального правдоподобия для полных и цензурированных выборок без обращения к огромному числу таблиц. Эффективность предложенных алгоритмов проверена при решении конкретных задач. В работе сделан научно-технический задел для решения на ЭВМ перспективных задач обработки информации с малыми или ограниченными по объему выборками, в том числе с различными типами цензурирования, то есть усеченными выборками, методами моментов и максимального правдоподобия, как с точечными, так и интервальными оценками параметров предполагаемых распределений.
Список использованной литературы
1. Справочнике «Надежность технических систем» под ред И.А. Ушакова. – М.: «Радио и связь». 1985.
2. РД 50-690-89 «Методические указания. Надежность в технике. Методы оценки показателей надежности по экспериментальным данным». – М.: Изд-во стандартов, 1989.
3. Е.С. Вентцель. Теория вероятностей. – М.: Физматгиз, 1962
4. Г. Хан, С. Шапиро. Статистические модели в инженерных задачах: Пер. с англ. – М.: Изд-во «МИР», 1969.
5. Крамер. Математические методы статистики: Пер. с англ. – М.: Изд-во «МИР», 1975.
6. ГОСТ Р 50779.27-2007. Статистические методы. Критерии согласия и доверительные интервалы для распределения Вейбулла.
7. ГОСТ 11.008-75. Правила построения и применения вероятностных сеток.Приложение 1 (справочное)
Стандартные распределения и их свойства и характеристики
Гамма-распределение
Плотность вероятности наработки до отказа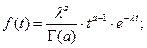 
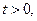
где 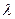— параметр масштаба ( 
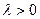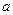), — параметр формы ( 
), 
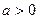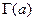— гамма-функция или эйлеров интеграл второго рода 
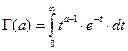или
.
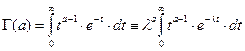Аналитического выражения для функции распределения наработки на отказ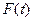 
не существует (аналитическое выражения для нее существует только для целых положительных значений параметра 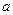; см. ниже распределение Эрланга).
Известны формулы связи моментов с параметрами "a" и "λ" гамма-распределения:
; 
; 
; 
; 
.
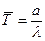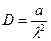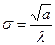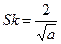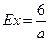Коэффициент вариации при этом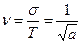 
. Мода: 
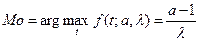для значений 
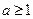. Квантиль 
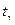находится из уравнения 
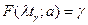для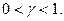 
Точка перегиба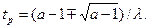 
Начальные моменты таковы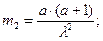 
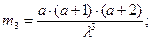
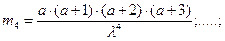
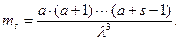
В задачах обработки статистических экспериментальных данных потребуются выражения и оценки численных значений производной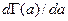 
и функции 
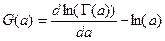или в развернутом виде 
.
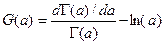Нетрудно показать, что =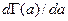 
,
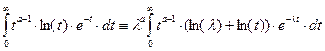а функция примет вид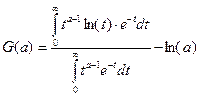 
.
При 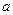— целом ( 
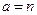) функция 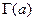принимает значения 
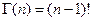, то есть,
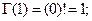
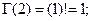
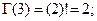
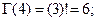
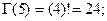... и т.д. Таким образом, гамма-функция Эйлера - это распространение функции или операции «факториал» на случай нецелых чисел, в том числе и отрицательных.
Табличные значения функции 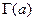в справочниках ограничены значениями аргумента "a", принадлежащими интервалу 
.
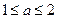Значения гамма-функции для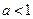 
, но при этом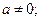 
... ,
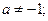
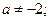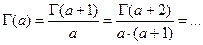При больших значениях a ( 
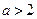) по формуле 
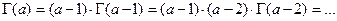, которые следуют из функционального уравнения Эйлера 
.
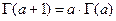Примеры:
; 
;
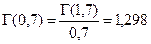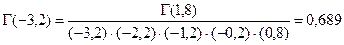Полезные соотношения и значения гамма-функции:
; 
.
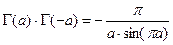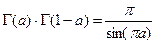Функция распределения времени наработки до отказа, как отмечалось выше, не имеет аналитического выражения. В общем виде она может быть представлена таким образом
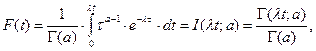
где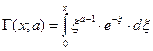 
— неполная гамма-функция.
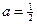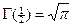при 
: 
; при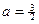 
: 
;
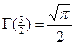Примечание. Из гамма-распределения «вытекают»:
при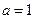 
— экспоненциальное распределение;
при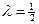 
и a, кратном 
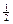, будем иметь χ2-распределение (при этом 
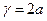— число степеней свободы);
при a — целом: a = 1; 2; ... ; k; ... — распределение Эрланга.
Существенное уменьшение вычислительных трудностей может быть достигнуто применением асимптотических разложений (аппроксимационных формул) Стирлинга:
.
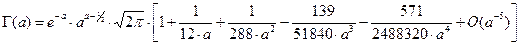Ряд Стирлинга полезен для больших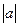 
. Для действительных положительных a абсолютные величины ошибки меньше, чем абсолютная величина последнего из взятых членов.
Другие полезные аппроксимации Стирлинга: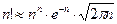 
при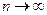 
.
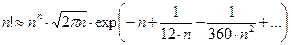. Известно важное неравенство:
< 
< 
.
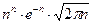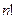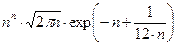Распределение Эрланга
Плотность распределения наработки до отказа:
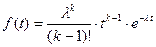
для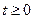 
; 
; 
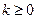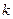— целое.
Функция распределения времени наработки до отказа:
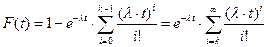
Вероятность безотказной работы:
.
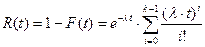Интенсивность отказов системы в целом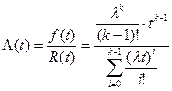 
Соотношения между моментами и параметрами распределения определяются как и у гамма-распреденения, но с заменой параметр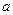а на .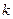
Распределение Эрланга порядка k описывает распределение случайной величины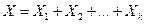 
как суммы k штук независимых случайных величин, каждая из которых распределена по показательному (экспоненциальному) закону с параметром λ.
Распределению Эрланга удовлетворяет время наработки до отказа резервированной системы с включением «холодного» резерва по способу замещения при условии, что наработка до отказа включенного элемента подчинена экспоненциальному закону. При этом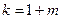 
, где m — число резервных элементов. Из соотношения 
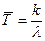вытекает свойство структур с «холодным» резервом – средняя наработка системы до отказа линейно возрастает от числа резервных элементов.
Метод вероятностной бумаги
График функции распределения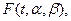 
можно представить в виде совокупности точек (t, p) на плоскости, где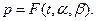 
Основная идея графического метода состоит в том, что подбирается такая непрерывная замена координат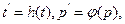 
что при этом график функции распределения 
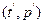, где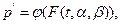 
становится прямой линией 
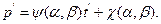Если такую замену переменных удалось отыскать, то на плоскости 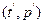любая функция распределения этого семейства будет представима в виде прямой 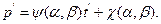Или, что то же самое, в виде прямой
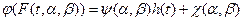……………………..(1).
Используем этот факт для оценки параметров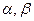 
. Предположим, что в результате испытаний получены N значений (в нашем случае N=100) некоторой случайной величины (например, времени безотказной работы элемента или интервалов между отказами в аппаратуре).
По этим значениям мы построили эмпирическую функцию распределения. Полученная эмпирическая функция при больших N лежит вблизи от теоретической функции распределения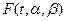 
. Тогда после замены переменных график 
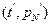будет лежать в непосредственной близости от графика 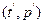, являющегося прямой вида (1). Оценив тангенс наклона k и свободный член b, и приравняв их теоретическим значениям, получаем уравнения
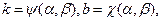……………………………………(2)
из которых находим оценки неизвестных значений параметров .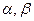
Найдем параметры a, b распределения Вейбулла:
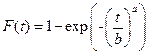
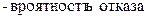
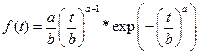
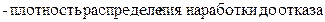
Произведем расчет параметров a и b:
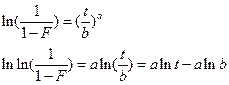
Произведем замену
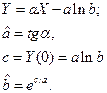
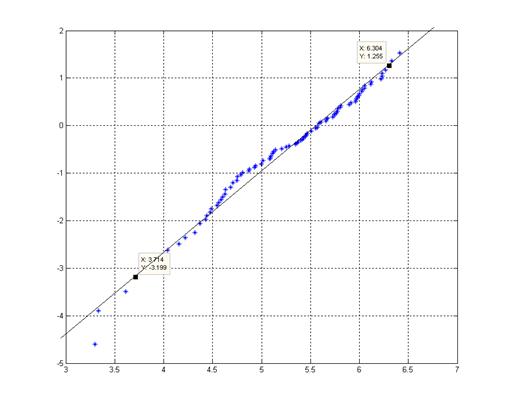
Рисунок 4: График Y(X) для метода вероятностной бумаги
Усреднив полученные значения, получили прямую, по двум точкам было построено уравнение прямой, оно имеет следующий вид:
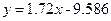
Откуда, с учетом вышеперечисленных формул, получаем:
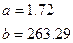
Построим график распределения Вейбулла с полученными коэффициентами:
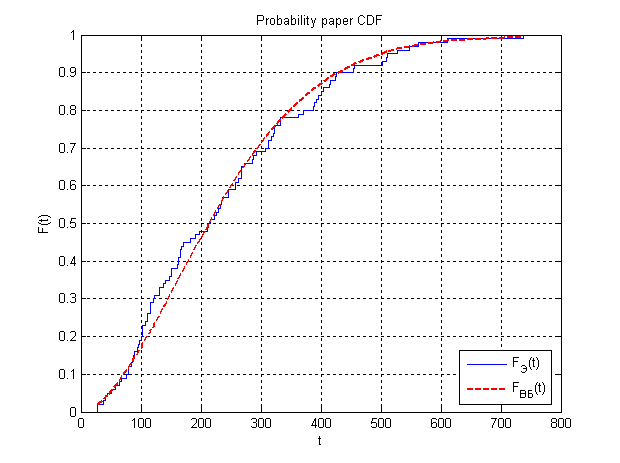
Рисунок 5: График эмпирической функции вместе с графиком распределения Вейбулла, коэффициенты которого найдены по методу вероятностной бумаги.
Произведем оценку максимальной удаленности графика распределения Вейбулла от эмпирической функции:
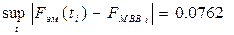
РЕФЕРАТ
Страниц __, рисунков __, источников __.
Ключевые слова: эмпирическое распределение случайной величины, начальные и центральные моменты, аппроксимирующее распределение, метод моментов, метод максимального правдоподобия, метод «вероятностной бумаги», критерии согласия.
Рассмотрены и исследованы задачи статистической обработки так называемых полных выборок в предположении их репрезентативности, то есть принадлежащих генеральной совокупности исследуемых объектов, с оценкой параметров альтернативных теоретических распределений, аппроксимирующих эмпирическую (ступенчатую) функцию распределения, двумя методами – методом моментов и методом максимального правдоподобия.
Разработано алгоритмическое и программное обеспечение для получения точечных оценок параметров двух практически важных распределений - распределения Вейбулла и гамма-распределения методом моментов и методом максимального правдоподобия. Разработан и программно реализован также алгоритм проверки выполнимости критерия А.Н. Колмогорова – критерия согласия аппроксимирующего распределения эмпирическому (ступенчатому) распределению.
Системы расчетов полностью реализованы в среде отечественного Программного комплекса «МВТУ 3.5».
Оглавление
ВВЕДЕНИЕ И ПОСТАНОВКА ЗАДАЧ ИССЛЕДОВАНИЯ.. 4
1. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ МЕТОДОВ МОМЕНТОВ И МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ.. 6
1.1. Оценка первых четырех выборочных начальных и центральных моментов и построение эмпирического распределения 6
1.2. Метод моментов. 9
1.3 Метод максимального правдоподобия (ММП) 10
1.4 О методе «вероятностной бумаги». 14
2. АЛГОРИТМЫ РАСЧЕТА ПАРАМЕТРОВ РАСПРЕДЕЛЕНИЙ МЕТОДОМ МОМЕНТОВ.. 15
2.1. Алгоритмы расчета параметров гамма-распределения методом моментов и его развитие. 15
2.2. Алгоритмы расчета параметров распределения Вейбулла. 16
3. АЛГОРИТМЫ РАСЧЕТА ПАРАМЕТРОВ РАСПРЕДЕЛЕНИЙ МЕТОДОМ МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ 18
3.1. Алгоритмы расчета параметров гамма-распределения. 18
3.2. Алгоритмы расчета параметров распределения Вейбулла для полной выборки. 21
3.3. Алгоритмы расчета параметров распределения Вейбулла для цензурированной выборки. 23
4 СТАТИСТИЧЕСКАЯ ПРОВЕРКА ГИПОТЕЗ. КРИТЕРИЙ «СТАРЕЮЩИХ» РАСПРЕДЕЛЕНИЙ.. 24
4.1 Критерий согласия А.Н. Колмогорова. 24
4.2 Критерии «стареющего» распределения. 26
5. ПРОГРАММЫ И РЕЗУЛЬТАТЫ РЕШЕНИЯ КОНКРЕТНОЙ ЗАДАЧИ ОБРАБОТКИ СТАТИСТИЧЕСКИХ ДАННЫХ 27
5.1. Постановка задачи. 27
5.2. Расчет первых четырех выборочных моментов и построение эмпирической функции распределения 28
5.3. Расчет параметров предполагаемых теоретических распределений методом моментов. 35
5.4. Расчет параметров предполагаемых теоретических распределениях методом максимального правдоподобия 50
5.5 Развитие метода максимального правдоподобия. 66
5.5 а. Метод вероятностной бумаги………………………………………………………………..
5.6 Сводка результатов, их анализ и выводы.. 70
Выводы. 76
ПРИЛОЖЕНИЕ 1 (справочное). 78
ВВЕДЕНИЕ И ПОСТАНОВКА ЗАДАЧ ИССЛЕДОВАНИЯ
Актуальность работы
При проведении работ по проблеме продления сроков службы технических объектов во всех отраслях промышленности, в частности в атомной энергетике, широко используются статистические методы оценки фактических показателей надежности по эксплуатационным данным о наработках и отказах и прогнозирования надежности на продлеваемый срок эксплуатации. В директивном порядке используется Руководящий документ Государственного комитета по стандартам РД 50-690-89 [1].
РД 50-690-89, выпущенный взамен ранее действовавших государственных стандартов ГОСТ 27.201-81, ГОСТ 27.502-83, ГОСТ 27.503-81, ГОСТ 27.504-84, устанавливает методы планирования определительных испытаний на надежность и методы оценки показателей надежности оборудования, в том числе по результатам эксплуатационных наблюдений.
Прогнозирование надежности требует, как известно, «разгадки» соответствующих вероятностных распределений (как правило двухпараметрических) и определение их параметров. Теоретической основой при этом являются широко известные метод моментов (К. Пирсон) и метод максимального правдоподобия (Р. Фишер).
Классический метод моментов основан на сопоставлении эмпирических моментов, найденных по статистическим данным эксплуатации, с теоретическими моментами, связанными аналитическими выражениями с параметрами рассматриваемых распределений [2]. При этом используются два первых момента – точечные оценки математического ожидания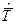 
и дисперсии 
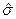, являющиеся при правильной обработке информации состоятельными и несмещенными. Так, например, для гамма - распределения с плотностью вероятности 
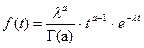имеют место соотношения (уравнения) 
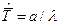и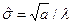 
, которые легко разрешаются относительно 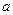и 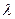. Однако имеющаяся важная экспериментальная информация об оценках коэффициентов асимметрии 
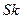и эксцесса 
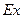совершенно не используется. И в этой связи актуальной для практики задачей является развитие классических методов, в частности методов моментов и максимального правдоподобия.
Цель работы - развитие вычислительных процедур и алгоритмов и разработка программного обеспечения статистической обработки информации, получаемой из сферы эксплуатации, для решения задач объективной оценки характеристик и показателей надежности оборудования с использованием методов моментов, вероятностной бумаги и максимального правдоподобия для полных и цензурированных выборок без обращения к огромному числу таблиц.
Задачи работы:
1. Анализ и практическое освоение известных классических методов и алгоритмов обработки статистических данных для информационно-аналитических систем различного назначения.
2. Разработка эффективных алгоритмов и программ реализации методов моментов, максимального правдоподобия и вероятностной «бумаги» для обработки статистической информации по полным и цензурированным выборкам.
3. Отработка алгоритмов и программ статистической проверки гипотез о теоретическом законе распределения с применением критерия согласия А.Н. Колмогорова и системы неравенств, устанавливающих принадлежность функции распределения к классу функций с возрастающей интенсивностью «опасности» (или интенсивностью отказов для технических систем).
4. Решение конкретных задач обработки экспериментальных (наблюдаемых) данных с «распознаванием» теоретической функции распределения и оценкой ее параметров.