Методы оценки параметров одновременных уравнений
Коэффициенты структурной модели могут быть оценены разными методами в зависимости от вида системы одновременных уравнений.
Наиболее из них распространены следующие методы оценки:
косвенный МНК (КМНК);
двухшаговый МНК (ДМНК);
трехшаговый МНК (ТМНК);
метод максимального правдоподобия с полной информацией;
метод максимального правдоподобия при ограниченной информации.
Косвенный и двухшаговый МНК рассматриваются как традиционные методы оценки коэффициентов структурной модели.
КМНК применяется для идентифицируемой системы одновременных уравнений, а ДМНК используется для оценки коэффициентов сверхидентифицируемой модели.
Метод максимального правдоподобия рассматривается как наиболее общий метод оценивания, результаты которого при нормальном распределении признаков совпадают с МНК, но при большом числе уравнений системы этот метод приводит к достаточно сложным процедурам вычислений.
Дальнейшим развитием ДМНК является ТМНК. Этот метод пригоден для оценки параметров всех видов уравнений структурной модели. Однако при некоторых ограничениях на параметры более эффективен ДМНК.
Процедура применения косвенного метода наименьших квадратов (КМНК) предполагает выполнение следующих этапов:
преобразование структурной модели в приведенную форму;
для каждого уравнения приведенной формы модели обычным МНК оцениваются приведенные коэффициенты 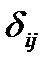 .
.
коэффициенты приведенной формы модели трансформируются в параметры структурной модели.
Рассмотрим применение КМНК для простейшей идентифицируемой модели:
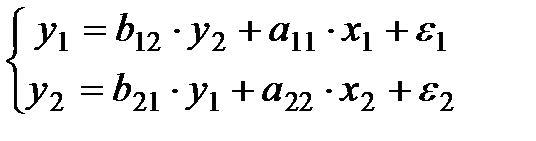 ;
;
Приведенная форма модели имеет вид:
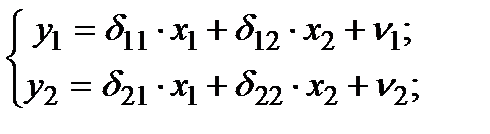
где 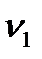 ,
, 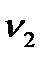 - случайные ошибки приведенной формы.
- случайные ошибки приведенной формы.
Применяя, для каждого уравнения этой системы, МНК определяем коэффициенты 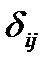 .
.
Соответствующие системы будут выглядеть следующим образом:
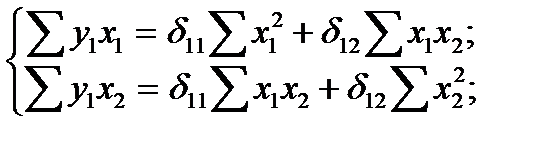 (4.3)
(4.3)
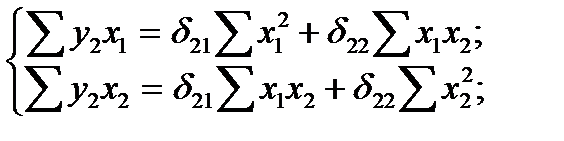 (4.4)
(4.4)
Решая системы (4.3), (4.4) находим коэффициенты 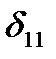 ,
, 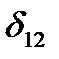 ,
, 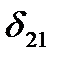
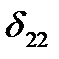 .
.
От полученной приведенной формы модели переходим к структурной форме модели. Для этого из 2-го уравнения системы (4.2) выражаем х  и подставляем в 1-е уравнение, получим 1-е уравнение системы (4.1). И наоборот, выражая из 1-го уравнения системы (4.2) х
и подставляем в 1-е уравнение, получим 1-е уравнение системы (4.1). И наоборот, выражая из 1-го уравнения системы (4.2) х  и подставляя во 2-е уравнение, получаем 2-е уравнение системы (4.1).
и подставляя во 2-е уравнение, получаем 2-е уравнение системы (4.1).
При непосредственном применении традиционного МНК к каждому уравнению структурной формы результаты могут сильно отличаться от результатов применения КМНК.
Если система сверхидентифицируема, то КМНК не даст однозначных оценок параметров структурной модели и поэтому он не используется. В этом случае можно использовать разные методы, среди которых наиболее распространен ДМНК.
Основная идея ДМНК – получение на основе приведенной формы модели для сверхидентифицируемого уравнения теоретических значений эндогенных переменных, содержащихся в правой части уравнения.
Затем, подставив их вместо фактических значений, можно применить обычный МНК к структурной форме сверхидентифицируемого уравнения.
Если все уравнения системы сверхидентифицируемы, то для оценки структурных коэффициентов каждого уравнения используется ДМНК.
Если в системе есть точно идентифицируемые уравнения, то структурные коэффициенты по ним находятся из системы приведенных уравнений.
Пусть дана идентифицируемая модель:
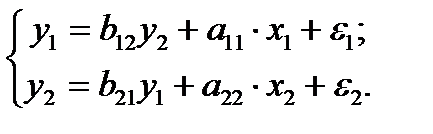 (4.5)
(4.5)
Если на параметр b 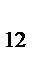 наложить ограничение, а именно
наложить ограничение, а именно 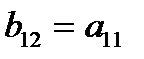 , то система превращается в простейшую сверхидентифицируемую модель
, то система превращается в простейшую сверхидентифицируемую модель
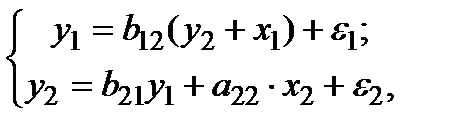 (4.6)
(4.6)
в которой 1-е уравнение уже является сверхидентифицируемым:
Н=1 (у 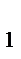 ), D=1 (х
), D=1 (х 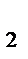 ), значит D+1>H.
), значит D+1>H.
Второе уравнение является (как и было) точно идентифицируемым:
Н=2 (у 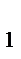 , у
, у 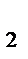 ), D=1 (х
), D=1 (х 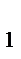 ), D+1=H.
), D+1=H.
Применим ДМНК к полученной модели (4.6):
1 шаг: применив МНК, найдем приведенную форму модели:
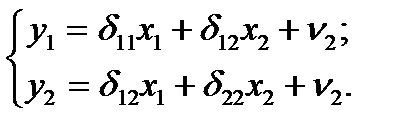
2 шаг: на основе 2-го уравнения данной системы, подставляя заданные значения х 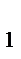 и х
и х 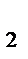 , определяем теоретические значения для эндогенной переменной у
, определяем теоретические значения для эндогенной переменной у 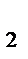 , т.е. у
, т.е. у 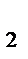 .
.
Введем новую переменную Z: Z= у 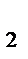 + х
+ х 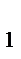 .
.
Тогда 1-е уравнение системы (4.6) 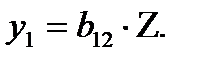
Применяя МНК к данному уравнению, находим 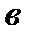
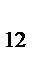 : S у
: S у 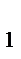 Z=
Z= 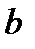
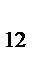 SZ
SZ 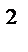 откуда
откуда 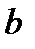
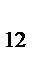 =S у
=S у 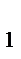 Z/SZ
Z/SZ  .
.
2-е уравнение системы (4.6) не изменилось, поэтому система одновременных уравнений будет иметь вид:
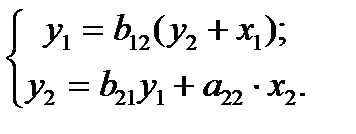
Приведем некоторые примеры применения эконометрических систем уравнений на практике.
К одной из распространенных систем одновременных уравнений относится статическая модель Кейнса, для описания народного хозяйства страны:
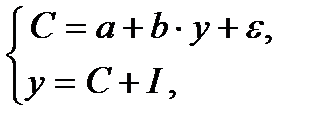
где С – личное потребление, у – национальный доход, I – инвестиции (все в постоянных ценах).
Другим примером может служить динамическая модель Кейнса:
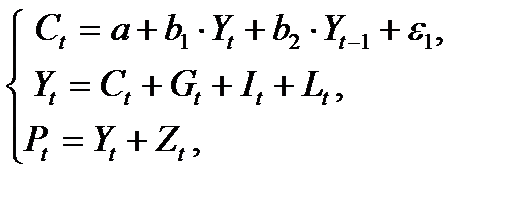
где У 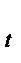 ,С
,С 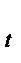 , P
, P 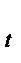 - доход, частное потребление, ВНП, соответственно, в период времени t; У
- доход, частное потребление, ВНП, соответственно, в период времени t; У 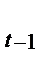 - доход предыдущего года; G
- доход предыдущего года; G 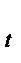 , I
, I 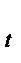 , L
, L 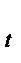 , Z
, Z 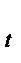 - соответственно, общественное потребление, валовые капиталовложения, изменения складских запасов, сальдо платежного баланса.
- соответственно, общественное потребление, валовые капиталовложения, изменения складских запасов, сальдо платежного баланса.
Большую популярность получила динамическая модель Клейна.
Система одновременных уравнений нашла применение в исследованиях спроса и предложения. Она имеет вид:
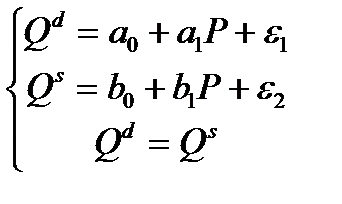
где Q 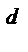 , Q
, Q 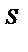 - объем спроса и объем предложения, Р - цена.
- объем спроса и объем предложения, Р - цена.
Построение системы структурных уравнений позволяет глубже изучить причины связи результирующих признаков. При этом происходит выделение и оценка косвенных и непосредственных влияний признаков.
