Частные уравнения множественной регрессии. Индексы множественной и частной корреляции и их расчет

На основе линейного уравнения множественной регрессии 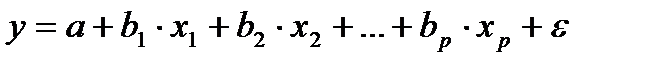могут быть найдены частные уравнения регрессии:

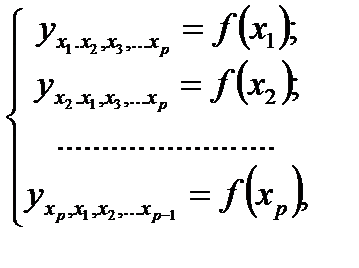
т.е. уравнения регрессии, которые связывают результативный признак с соответствующими факторами х_i при закреплении других учитываемых во множественной регрессии факторов на среднем уровне. В случае линейной регрессии частные уравнения имеют следующий вид:

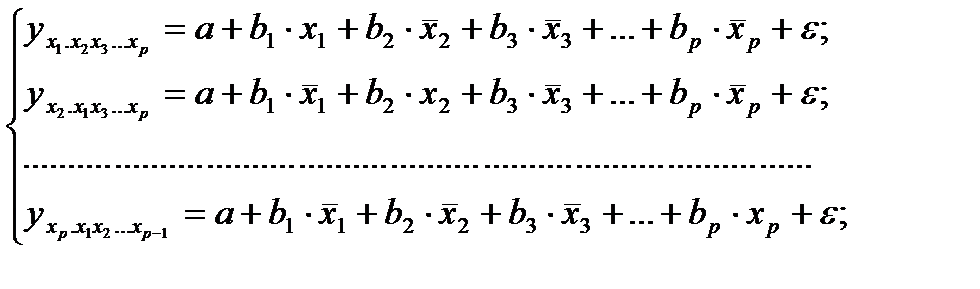
Подставляя в эти уравнения средние значения соответствующих факторов получаем систему уравнений линейной регрессии, т.е. имеем:

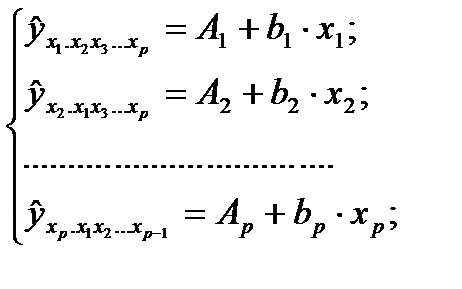
где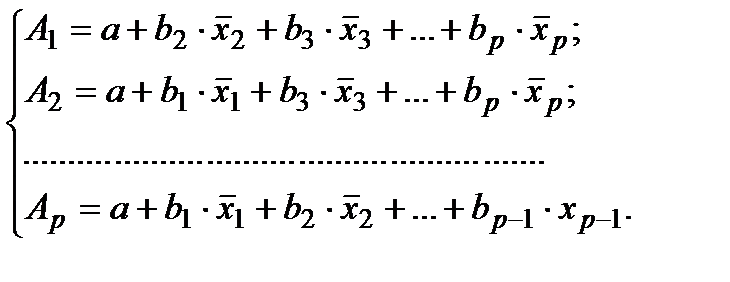

Частные уравнения регрессии характеризуют изолированное влияние фактора на результат, ибо другие факторы закреплены на низменном уровне. Эффекты влияния других факторов присоединены в них к свободному члену уравнения множественной регрессии (А_i).Это позволяет на основе частных уравнений регрессии определять частные коэффициенты эластичности

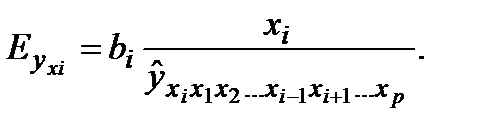
На основании данной информации могут быть найдены средние по совокупности показатели эластичности: .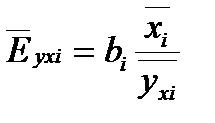

Практическая значимость уравнения множественной регрессии оценивается с помощью показателя множественной корреляции и его квадрата – коэффициента детерминации. Показатель множественной корреляции характеризует тесноту совместного влияния факторов на результат.

Независимо от вида уравнения индекс множественной корреляции рассчитывается по формуле:

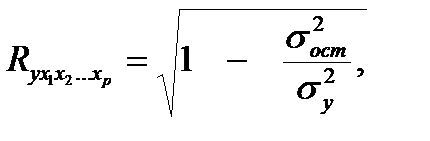
где 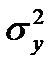- общая дисперсия результативного признака,

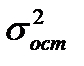- остаточная дисперсия для уравнения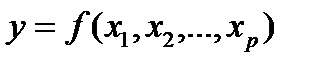

.

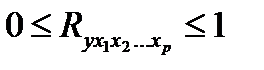Чем ближе его значение к 1, тем теснее связь результативного признака со всем набором исследуемых факторов.

Для расчета индекса множественной корреляции можно пользоваться и следующей формулой:

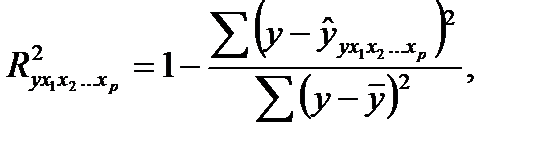
где у - фактические значения результативного показателя;

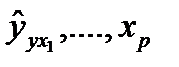- значения результативного показателя, рассчитанные по уравнению регрессии;

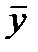- среднее арифметическое значение результативного показателя.

Сравнивая индексы множественной регрессии и парной корреляции, можно сделать вывод о целесообразности включения в уравнение регрессии того или иного фактора. В частности, если дополнительно включенные в уравнение множественной регрессии факторы третьестепенны, то индекс множественной корреляции практически совпадает с индексом парной корреляции.

Частные коэффициенты (или индексы) корреляции характеризуют тесноту связи между результатом и соответствующим фактором при устранении влияния других факторов, включенных в уравнение регрессии.

Рассмотрим пример. Пусть зависимость объема продукции у от затрат труда х задается уравнением:

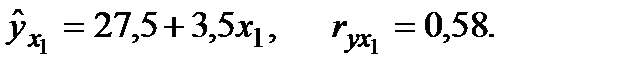
Допустим, что дополнительный фактор х₂- техническая оснащенность производства – преобразовал уравнение к виду:

.

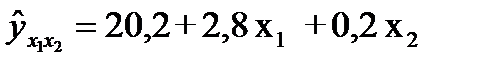Тогда остаточные дисперсии 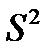для этих уравнений определяются соответственно следующими формулами:

; .

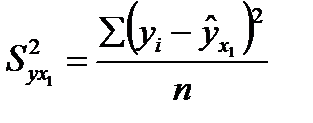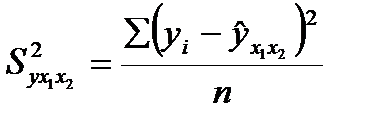Предположим, что ; .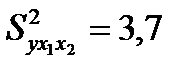

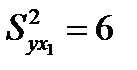Уменьшение остаточной дисперсии за счет дополнительного включения фактора x₂ составит:

.

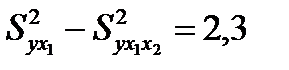Чем больше доля полученной разности в остаточной вариации, тем теснее связь между у и x₂ , при неизменности действия фактора x₁

Величина, рассчитываемая формулой:

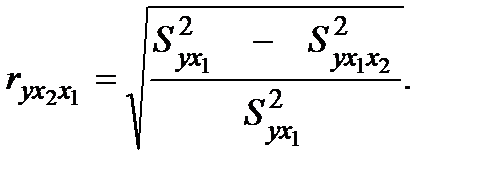
называется индексом частной корреляции для фактора х₂:

Аналогично определяется индекс частной корреляции для фактора x_1.

.

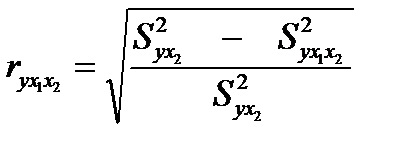Если в нашем примере предположить, что 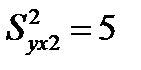, то частные коэффициенты корреляции составят: 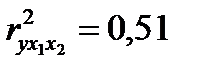; 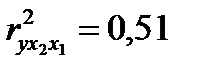. На их основе можно делать вывод: более сильное воздействие на объем продукции оказывает техническая оснащенность предприятий.

В общем случае при наличии р факторов формула для расчета индекса частной корреляции имеет вид:

где 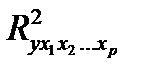- множественный коэффициент детерминации всего комплекса р факторов с результатом,

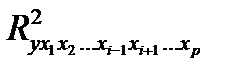- тот же показатель детерминации, но без введения в модель фактора x_j.

Значимость уравнения множественной регрессии в целом, так же как и в парной регрессии, оценивается с помощью F - критерия Фишера:

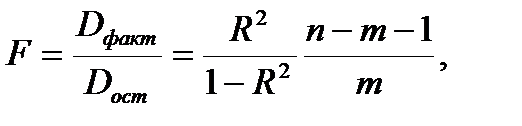
где R² - коэффициент (индекс) множественной детерминации;

m - число параметров при переменных х;

n - число наблюдений.

Если оценивается значимость влияния фактора х_i в уравнении регрессии, то определяется частный F - критерий:

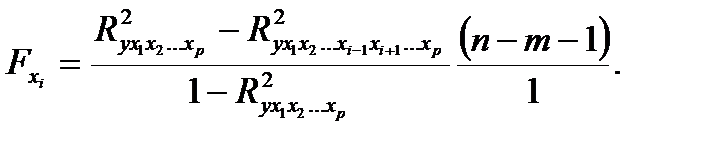
Значимость коэффициентов чистой регрессии производится по t - критерию Стьюдента.

Если до сих пор в качестве факторов мы рассматривали только экономические переменные, принимающие количественные значения, то возможно, может оказаться необходимым включить в модель фактор, имеющий два или более качественных уровней. Например, такие атрибутивные признаки как профессия, пол, образование климатические условия и т.д. имеют несколько качественных уровня. Чтобы ввести такие переменные в модель необходимо их преобразовать в количественные переменные. Переменные такой конструкции называются фиктивными.

Рассмотрим пример. Предположим, что по группе лиц мужского и женского пола изучается линейная зависимость потребления кофе от цены.

В общем виде данное уравнение имеет вид: ,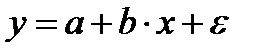

где y - количество потребляемого кофе, x - цена.

Аналогичные уравнения могут быть найдены отдельно для лиц мужского пола:

;

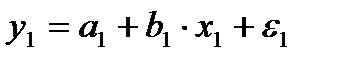женского пола:

.

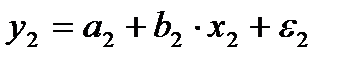Различия в потреблении кофе проявятся в различии средних `у<sub>1</sub> и`у₂. Вместе с тем сила влияния х на у может быть одинаковой, т.е. .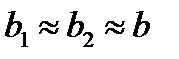

В этом случае можно ввести общее уравнение регрессии с включением в него фактора «пол» в виде фиктивной переменной:

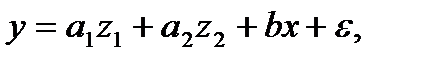
где z₁, z₂ – фиктивные переменные.

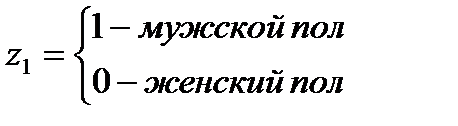
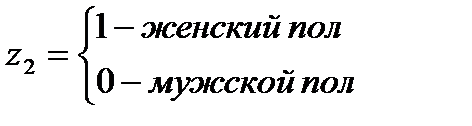
Рассмотренная модель с фиктивными переменными, выступающими как факторы, обладает наибольшими прогностическими возможностями. Однако на практике может возникнуть необходимость построения модели, в которой фиктивная переменная должна играть роль результата. Подобного рода модели применяются в социологии, при обработке данных социологических опросов. В качестве у - рассматриваются ответы на вопросы, данные в альтернативной форме: «да» или «нет», т.е. зависимая переменная у, имеет два значения 1 - («да») и 0 - («нет»).