Минимизация продолжительности поисковой процедуры.

ПРОГРАММА, КОНТРОЛЬНЫЕ ЗАДАНИЯ

И МЕТОДИЧЕСКИЕ УКАЗАНИЯ

по дисциплине «Теория скрытности»

по направлению 11.03.01 «Радиотехника»,

профилю «Радиотехнические средства передачи,

приема и обработки сигналов»

для студентов заочной формы обучения

Воронеж 2016

Составитель канд. техн. наук В.П. Литвиненко

УДК 621.391

Программа, контрольные задания и методические указания по дисциплине «Теория скрытности» для подготовки бакалавров, обучающихся по направлению 11.03.01 «Радиотехника», профилю «Радиотехнические средства передачи, приема и обработки сигналов»заочной формы обучения / ФГБОУ ВПО «Воронежский государственный технический университет»; сост. В.П. Литвиненко. Воронеж, 2016. 28 с.

Приведены программа, контрольные задания и методические указания к контрольной работе и лабораторным занятиям по дисциплине «Теория скрытности».

Контрольная и лабораторные работы выполняются с помощью современной вычислительной техники на основе разработанной на кафедре радиотехники программы Poisk.exe. Предусматривается использование пакета программ MathCAD и других систем программирования.

Методические указания предназначены для студентов третьего курса.

Табл. 2. Ил. 3. Библиогр.: 5 назв.

Рецензент д-р. техн. наук, проф. А.Б. Токарев

Ответственный за выпуск зав. кафедрой канд. техн. наук, проф. Б.В. Матвеев

Печатается по решению редакционно-издательского совета Воронежского государственного технического университета

Ó ФГБОУ ВПО «Воронежский государственный технический университет», 2016

ВВЕДЕНИЕ

Дисциплина «Теория скрытности» введена решением Совета ВГТУ в рамках профиля «Радиотехнические средства передачи, приема и обработки сигналов»по направлению 11.03.01 «Радиотехника».

Целью дисциплины «Теория скрытности» является изучение методов оценки и анализа скрытности и защищенности от радиоразведки радиосигналов и систем радиосвязи, исследование алгоритмов поиска состояния объекта и методов их оптимизации.

Задачи дисциплины состоят в освоении методов анализа разведывательной защищенности систем связи, проектирования эффективных поисковых процедур и их оптимизации в различных технических задачах разведки, диагностики, поиска сигналов и синхронизации.

СОДЕРЖАНИЕ РАБОЧЕЙ ПРОГРАММЫ

ПРЕПОДАВАНИЯ ДИСЦИПЛИНЫ

Требования к уровню освоения содержания

дисциплины

В результате изучения дисциплины формируются следующие компетенции обучающегося:

- ОПК‑2 - способность выявлять естественнонаучную сущность проблем, возникающих в ходе профессиональной деятельности, привлекать для решения соответствующий физико-математический аппарат;

- ПК-1 - способность выполнять математическое моделирование объектов и процессов по типовым методикам, в том числе с использованием стандартных пакетов прикладных программ;

- ПВК‑1 - способность оценивать скрытность сигналов и систем радиосвязи, энергетическую защищенность радиолиний, проводить вероятностные расчеты различных видов скрытности.

Студент должен знать методы оценки скрытности, алгоритмы поиска состояния объекта и методы их оптимизации, влияние на скрытность помех и маскирующих сигналов, характеристики скрытности различных сигналов и систем радиосвязи. Студент должен уметь проводить расчеты скрытности состояния объекта в различных условиях, проектировать оптимальные поисковые процедуры, выполнять сравнительный анализ скрытности сигналов. Студент должен приобрести навыки проведения расчетов скрытности и моделирования поисковых процедур, в том числе и с использованием современной вычислительной техники.

Содержание дисциплины

Дисциплина «Теория скрытности» изучается в пятом семестре в соответствии с учебным планом (табл. 1).

Таблица 1

Семестр	Лекции час.	Лаб. раб. час.	Конт. раб. час.	Экзамен час.

В учебной литературе материал по теории скрытности освящен слабо. Основное внимание следует сосредоточить на учебных пособиях [1-3].

Необходимо восполнить имеющиеся пробелы в теории вероятностей и математической статистике. Основное внимание следует уделить понятиям теории скрытности, поисковым процедурам, расчету их характеристик и оптимизации. При выполнении лабораторных работ и контрольных заданий предполагается широкое использование вычислительной техники.

Контрольная работа включает в себя четыре задания по расчету скрытности, исследованию и оптимизации алгоритмов поиска.

Перечень лабораторных работ:

1) исследование алгоритмов последовательного и дихотомического поиска.

2) оптимизация алгоритмов поиска.

Лабораторные работы выполняются с помощью специальной программы Poisk в дисплейном классе кафедры или на домашней ЭВМ. Студенты могут работать с ней самостоятельно при изучении теоретического материала и в ходе подготовки к лабораторным работам.

СОДЕРЖАНИЕ РАЗДЕЛОВ ДИСЦИПЛИНЫ

2.1 Введение, исходные положения.

Предмет и задачи теории скрытности. Исторический

очерк, примеры. Обобщенная модель скрытного объекта. Подходы к оценке скрытности. Поисковая процедура, определение скрытности. Двоичные измерения, дерево поиска. Определение скрытности, ее мера. Простейшие примеры. Количество информации, энтропия. Кривая снятия неопределенности (КСН), декремент неопределенности, остаточная энтропия. Применение КСН для оценки скрытности. Энтропийная скрытность.

Вопросы для самопроверки.

1. Дайте качественное описание скрытных объектов в области радиосвязи и других областях человеческой деятельности.

2. Сформулируйте определение скрытности, объясните его физический смысл, приведите примеры.

3. Что такое двоичные измерения, как они могут проводиться для различных скрытных объектов?

4. Что такое энтропия множества состояний объекта? Объясните понятия неопределенности состояния, количества информации о состоянии объекта, получаемого в процессе поиска.

5. Что представляет собой кривая снятия неопределенности (КСН), каков ее смысл, что означает декремент неопределенности?

6. Как определяется энтропийная скрытность?

СРЕДСТВА ОБЕСПЕЧЕНИЯ ОСВОЕНИЯ ДИСЦИПЛИНЫ

Программа «Poisk» позволяет проводить исследования алгоритмов поиска при проведении лабораторных работ и в

ходе самостоятельной работы. Для проведения расчетов рекомендуется использовать пакет программ «MathCad».

КОНТРОЛЬНАЯ РАБОТА

Общие методические указания

При изучении дисциплины «Основы теории скрытности» предусматривается выполнение одной контрольной работы, включающей в себя четыре задания.

Перед началом выполнения заданий необходимо изучить соответствующий теоретический материал.

Для проведения вычислений необходимо использовать современные программные средства, например, пакет программ MathCAD. Весьма целесообразно написать самостоятельную программу расчетов на каком либо языке высокого уровня. В отчете необходимо привести соответствующие листинги программ (для задания 1 пример программы в пакете MathCAD приведен в приложении Б).

Оформление контрольных работ осуществляется в строгом соответствии с требованиями стандарта предприятия(СТП) [5].

Защита контрольной работы проводится после ее проверки преподавателем в виде собеседования.

4.2.Задание 1 «Энтропийная скрытность»

В соответствии с указанным преподавателем номером варианта выберите из таблицы П1 приложения А распределе-

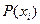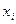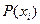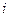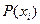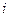ние вероятностей состояний объекта и его параметры. Вычислите значения в заданном диапазоне номеров , представьте зависимость от графически. Рассчитайте энтропийную скрытность множества состояний.

Определите энтропийную скрытность множества состояний с тем же арсеналом 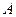, но с равномерным распределением вероятностей состояний вида

, . (1)

Сравните полученные значения энтропийной скрытности, объясните полученные результаты.

4.3.Задание 2 «Последовательный поиск»

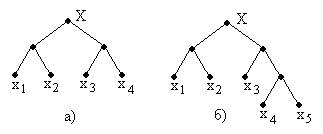
Для заданного распределения вероятностей 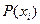определите алгоритмическую скрытность состояний объекта для показанного на рис. 1а. дерева поиска. Проведите аналогичный расчет для дерева поиска на рис. 1б. Повторите эти расчеты для равномерного распределения вероятностей (1). Сравните и объясните полученные результаты.

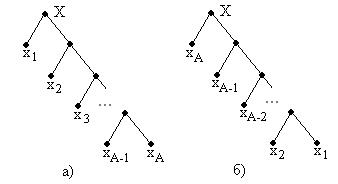
Рис. 1.

Для заданного распределения вероятностей 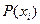определите и постройте графически дерево поиска для оптимального последовательного алгоритма (состояния объекта проверяются последовательно по мере уменьшения их вероятностей). Вычислите соответствующую ему алгоритмическую скрытность.

4.4.Задание 3 «Дихотомический поиск»

Для заданного в соответствии с вариантом распределения вероятностей 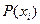определите скрытность при дихотомическом поиске, дерево которого показано на рис. 2. Дерево поиска на рис.2а соответствует случаю, когда 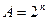, 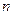- целое число (в примере 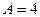), а если это условие не выполняется, то дерево поиска имеет вид, показанный на рис. 2б (в примере ).

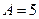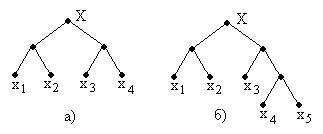
Рис. 2.

При том же значении 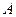определите скрытность для равномерного распределения вероятностей (1). Проанализируйте результаты.

Сравните между собой полученные значения скрытности при дихотомическом и последовательном алгоритмах поиска (задание 2).

4.5.Задание 4 «Оптимизация поиска»

Методом Циммермана – Хаффмена для заданного в соответствии с вариантом распределения вероятностей 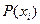постройте оптимальное дерево поиска и рассчитайте потенциальную скрытность. Выполните это же задание методом Шеннона – Фано, сравните полученные деревья поиска.

Проведите аналогичные расчеты для равномерного (1) распределения вероятностей 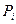. Сравните результаты, сделайте выводы.

Сравните потенциальную скрытность с полученными ранее значениями энтропийной скрытности и алгоритмической скрытности при последовательном и дихотомическом алгоритмах поиска для равномерного (1) и заданного распределений вероятностей состояний объекта.

Последовательный поиск

5.2.1. Установите равномерное распределение вероятностей событий при их числе 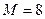для четного и 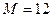для нечетного вариантов. Задайте максимальное число измерений 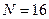. На наборном поле задайте полный алгоритм поиска «n=m», при котором номер события 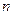равен номеру измерения 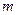(последнее событие не проверяется). Проведите моделирование, определите среднее число измерений 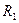. Результат внесите в табл. 2.

Таблица 2.

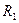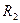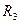моделирование
расчет

На наборном поле включите проверку последнего события, определите среднее число измерений 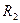, запишите его в табл. 2, проанализируйте результаты. Проведите расчет скрытносте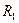й и .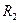

Задайте алгоритм поиска «n=M-m+1», при котором первым проверяется последнее событие, а последним – второе (первое событие не проверяется). По результатам моделирования определите среднее число измерений 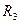, запишите его в табл. 2, проведите расчет 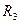, сделайте выводы.

5.2.2. Установите экспоненциальное распределение вероятностей событий (второе в распахивающемся списке) вида 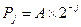, , 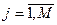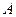- нормирующий множитель, при том же 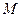, что и в пункте 6.2.1. На наборном поле установите алгоритм поиска «n=m» без проверки последнего события. Определите среднее число измерений 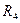, запишите его в табл. 3. Проведите расчет величины .

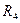Задайте алгоритм поиска «n=M-m+1» (первое событие не проверяется). По результатам моделирования найдите среднее число измерений 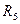, запищите его в табл. 3, проанализируйте результаты.

Таблица 3.

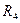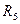5.2.3. Выберите из распахивающегося списка распределение вероятностей в соответствии со своим вариантом задания при числе событий 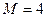. Пример рабочего окна показан на рис. 8.

Задайте алгоритм поиска «n=m» без проверки последнего события. Проведите моделирование. С помощью перехвата экрана «Print Screen» сохраните в отчете результаты работы.

Проанализируйте КСН, ее оптимальность, объясните ход кривой. Среднее число измерений 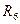внесите в табл. 4.

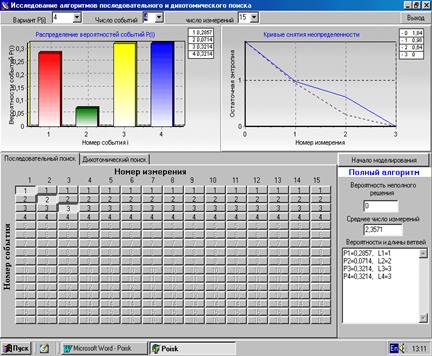Рис. 8.

Таблица 4.

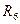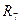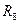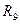5.2.4. Повторите эксперименты по пункту 6.2.3 для числа событий M=8, 12 и 16. Занесите в отчет результаты, значения среднего числа измерени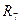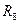й , и 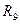запишите в табл. 3. Проведите сравнительный анализ.

Дихотомический поиск

5.2.5. Установите число событий 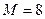для четного варианта и 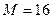для нечетного при равномерном распределении вероятностей и задайте число измерений 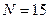. Временно включите режим последовательного поиска при алгоритме «n=m», проведите моделирование. Переключитесь в режим дихотомического поиска. В правой верхней части экрана останется график КСН последовательного поиска (пунктир).

Задайте с помощью наборного поля дихотомический алгоритм поиска, выполните моделирование. Проведите перехват экрана. Проанализируйте графики КСН для дихотомического и последовательного алгоритмов поиска.

5.2.6. Выберите экспоненциальное распределение вероятностей событий вида 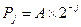, , 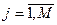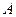- нормирующий множитель, при том же 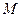, что и в пункте 6.2.5. Задайте дихотомический алгоритм поиска в этом случае. Проведите моделирование, проанализируйте результаты.

5.2.7. Выберите распределение вероятностей событий в соответствии с вариантом задания при 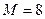. На наборном поле установите алгоритм дихотомического поиска. Проведите моделирование с последующим перехватом экрана.

Задайте алгоритм последовательного поиска «n=m», выполните моделирование с последующим перехватом экрана. Проанализируйте полученные результаты, сравните КСН рассмотренных алгоритмов поиска.

5.3. Лабораторная работа 2 «Оптимизация алгоритмов поиска»

5.3.1. Включите режим дихотомического поиска. Установите число событий 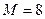для четного и 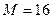для нечетного варианта при равномерном распределении вероятностей и задайте число измерений 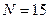. Разработайте опти-

мальный алгоритм поиска, задайте его на наборном поле, проведите моделирование, определите потенциальную скрытность. Проведите расчет потенциальной и энтропийной скрытностей, сравните результаты.

5.3.2. Выберите экспоненциальное распределение вероятностей событий вида 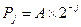, , 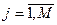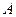- нормирующий множитель, при том же 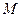, что и в пункте 5.3.1. Определите оптимальный алгоритм поиска, задайте его на наборном поле, проведите моделирование, определите потенциальную скрытность. Проведите сравнительный анализ результатов по пунктам 5.3.1 и 5.3.2.

5.3.3. Для экспоненциального распределения вероятностей из пункта 5.3.2 последовательно уменьшая максимальное число измерений от 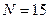до 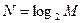, разработайте оптимальные алгоритмы поиска и по результатам моделирования определите соответствующие значения среднего числа измерений 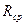. Результаты внесите в табл. 5.

Таблица 5.

N			…
Rср

Постройте график зависимости 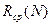. Проведите анализ результатов. Как изменяется оптимальный алгоритм поиска при ограничении максимального числа измерений.

5.3.4. Для своего варианта распределения вероятностей при числе событий 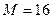разработайте оптимальный алгоритм поиска, постройте дерево поиска, объясните его форму, чем она обусловлена?

На наборном поле задайте оптимальный полный алгоритм поиска. Последовательно исключая последние измерения (до 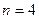), рассмотрите зависимость среднего числа измерений 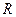, вероятности неполного решения 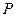и остаточной

скрытности 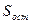от продолжительности поиска 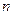. Результаты запишите в табл. 6, постройте графики. Проведите сравнительный анализ полученных результатов.

Таблица 6.

n			…
R
P
Sост

ПРИЛОЖЕНИЕ А

Варианты распределения вероятностей

Таблица П1

№	Распределение вероятностей	Значения параметров
	,
	,
	,
	,
	,
	,
	,

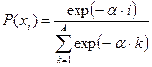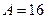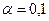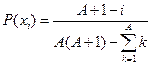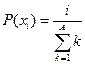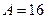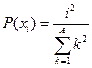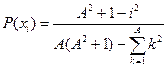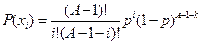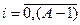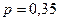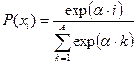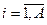Продолжение таблицы П1

	,
	,
	,
	,
	,
	,
	,

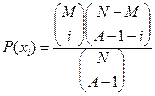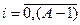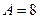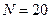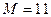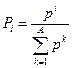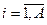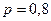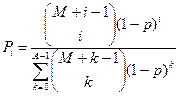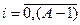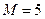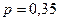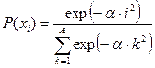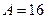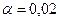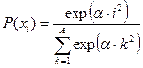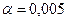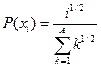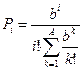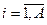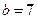Продолжение таблицы П1

	,
	,
	,
	,
	,
	,
	,
	,

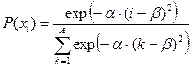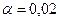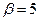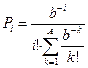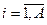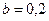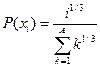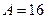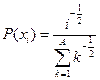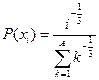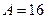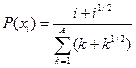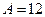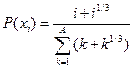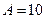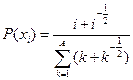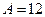Продолжение таблицы П1

	,
	,
	,
	,
	,
	,
	,
	,

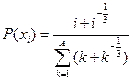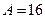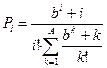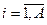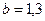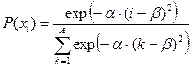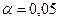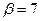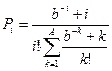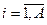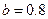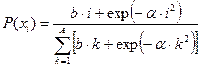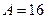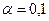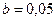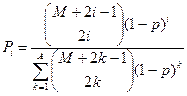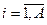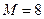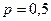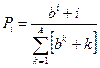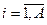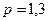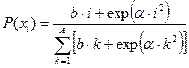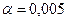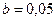Продолжение таблицы П1

	,
	,
	,
	,
	,
	,
	,
	,

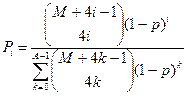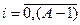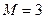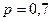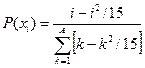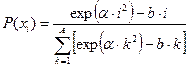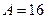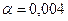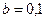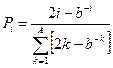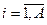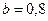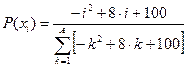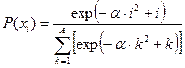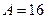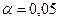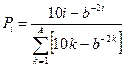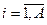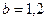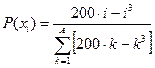ПРИЛОЖЕНИЕ Б

Пример программы для выполнения первого задания

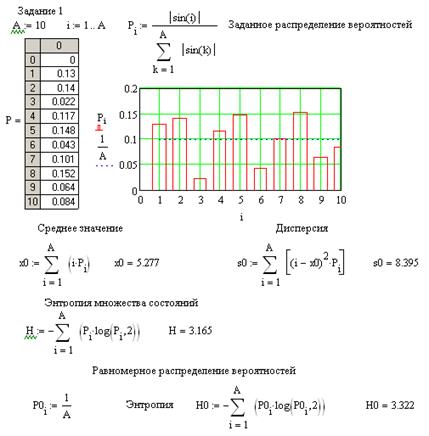
ПРИЛОЖЕНИЕ В

Биномиальные коэффициенты

В выражениях для распределения вероятностей (приложение А) используются биномиальные коэффициенты, равные

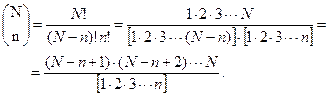
БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Каневский З.М., Литвиненко В.П., Макаров Г.В., Максимов Д.А. Основы теории скрытности: Учеб. пособие/ Воронеж. гос. техн. ун-т. Воронеж, 2006. 202с.

2. Литвиненко В.П. Энергетическая скрытность сигналов и защищенность радиолиний. Учеб. пособие / Воронеж. гос. техн. ун-т. Воронеж, 2009. 166с.

3. Литвиненко В.П. Основы теории скрытности: практикум. Учеб. пособие / Воронеж. гос. техн. ун-т. Воронеж, 2010. 106с.

4. Палий А.И. Радиоэлектронная борьба. М., Связь, 1989, 430с..

5. Стандарт предприятия (СТП ВГТУ 005-2007). Дипломное проектирование. Оформление расчетно-пояснительной записки и графической части. Воронеж: ВГТУ, 2007. 34 с.

СОДЕРЖАНИЕ

ВВЕДЕНИЕ ……………………………………….…..... 1

1. СОДЕРЖАНИЕ РАБОЧЕЙ ПРОГРАММЫ

ПРЕПОДАВАНИЯ ДИСЦИПЛИНЫ ……………… 1

2. СОДЕРЖАНИЕ РАЗДЕЛОВ ДИСЦИПЛИНЫ …… 3

3. СРЕДСТВА ОБЕСПЕЧЕНИЯ ОСВОЕНИЯ

ДИСЦИПЛИНЫ ……………….…………………..… 7

4. КОНТРОЛЬНАЯ РАБОТА ………………………….. 7

4.1. Общие методические указания …….……………… 7

4.2. Задание 1 «Энтропийная скрытность» ……...……. 7

4.3. Задание 2 «Последовательный поиск» …….......…. 8

4.4. Задание 3 «Дихотомический поиск» ……………… 9

4.5. Задание 4 «Оптимизация поиска» …..…………… 10

5. МЕТОДИЧЕСКИЕ УКАЗАНИЯ К

ЛАБОРАТОРНЫМ РАБОТАМ ……………….….... 10

5.1. Описание рабочей программы ………..…………. 10

5.1.1. Общее описание программы …………………… 10

5.1.2. Режим последовательного поиска …………...… 12

5.1.3. Режим дихотомического поиска …….………… 13

5.2. Лабораторная работа 1 «Исследование

алгоритмов последовательного и дихотомичес-

кого поиска» …………………………………...…. 15

5.3. Лабораторная работа 2 «Оптимизация

алгоритмов поиска» ……………...……………….. 18

ПРИЛОЖЕНИЕ А ………………..………...………….. 21

ПРИЛОЖЕНИЕ Б …..…………………………...…….. 26

ПРИЛОЖЕНИЕ В ……………...……………………… 27

БИБЛИОГРАФИЧЕСКИЙ СПИСОК ……...….……... 27

ПРОГРАММА, КОНТРОЛЬНЫЕ ЗАДАНИЯ

И МЕТОДИЧЕСКИЕ УКАЗАНИЯ

по дисциплине «Теория скрытности»

по направлению 11.03.01 «Радиотехника»,

профилю «Радиотехнические средства передачи,

приема и обработки сигналов»

для студентов заочной формы обучения

Составитель: Литвиненко Владимир Петрович

В авторской редакции

ЛР № 066815 от 25.08.99. Подписано к печати 22.12.2015.

Формат 60x84/16. Бумага для множительных аппаратов.

Усл. печ. л. 1,3. Уч.-изд. л. 1,2. Тираж 50 экз. «С»

Зак. №

ГОУВПО «Воронежский государственный технический университет»

394026 Воронеж, Московский просп. 14

ПРОГРАММА, КОНТРОЛЬНЫЕ ЗАДАНИЯ

И МЕТОДИЧЕСКИЕ УКАЗАНИЯ

по дисциплине «Теория скрытности»

по направлению 11.03.01 «Радиотехника»,

профилю «Радиотехнические средства передачи,

приема и обработки сигналов»

для студентов заочной формы обучения

Воронеж 2016

Составитель канд. техн. наук В.П. Литвиненко

УДК 621.391

Программа, контрольные задания и методические указания по дисциплине «Теория скрытности» для подготовки бакалавров, обучающихся по направлению 11.03.01 «Радиотехника», профилю «Радиотехнические средства передачи, приема и обработки сигналов»заочной формы обучения / ФГБОУ ВПО «Воронежский государственный технический университет»; сост. В.П. Литвиненко. Воронеж, 2016. 28 с.

Приведены программа, контрольные задания и методические указания к контрольной работе и лабораторным занятиям по дисциплине «Теория скрытности».

Контрольная и лабораторные работы выполняются с помощью современной вычислительной техники на основе разработанной на кафедре радиотехники программы Poisk.exe. Предусматривается использование пакета программ MathCAD и других систем программирования.

Методические указания предназначены для студентов третьего курса.

Табл. 2. Ил. 3. Библиогр.: 5 назв.

Рецензент д-р. техн. наук, проф. А.Б. Токарев

Ответственный за выпуск зав. кафедрой канд. техн. наук, проф. Б.В. Матвеев

Печатается по решению редакционно-издательского совета Воронежского государственного технического университета

Ó ФГБОУ ВПО «Воронежский государственный технический университет», 2016

ВВЕДЕНИЕ

Дисциплина «Теория скрытности» введена решением Совета ВГТУ в рамках профиля «Радиотехнические средства передачи, приема и обработки сигналов»по направлению 11.03.01 «Радиотехника».

Целью дисциплины «Теория скрытности» является изучение методов оценки и анализа скрытности и защищенности от радиоразведки радиосигналов и систем радиосвязи, исследование алгоритмов поиска состояния объекта и методов их оптимизации.

Задачи дисциплины состоят в освоении методов анализа разведывательной защищенности систем связи, проектирования эффективных поисковых процедур и их оптимизации в различных технических задачах разведки, диагностики, поиска сигналов и синхронизации.

СОДЕРЖАНИЕ РАБОЧЕЙ ПРОГРАММЫ

ПРЕПОДАВАНИЯ ДИСЦИПЛИНЫ

Требования к уровню освоения содержания

дисциплины

В результате изучения дисциплины формируются следующие компетенции обучающегося:

- ОПК‑2 - способность выявлять естественнонаучную сущность проблем, возникающих в ходе профессиональной деятельности, привлекать для решения соответствующий физико-математический аппарат;

- ПК-1 - способность выполнять математическое моделирование объектов и процессов по типовым методикам, в том числе с использованием стандартных пакетов прикладных программ;

- ПВК‑1 - способность оценивать скрытность сигналов и систем радиосвязи, энергетическую защищенность радиолиний, проводить вероятностные расчеты различных видов скрытности.

Студент должен знать методы оценки скрытности, алгоритмы поиска состояния объекта и методы их оптимизации, влияние на скрытность помех и маскирующих сигналов, характеристики скрытности различных сигналов и систем радиосвязи. Студент должен уметь проводить расчеты скрытности состояния объекта в различных условиях, проектировать оптимальные поисковые процедуры, выполнять сравнительный анализ скрытности сигналов. Студент должен приобрести навыки проведения расчетов скрытности и моделирования поисковых процедур, в том числе и с использованием со