Построение теоретического ряда и вычисление степени его совпадения с практическим распределением
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
ВОРОНЕЖСКАЯ ГОСУДАРСТВЕННАЯ ЛЕСОТЕХНИЧЕСКАЯ АКАДЕМИЯ
КАФЕДРА ЛЕСОВОДСТВА, ЛЕСНОЙ ТАКСАЦИИ И ЛЕСОУСТРОЙСТВА
РАБОЧАЯ ТЕТРАДЬ
Для выполнения лабораторных работ по дисциплине:
«Математические методы в лесном хозяйстве»
Исполнитель студент (ка) II курса______группы
______________________________
Руководитель ______________________________
Работа сдана на кафедру « »_________2011 г.
Воронеж
Условные обозначения
Vmin – минимальная варианта ряда
Vmax – максимальная варианта ряда
PP – размер ряда
Kk – количество классов
λ – величина интервала
n – частота
W – среднее значение класса
M –среднее значение признака
α – отклонение от среднего значения
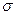– основное среднеквадратическое отклонение
C – коэффициент изменчивости (варьирования)
PM – показатель точности исследования
Me – медиана
Mo – мода
mM – основная ошибка среднего значения
mc – ошибка коэффициента изменчивости
m 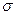– ошибка основного отклонения
tM – показатель достоверности среднего значения
A – условное начало
a –отклонение от условного начала, выраженное в долях интервала
υ1….υ4 – начальные моменты
μ1….μ4 – центральные моменты
r1….r4 –основные моменты
К – мера асимметрии
i – мера крутости
N – общее число наблюдений
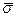– неполное среднеквадратическое отклонение
nmax – максимальная частота
nтеор. – теоретическая частота
γ – число классов (с учетом их объединения)
U – число занятых связей
f – число степеней свободы
χ2 – критерий согласия Пирсона
Yср – условно среднее значение
r – коэффициент корреляции
mr – ошибка коэффициента корреляции
tr – показатель достоверности коэффициента корреляции
tst – стандартное значение критерия Стьюдента
η – корреляционное отношение
mη – ошибка корреляционного отношения
tη – показатель достоверности корреляционного отношения
Z – мера линейности
mz – ошибка меры линейности
tz – показатель Блекмана
Dф – дисперсия факториальная
Dс – дисперсия случайная
Dо – дисперсия общая
Mr – групповые средние
S – средний квадрат суммы всех вариант дисперсионного комплекса
∑S – сумма средних квадратов суммы вариант по градациям комплекса
∑V2 – сумма квадратов всех вариант комплекса
η2 – сила влияния действующего фактора
mη – ошибка силы влияния
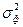– факториальная варианса
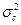– случайная варианса
F – достоверность силы влияния
Fst – стандартное значение критерия Фишера
d – разность между средней по контролю и групповыми средними
md – ошибка разности
ПОСТРОЕНИЕ ВАРИАЦИОННОГО РЯДА И ЕГО ГРАФИЧЕСКОЕ ИЗОБРАЖЕНИЕ
Характеристика наблюдения:
1. Изучаемый признак _____________________________________________________________
2. Число наблюдений (N)___________________________________________________________
Данные наблюдений
Вспомогательные данные для построения вариационного ряда
| 1. Минимальная варианта (Vmin) | Расчет величины интервала |
| 2. Максимальная варианта (Vmax) | |
| 3. Размер ряда | |
| 4. Количество классов | |
| расчетное фактическое | |
| 5. Величина интервала | |
| расчетная фактическая | |
| 6. Среднее значение начального класса |
Построение вариационного ряда
| Границы классов | ||||||||||||
| Средние значения классов (W) | ||||||||||||
| Частоты (точковка) | ||||||||||||
| Частоты (n) | ||||||||||||
| Частости, % | ||||||||||||
| Накопление частоты | ||||||||||||
| Накопление частости |
Графическое изображение вариационного ряда
Y
Х
полигон распределения ________ гистограмма __________ огива_________
Масштабы:
| Горизонтальный в 1 см – | Вертикальный для частот: в 1 см вариант |
| для накопленных частот: в 1 см – вариант |
ВЫЧИСЛЕНИЕ ПОКАЗАТЕЛЕЙ ВАРИАЦИОННОГО РЯДА
Изучаемый признак
1. Вычисление показателей вариационного ряда по исходным формулам
| W | n | W ∙ n | Mср | α= (W-M) | α ∙ n | α2 | α2 n |
где: W – среднее значение класса;
M – среднее значение признака.
ХОД ВЫЧИСЛЕНИЙ
| 1. Среднее значение признака | 2. Основное отклонение |
| 3. Основная ошибка среднего значения | 4. Коэффициент изменчивости |
| 5. Показатель точности исследования | 6. Показатель достоверности среднего значения |
| 7. Медиана | 8. Мода |
| 9. Ошибка основного отклонения | 10. Ошибка меры изменчивости |
II. Вычисление моментов
1. Вычисление начальных моментов
а) Вычисление начальных моментов способом произведений
| W | n | А | а* | аn | а2 | а2n | а3 | а3n | а4 | а4n |
* 
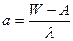, где:
W – среднее значение класса:
А – условная средняя величина (произвольное начало)
1-й момент (υ1)________________________________2-й момент (υ2)___________________
__________________________________________________________________________________________________________________________________________________________
3-й момент (υ3)________________________________4-й момент (υ4)___________________
__________________________________________________________________________________________________________________________________________________________
б) Вычисление начальных моментов способом сумм
| W | n | S1 | S2 | S3 | S4 | Ход вычислений 1-й момент (υ1)________________________ _____________________________________ 2-й момент (υ2)________________________ _____________________________________ 3-й момент (υ3)________________________ _____________________________________ 4-й момент (υ4)________________________ ______________________________________ |
| – S | ||||||
| + S | ||||||
| d | ||||||
| S |
2. Вычисление центральных моментов
1-й момент (μ1)________________________________________________________________
_____________________________________________________________________________
2-й момент (μ2)________________________________________________________________
_____________________________________________________________________________
3-й момент (μ3)________________________________________________________________
_____________________________________________________________________________
4-й момент (μ4)________________________________________________________________
_____________________________________________________________________________
Вычисление основных моментов
1-й момент (r1)________________________________________________________________
2-й момент (r2)________________________________________________________________
3-й момент (r3)_________________________________________________________________
4-й момент (r4)_________________________________________________________________
III. Вычисление показателей вариационного ряда с использованием значений моментов
1. Среднее значение признака____________________________________________________
_____________________________________________________________________________
2. Основное отклонение_________________________________________________________
_____________________________________________________________________________
3. Мера асимметрии (косости)____________________________________________________
Оценка асимметрии:____________________________________________________________
4. Мера крутости_______________________________________________________________
Оценка крутости_______________________________________________________________
Приложение 3
Определение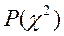
  | |||||||||||
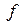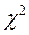| 0,6065 | 0,8013 | 0,9098 | 0,9626 | 0,9856 | 0,9948 | 0,9982 | 0,9994 | 0,9994 | 1,0 | 1,0 | |
| 0,9985 | 0,9994 | ||||||||||
| – | – | – | – | – | – |
Приложение 4
Стандартные значения критерия td для трех
степеней вероятности (по Стьюденту)
| Число степеней свободы υ | Вероятность (Р) | ||
| 0,95 | 0,99 | 0,999 | |
| 12,7 | 63,7 | 637,0 | |
| 4,3 | 9,9 | 31,6 | |
| 3,2 | 5,8 | 12,9 | |
| 2,8 | 4,6 | 8,6 | |
| 2,6 | 4,0 | 6,9 | |
| 2,4 | 3,7 | 6,0 | |
| 2,4 | 3,5 | 5,3 | |
| 2,3 | 3,4 | 5,0 | |
| 2,3 | 3,3 | 4,8 | |
| 2,2 | 3,2 | 4,6 | |
| 2,2 | 3,1 | 4,4 | |
| 2,2 | 3,1 | 4,3 | |
| 2,2 | 3,0 | 4,1 | |
| 14-15 | 2,1 | 3,0 | 4,1 |
| 16-17 | 2,1 | 2,9 | 4,0 |
| 18-20 | 2,1 | 2,9 | 3,9 |
| 21-24 | 2,1 | 2,8 | 3,8 |
| 25-28 | 2,1 | 2,8 | 3,7 |
| 29-30 | 2,0 | 2,8 | 3,7 |
| 31-34 | 2,0 | 2,7 | 3,7 |
| 35-42 | 2,0 | 2,7 | 3,5 |
| 43-62 | 2,0 | 2,7 | 3,5 |
| 63-175 | 2,0 | 2,6 | 3,4 |
| 176 и более | 2,0 | 2,6 | 3,3 |
Приложение 5
Стандартные значения критерия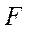 
для уровня вергоятности 0,95 (критерий Фишера)
| Число степеней свободы f2 для меньшей дисперсии | Число степеней свободы f1 для большей дисперсии, которая берется числителем | ||||||||||||
| 18,5 | 19,2 | 19,2 | 19,3 | 19,3 | 19,4 | 19,4 | 19,4 | 19,4 | 19,4 | 19,4 | 19,5 | 19,5 | |
| 10,1 | 9,6 | 9,3 | 9,1 | 9,0 | 8,9 | 8,9 | 8,8 | 8,8 | 8,8 | 8,7 | 8,6 | 8,5 | |
| 7,7 | 6,9 | 6,6 | 6,4 | 6,3 | 6,2 | 6,1 | 6,0 | 6,0 | 6,0 | 5,9 | 5,8 | 5,6 | |
| 6,6 | 5,8 | 5,4 | 5,2 | 5,1 | 5,0 | 4,9 | 4,8 | 4,8 | 4,7 | 4,7 | 4,5 | 4,4 | |
| 6,0 | 5,1 | 4,8 | 4,5 | 4,4 | 4,3 | 4,2 | 4,2 | 4,1 | 4,1 | 4,0 | 3,8 | 3,7 | |
| 5,6 | 4,7 | 4,4 | 4,1 | 4,0 | 3,9 | 3,8 | 3,7 | 3,7 | 3,6 | 3,6 | 3,4 | 3,2 | |
| 5,3 | 4,5 | 4,1 | 3,8 | 3,7 | 3,6 | 3,5 | 3,4 | 3,4 | 3,3 | 3,3 | 3,1 | 2,9 | |
| 5,1 | 4,3 | 3,9 | 3,6 | 3,5 | 3,4 | 3,3 | 3,2 | 3,2 | 3,1 | 3,1 | 2,9 | 2,7 | |
| 5,0 | 4,1 | 3,7 | 3,5 | 3,3 | 3,2 | 3,1 | 3,1 | 3,0 | 3,0 | 2,9 | 2,7 | 2,5 | |
| 4,8 | 4,0 | 3,6 | 3,4 | 3,2 | 3,1 | 3,0 | 3,0 | 2,9 | 2,9 | 2,8 | 2,6 | 2,4 | |
| 4,8 | 3,9 | 3,5 | 3,3 | 3,1 | 3,0 | 2,9 | 2,8 | 2,8 | 2,8 | 2,7 | 2,5 | 2,3 | |
| 4,7 | 3,8 | 3,4 | 3,2 | 3,0 | 2,9 | 2,8 | 2,8 | 2,7 | 2,7 | 2,6 | 2,4 | 2,2 | |
| 4,6 | 3,7 | 3,3 | 3,1 | 3,0 | 2,9 | 2,8 | 2,7 | 2,6 | 2,6 | 2,5 | 2,3 | 2,1 | |
| 4,5 | 3,7 | 3,3 | 3,1 | 2,9 | 2,8 | 2,7 | 2,6 | 2,6 | 2,6 | 2,5 | 2,3 | 2,1 | |
| 4,5 | 3,6 | 3,2 | 3,0 | 2,9 | 2,7 | 2,7 | 2,6 | 2,6 | 2,5 | 2,4 | 2,2 | 2,0 | |
| 4,5 | 3,6 | 3,2 | 3,0 | 2,8 | 2,7 | 2,6 | 2,6 | 2,5 | 2,4 | 2,4 | 2,2 | 2,0 | |
| 4,4 | 3,6 | 3,2 | 2,9 | 2,8 | 2,7 | 2,6 | 2,5 | 2,4 | 2,4 | 2,3 | 2,1 | 1,9 | |
| 4,4 | 3,5 | 3,1 | 2,9 | 2,7 | 2,6 | 2,6 | 2,5 | 2,4 | 2,4 | 2,3 | 2,1 | 1,9 | |
| 4,4 | 3,5 | 3,1 | 2,9 | 2,7 | 2,6 | 2,5 | 2,4 | 2,4 | 2,4 | 2,3 | 2,1 | 1,8 | |
| 4,3 | 3,4 | 3,1 | 2,8 | 2,7 | 2,6 | 2,5 | 2,4 | 2,4 | 2,3 | 2,2 | 2,0 | 1,8 | |
| 4,3 | 3,4 | 3,0 | 2,8 | 2,6 | 2,5 | 2,4 | 2,4 | 2,3 | 2,3 | 2,2 | 2,0 | 1,7 |
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
ВОРОНЕЖСКАЯ ГОСУДАРСТВЕННАЯ ЛЕСОТЕХНИЧЕСКАЯ АКАДЕМИЯ
КАФЕДРА ЛЕСОВОДСТВА, ЛЕСНОЙ ТАКСАЦИИ И ЛЕСОУСТРОЙСТВА
РАБОЧАЯ ТЕТРАДЬ
Для выполнения лабораторных работ по дисциплине:
«Математические методы в лесном хозяйстве»
Исполнитель студент (ка) II курса______группы
______________________________
Руководитель ______________________________
Работа сдана на кафедру « »_________2011 г.
Воронеж
Условные обозначения
Vmin – минимальная варианта ряда
Vmax – максимальная варианта ряда
PP – размер ряда
Kk – количество классов
λ – величина интервала
n – частота
W – среднее значение класса
M –среднее значение признака
α – отклонение от среднего значения
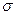– основное среднеквадратическое отклонение
C – коэффициент изменчивости (варьирования)
PM – показатель точности исследования
Me – медиана
Mo – мода
mM – основная ошибка среднего значения
mc – ошибка коэффициента изменчивости
m 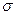– ошибка основного отклонения
tM – показатель достоверности среднего значения
A – условное начало
a –отклонение от условного начала, выраженное в долях интервала
υ1….υ4 – начальные моменты
μ1….μ4 – центральные моменты
r1….r4 –основные моменты
К – мера асимметрии
i – мера крутости
N – общее число наблюдений
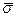– неполное среднеквадратическое отклонение
nmax – максимальная частота
nтеор. – теоретическая частота
γ – число классов (с учетом их объединения)
U – число занятых связей
f – число степеней свободы
χ2 – критерий согласия Пирсона
Yср – условно среднее значение
r – коэффициент корреляции
mr – ошибка коэффициента корреляции
tr – показатель достоверности коэффициента корреляции
tst – стандартное значение критерия Стьюдента
η – корреляционное отношение
mη – ошибка корреляционного отношения
tη – показатель достоверности корреляционного отношения
Z – мера линейности
mz – ошибка меры линейности
tz – показатель Блекмана
Dф – дисперсия факториальная
Dс – дисперсия случайная
Dо – дисперсия общая
Mr – групповые средние
S – средний квадрат суммы всех вариант дисперсионного комплекса
∑S – сумма средних квадратов суммы вариант по градациям комплекса
∑V2 – сумма квадратов всех вариант комплекса
η2 – сила влияния действующего фактора
mη – ошибка силы влияния
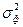– факториальная варианса
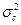– случайная варианса
F – достоверность силы влияния
Fst – стандартное значение критерия Фишера
d – разность между средней по контролю и групповыми средними
md – ошибка разности
ПОСТРОЕНИЕ ВАРИАЦИОННОГО РЯДА И ЕГО ГРАФИЧЕСКОЕ ИЗОБРАЖЕНИЕ
Характеристика наблюдения:
1. Изучаемый признак _____________________________________________________________
2. Число наблюдений (N)___________________________________________________________
Данные наблюдений
Вспомогательные данные для построения вариационного ряда
| 1. Минимальная варианта (Vmin) | Расчет величины интервала |
| 2. Максимальная варианта (Vmax) | |
| 3. Размер ряда | |
| 4. Количество классов | |
| расчетное фактическое | |
| 5. Величина интервала | |
| расчетная фактическая | |
| 6. Среднее значение начального класса |
Построение вариационного ряда
| Границы классов | ||||||||||||
| Средние значения классов (W) | ||||||||||||
| Частоты (точковка) | ||||||||||||
| Частоты (n) | ||||||||||||
| Частости, % | ||||||||||||
| Накопление частоты | ||||||||||||
| Накопление частости |
Графическое изображение вариационного ряда
Y
Х
полигон распределения ________ гистограмма __________ огива_________
Масштабы:
| Горизонтальный в 1 см – | Вертикальный для частот: в 1 см вариант |
| для накопленных частот: в 1 см – вариант |
ВЫЧИСЛЕНИЕ ПОКАЗАТЕЛЕЙ ВАРИАЦИОННОГО РЯДА
Изучаемый признак
1. Вычисление показателей вариационного ряда по исходным формулам
| W | n | W ∙ n | Mср | α= (W-M) | α ∙ n | α2 | α2 n |
где: W – среднее значение класса;
M – среднее значение признака.
ХОД ВЫЧИСЛЕНИЙ
| 1. Среднее значение признака | 2. Основное отклонение |
| 3. Основная ошибка среднего значения | 4. Коэффициент изменчивости |
| 5. Показатель точности исследования | 6. Показатель достоверности среднего значения |
| 7. Медиана | 8. Мода |
| 9. Ошибка основного отклонения | 10. Ошибка меры изменчивости |
II. Вычисление моментов
1. Вычисление начальных моментов
а) Вычисление начальных моментов способом произведений
| W | n | А | а* | аn | а2 | а2n | а3 | а3n | а4 | а4n |
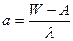* , где:
W – среднее значение класса:
А – условная средняя величина (произвольное начало)
1-й момент (υ1)________________________________2-й момент (υ2)___________________
__________________________________________________________________________________________________________________________________________________________
3-й момент (υ3)________________________________4-й момент (υ4)___________________
__________________________________________________________________________________________________________________________________________________________
б) Вычисление начальных моментов способом сумм
| W | n | S1 | S2 | S3 | S4 | Ход вычислений 1-й момент (υ1)________________________ _____________________________________ 2-й момент (υ2)________________________ _____________________________________ 3-й момент (υ3)________________________ _____________________________________ 4-й момент (υ4)________________________ ______________________________________ |
| – S | ||||||
| + S | ||||||
| d | ||||||
| S |
2. Вычисление центральных моментов
1-й момент (μ1)________________________________________________________________
_____________________________________________________________________________
2-й момент (μ2)________________________________________________________________
_____________________________________________________________________________
3-й момент (μ3)________________________________________________________________
_____________________________________________________________________________
4-й момент (μ4)________________________________________________________________
_____________________________________________________________________________
Вычисление основных моментов
1-й момент (r1)________________________________________________________________
2-й момент (r2)________________________________________________________________
3-й момент (r3)_________________________________________________________________
4-й момент (r4)_________________________________________________________________
III. Вычисление показателей вариационного ряда с использованием значений моментов
1. Среднее значение признака____________________________________________________
_____________________________________________________________________________
2. Основное отклонение_________________________________________________________
_____________________________________________________________________________
3. Мера асимметрии (косости)____________________________________________________
Оценка асимметрии:____________________________________________________________
4. Мера крутости_______________________________________________________________
Оценка крутости_______________________________________________________________
ПОСТРОЕНИЕ ТЕОРЕТИЧЕСКОГО РЯДА И ВЫЧИСЛЕНИЕ СТЕПЕНИ ЕГО СОВПАДЕНИЯ С ПРАКТИЧЕСКИМ РАСПРЕДЕЛЕНИЕМ
1. Выравнивание практического ряда по нормальному закону с помощью таблицы ординат нормальной кривой
ИСХОДНЫЕ ДАННЫЕ
Изучаемый признак____________________________________________________________
Среднее значение признака (М)__________________________________________________
Полное среднее квадратическое отклонение (именованное) (σ) _______________________
Число наблюдений (N)__________________________________________________________
Величина интервала (λ)_________________________________________________________
ПОДГОТОВИТЕЛЬНЫЕ РАБОТЫ
Минимальная варианта нормального ряда (Wmin)____________________________________
Максимальная варианта нормального ряда (Wmax)___________________________________
Неполное среднее квадратическое отклонение (в условных единицах) ( )______________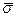
Максимальная частота (n макс)____________________________________________________