Свойства функции распределения.

1. .

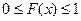2. Функция распределения случайной величины есть неубывающая функция на всей числовой оси.

3. , .

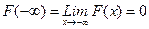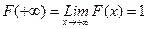4. Р(х₁ 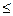Х<x₂)=F(x₂)-F(x₁). (4)

Пример: 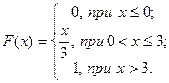Найти вероятность того, что случайная величина Х примет значение в интервале [2; 5).

Решение:По формулеР(х₁ 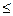Х<x₂)=F(x₂)-F(x₁). (4)

Р(2 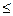Х<5)=F(5)-F(2)=1-2/3=1/3. (4).

Ответ : 1/3.

Математические операции над случайными величинами.

Определение: Случайные величины называются независимыми, если закон распределения одной из них не зависит от того, какое значение принимает другая случайная величина. В противном случае случайные величины называются зависимыми.

Пример:Суммы выигрыша в двух различных лотереях – независимые случайные величины так как при любом выигрыше в первой лотерее, закон распределения выигрышей по второй лотерее не изменится.

Определим математические операции над дискретными случайными величинами.

Пусть даны две случайные величины: Х и Y

xi	х1	х2	х3	…..	xn
pi	p1	p2	p3	…..	pn

yj	y1	y2	y3	…..	ym
pj	p1	p2	p3	…..	pm

1. Произведением kX случайной величины Х на постоянную величину k называется случайная величина, которая принимает значения kx_i с теми же вероятностями p_i (i=1, …, n).
2. Cтепенью m случайной величины Х называется случайная величина Х^m, которая принимает значения x_i^m с теми же вероятностями p_i (i=1, …, n).

Замечание: так как в ряде случаев одни и те же значения x_i^m могут получаться одними и теми же способами при различных x_i , то вероятности таких повторяющихся значений находятся сложением исходных вероятностей.

Пример:Дана случайная величина Х:

xi	-3	-2
pi	0,1	0,2	0,05	0,3	0,35

Найти закон распределения случайных величин 5Х и Х².

Решение:Закон распределения случайной величины 5X.

5xi	-15	-10
pi	0,1	0,2	0,05	0,3	0,35

Случайная величина Х² примет значения (-3)²=9; (-2)²=4; (0)²=0; 1²=1 и 2²=4.

Значение Х=4 получили при значении х=-2 с вероятностью 0,2 и при значении х=2 с вероятностью 0,45. Тогда Р(Х²=4)=0,2+0,35=0,55.

Закон распределения случайной величины X².

Xi2
pi	0,05	0,3	0,55	0,1

3. Суммой (разностью или произведением) случайных величин Х и Y называется случайная величина, которая принимает все возможные значения вида х_i+y_j (х_i-y_j или х_iy_j), где i=1, 2,…, n, j=1, …, m с вероятностями p_ij=Р 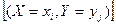. Если случайные величины независимы, то по теореме умножения вероятностей

p_ij=Р 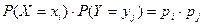(5)

Замечание: так как в ряде случаев одни и те же значения х_i+y_j (х_i-y_j или х_iy_j), могут получаться одними и теми же способами при различных x_i ,y_j то вероятности таких повторяющихся значений находятся сложением исходных вероятностей p_i или p_ij .

Пример:Даны законы распределения двух случайных величин Х и Y:

xi	-2
pi	0,2	0,1	0,3	0,4

yi	-2
pi	0,1	0,2	0,1	0,6

Найти закон распределения случайных величин а )Z=X+Y; б)U=XY.

Решение:Составим вспомогательную таблицу:

X+Y	yj	-2
xi	pi pj	0,1	0,2	0,1	0,6
-2	0,2	-4 0,02	-2 0,04	-1 0,02	2 0,12
	0,1	-2 0,01	0 0,02	1 0,01	4 0,06
	0,3	-1 0,03	1 0,06	2 0,03	5 0,18
	0,4	0 0,04	2 0,08	3 0,04	6 0,24

Таблица заполняется следующим образом: в каждой клетке таблицы в левом углу находится значение разности х_i-y_j , а в правом углу – вероятности этих значений, полученные в результате перемножения вероятностей p_i и p_j .

Так как среди 16 значений таблицы находятся повторяющиеся, то соответствующие вероятности их складываем по теореме сложения вероятностей. Например, значение

Z=X+Y=0 может быть получено, когда X=2, Y=-2 с вероятностью 0,04; Х=0,Y=0 с вероятностью 0,02, поэтому Р(Z=0)=0,04+0,02=0,06 и т.д.

zi	-4	-2	-1
pi	0,02	0,05	0,05	0,06	0,07	0,23	0,04	0,06	0,18	0,24

Убедимся, что условие 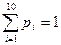выполнено.

Б) аналогично составляем таблицу для U=XY

XY	yj	-2
xi	pi pj	0,1	0,2	0,1	0,6
-2	0,2	4 0,02	0 0,04	-2 0,02	-8 0,12
	0,1	0 0,01	0 0,02	0 0,01	0 0,06
	0,3	-2 0,03	0 0,06	1 0,03	4 0,18
	0,4	-4 0,04	0 0,08	2 0,04	8 0,24

ui	-8	-4	-2
pi	0,12	0,04	0,05	0,28	0,03	0,07	0,2	0,24