Относительное линейное отклонение

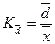
3.на основе среднего квадратического отклонения

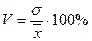- коэффициент вариации

Как правило измеряется в % и является наиболее используемым в практическом анализе. Характеризует относительную меру изменчивости. По его величине делается вывод об однородности или неоднородности изучаемой совокупности.

Если V ≤ 33 % , то совокупность признается однородной.

Коэффициент вариации как относительная мера изменчивости используется для сравнения степени однородности совокупности по разноименным признакам, а также для сравнения степени вариации по разным совокупностям.

10. Правило сложения дисперсий

Общая дисперсия – сумма межгрупповой и внутригрупповой дисперсий.

Таблица

Производительность труда рабочих (деталей в смену)
Рабочие, имеющие специальное техническое образование	Не имеющие специального технического образования

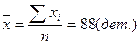
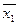= 95 (дет.) , 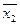= 81 (дет.)

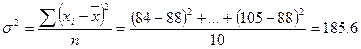
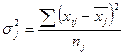
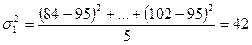
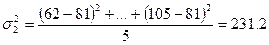
На основе внутригрупповых дисперсий рассчитана средняя дисперсия.

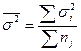
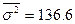
Межгрупповая дисперсия:

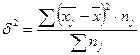
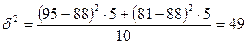
Общая дисперсия:

σ² = δ² + σ²

185,6 = 49 + 136,6

Общая дисперсия – дисперсия, характеризующая вариацию признака под влиянием всех факторов.

Межгрупповая дисперсия характеризует вариацию анализируемого признака, обусловленную группировочным признаком.

Внутригрупповая дисперсия оценивает вариацию признака, обусловленную всеми остальными факторами, за исключением группировочного.

Поэтому общая дисперсия равна сумме межгрупповой и внутригрупповой дисперсий.

В условиях собственно-случайной выборки в формуле средней ошибки выборки используется общая дисперсия

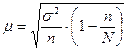
При стратифицированной выборке для расчета ошибки репрезентативности используется внутригрупповая дисперсия.

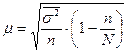
Серийная (гнездовая) выборка. Используется межгрупповая дисперсия:

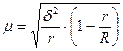, где

r - число серий в выборочной совокупности;

R - число серий в генеральной совокупности.

Максимальная ошибка выборки возникает при организации собственно-случайной выборки. Стратифицированный и серийный отборы, позволяющие сформировать выборку по структуре и закону распределения более близкую к генеральной совокупности, дают наименьшую величину ошибки.

11. Ряды распределения, вариационные ряды, правила их построения

Ряд распределения – распределение единиц совокупности по значениям того или иного признака в конкретны условиях места и времени.

Изучение рядов распределения по количественному признаку позволяет определить типический уровень признака в изучаемой совокупности, определить наличие выбросов и решить вопрос о необходимости их изучения, оценить степень разброса значений признака вокруг типического уровня, изучить структуру совокупности, описать форму распределения, а также подобрать теоретическое распределение, на основе которого можно прогнозировать поведение распределения изучаемого объекта.

Значение признака в рядах распределения называется вариантой (или вариантом).

Число единиц, обладающих тем или иным значением, называют частотой.

Ряды распределения могут быть представлены в табличной форме и графически.

Значение признака или варианты	Частота, fi	Частость, относительная частота, статистическая вероятность, f|i	Накопленные частоты, ∑ fi	Накопленные частости, ∑ f|i
x1	f1	f|1	f1	f|1
x2	f2	f|2	f1 + f2	f|1 + f|2
x3	f3	f|3	f1 + f2 + f3	f|1 + f|2 + f|3
…	…	…	…	…
xn	fn	f|n	f1 + f2 + … + fn	f|1 + f|2 + … + f|n

Первая графа содержит значение признака, если ряд строится по атрибутивному признаку или по дискретному количественному или интервалы значений признака, если ряд строится по непрерывному количественному признаку. В этом случае ряд называется интервальный вариационный ряд.

Вторая графа – частота. Количество единиц совокупности, обладающих данным значением признака.

Третья графа – частость, относительная частота, статистическая вероятность. Отношение числа каждой группы к сумме частот.

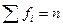
Четвертая графа – сумма накопленных частот. Кумулятивные частоты. Получаются путем последовательного суммирования частот по каждой группе.

Пятая графа – кумулятивные частости. Если сумма накопленных частот равна n, то сумма накопленных частостей равна 1.

,

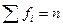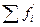
12. Графическое изображение рядов распределения.

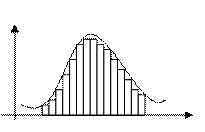
Полигон распределения строится в основном для рядов, построенных по дискретному признаку. Если полигон отображает интервальный вариационный ряд, то в качестве значений признака берется середина интервала.

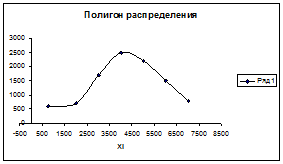
В качестве значений признака при построении графика берется середина каждого интервала. Открытые интервалы принимаются равными прочим интервалам.

Гистограмма.

Для интервального вариационного ряда. Гистограмма – столбиковая диаграмма. Основания столбиков – величина интервалов, их высота соответствует частотам.

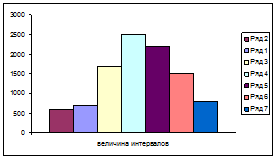
Графики рядов распределения могут строиться с использованием как частот, так и частостей распределения.

Кумулята строится с использованием накопленных частот или частостей.

Кумулята по накопленным относительным частотам:

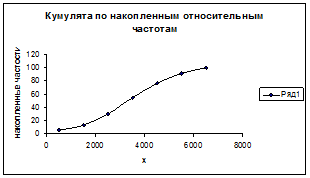
Нижней границей первого интервала соответствует нулевая частота, верхней – значение частоты или частости первого интервала.

Верхней границей второго интервала является накопленная частость и т.д.

На основе кумуляты можно дать ответ на вопрос «сколько процентов единиц совокупности имеют значение признака больше или меньше данного». То есть по кумуляте можно определить значение показателей структуры (в частности медианы и квартилей).

Кумулята дает возможность более подробно изучать структуру совокупности.

Графики ряда распределения могут быть построены без табличного представления анализируемого ряда распределения (с использованием пакета прикладных программ).

На практике построению графиков как правило предшествует табличное представление ряда распределения.

Построение ряда распределения начинают с ранжирования единиц совокупности по величине соответствующего признака. Построение ранжированного ряда позволяет увидеть наличие или отсутствие так называемых выбросов. Выбросы – значение признака, резко отличающееся в меньшую или большую сторону. Как правило, наличие таких значений связано с особыми условиями существования соответствующих единиц совокупности. Резко отличающиеся значения признака говорит о том, что данная единица не принадлежит данному распределению. Выбросы должны быть исключены из анализа общей закономерности распределения изучаемой совокупности. Однако на основе теоретического анализа необходимо обосновать причину их исключения, а также необходимость их самостоятельного детального исследования (последнее зависит от цели исследования).

Наличие выбросов следует отличать от бимодального или двухвершинного и полимодального распределения. Наличие двух и более вершин в распределении свидетельствует о неоднородности изучаемой совокупности, о присутствии в статистической совокупности двух или более самостоятельных групп (кластеров), которые, естественное, должны изучаться отдельно.

При построении ряда распределения следует стремиться к следующему:

1. не должно быть в распределении пустых и малонаполненных групп

2. наличие одновершинности в распределении. То есть по обе стороны от максимальной частоты должно наблюдаться закономерное убывание частот.

Путь к достижению одновершинности в распределении – постепенное сокращение числа выделяемых групп. Число групп должно быть не менее трех. Если сделав все шаги не удается получить одновершинность распределения, значит, имеет дело с бимодальным распределением. Значит, нужно отдельно изучать выделяющиеся кластеры.

13. Характеристики центра распределения.

Ряды распределения строятся по большим распределениям совокупности. При этом возникает необходимость получить характеристику всего набора данных с использованием одного обобщающего показателя. Прежде всего, таким показателем. Который характеризует совокупность в целом, отражает типический уровень признака в данной совокупности, является средняя арифметическая величина. Среднее рассчитывается на единицу совокупности, однако характеризует совокупность в целом.

По исходным данным средняя величина рассчитывается по средней арифметической простой; если по вариационному ряду – по средней арифметической взвешенной. В качестве весов – частоты, частости. Если среднее рассчитывается по интервальному ряду, в качестве индивидуальных значений признака используются середины интервала.

Мода (M₀) – наиболее часто встречающееся значение признаков совокупности.

Проблема расчета данного показателя связана с интервальным вариационным рядом.

Сначала находится модальный интервал (интервал, которому соответствует максимальная частота).

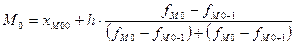, где

Х_М0о – нижняя граница модального интервала;

h – величина интервала;

f_{Mo – 1} - частота интервала, предшествующего модальному;

f_Mo – частота модального интервала;

f_{Mo + 1} - частота интервала, следующего за модальным.

Медиана (М_е) – значение признака у единицы, делящей ранжированный ряд пополам.

При определении медианы по ранжированному ряду без группировки

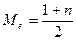
Если число единиц совокупности четное, то значение медианы определяется как среднее арифметическое двух центральных значений.

Если медиана рассчитывается по интервальному вариационному ряду, то сначала находят медианный интервал, а затем по формуле рассчитывается значение медианы.

Медианный интервал – это первый интервал, в который попадает 50% совокупности.

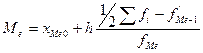, где

Х_Ме – нижняя граница медианного интервала;

f’_Me-1 – накопленная частота интервала, предшествующего медианному;

f_Me – частота медианного интервала;

∑ f_i - сумма накопленных частот.

Вопрос выбора показателя центра распределения зависит от типа характеристике, по которой построен ряд распределения, а также от целей исследования.

Если показатель количественный, то могут быть рассчитаны все показатели центра распределения (и средняя величина, и медиана). Тогда выбор показателя зависит от цели исследования и характера изучаемого распределения.

Если распределение соответствует нормальному распределению, то целесообразнее использовать среднюю величину.

Если в распределении наблюдается существенная асимметрия, то следует использовать либо моду, либо медиану, исходя из цели анализа.

При оценке распределений по атрибутивным признакам, средние значения рассчитаны быть не могут. Показатель моды может быть рассчитан по любому атрибутивному признаку, то есть измерен как по номинальной, так и по порядковой шкале.

14. Характеристики структуры распределения.

Медиана как значение показателя у единицы, делящей ранжированный ряд пополам, одновременно является характеристикой структуры распределения. Так как значение медианы характеризует структуру изучаемой совокупности, указывая, что 50% единиц имеют значение признака меньше медианного, и 50% - больше медианного.

Для более детальной характеристики структуры совокупности, используются такие показатели, как квартили, делящие ранжированный ряд на 4 равные части, децили – на 10 равных частей, перцентили – ни 100, и другие.

Возможность расчета тех или иных показателей определяется целью исследования и размером изучаемой совокупности.

Перечисленные показатели по интервальному вариационному ряду рассчитываются аналогично расчету медианы. То есть для расчета первого или нижнего квартиля сначала находят квартильный интервал, а затем значение первого квартиля.

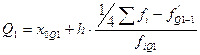- первый, нижний квартиль.

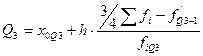- третий, верхний квартиль.

Значение Q₁ означает, что у 25% единиц совокупности значение показателя меньше квартильного, а у 75% - больше.

Значение Q₃: у 25% единиц совокупности значение больше данного.

Межквартильное расстояние Q₃ - Q₁ характеризует размах вариации в центре распределения. На этом интервале находится 50% единиц изучаемой совкупности.

15. Показатели формы распределения.

Как распределены единицы совокупности относительно центра.

К показателям формы распределения относятся:

- показатель асимметрии

- показатель эксцесса

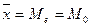- в нормальном распределении показатели центра распределения равны.

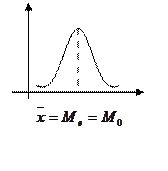Первый показатель асимметрии был предложен Пирсоном и строился на основе сравнения показателей центра распределения

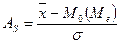- коэффициент асимметрии

Этот прием в статистике называется нормированием.

На основе этого показателя легко определяется вид асимметрии.

Если 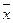> M₀ (M_e), то в распределении присутствует положительная правосторонняя асимметрия. Это означает, что чем больше значение признака, тем реже оно встречается в изучаемой совкупности.

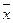< M₀ (M_e)- отрицательная левосторонняя асимметрия. Чем меньше значение признака, тем реже оно встречается в изучаемой совокупности.

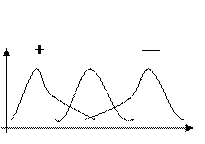
Показатель асимметрии Пирсона в большей степени оценивает асимметрию в центре распределения. Чтобы учесть асимметрию на концах распределения, используется показатель асимметрии, рассчитанный на основе центрального момента третьего порядка.

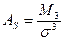
Момент распределения порядка k – среднее арифметическое отклонение k-ой степени индивидуальных значений от некоторой величины A.

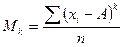
k – порядок момента, определяется степенью.

От того, что принимается в качестве A, отличают начальный, центральный и условный моменты.

A = 0 - начальный момент;

A = 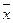- центральный момент;

A ≠ 0 ≠ 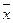- условный момент.

Формулы расчета моментов распределения

Порядок момента	Начальный момент	Центральный момент	Условный момент

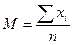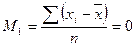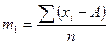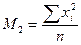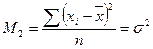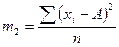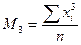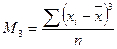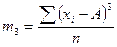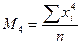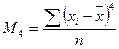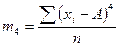Величина коэффициента асимметрии не имеет предела. Чтобы оценить статистическую значимость коэффициента асимметрии, то есть понять под влиянием каких факторов (случайных или не случайных) сформировано значение показателя. Рассчитывают стандартизованный коэффициент асимметрии.

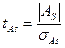- стандартизованный коэффициент асимметрии.

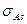- стандартная ошибка коэффициента асимметрии.

Коэффициент асимметрии берется по модулю, так как он может быть и положительным и отрицательным.

t_As ≥ 3 - асимметрия признается существенной, то есть сформированной под влиянием неслучайных факторов, и величина коэффициента асимметрии является статистически значимой.

t_As < 3 - асимметрия сформирована под влиянием случайных факторов. Асимметрия несущественная.

Коэффициент эксцесса.

Характеризует выпад вершины эмпирического распределения вверх или вниз относительно кривой нормального распределения. Так как нормальное распределение – это симметричное распределение, то коэффициент эксцесса имеет смысл рассчитывать при наличии несущественной асимметрии эмпирического распределения.

Коэффициент эксцесса может быть положительным, что будет означать выпад вершины вверх относительно вершины кривой нормального распределения, и отрицательным – вниз.

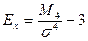, где

М₄ - центральный момент четвертого порядка.

Присутствие положительного эксцесса в изучаемом распределении означает, что в совокупности есть сформировавшееся ядро, то есть у большинства единиц совокупности близки значения изучаемой совокупности. Если в распределении присутствует отрицательный эксцесс, то в изучаемой совокупности нет сформировавшегося ядра, присутствует размытое гало.

Для оценки существенности эксцесса рассчитывается также стандартизованный эксцесс (куртозис):

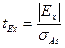
Если t_Ex ≥ 3, то эксцесс признается существенным, то есть сформированным под влиянием неслучайных факторов.

Если t_Ex < 3 , то эксцесс несуществененный, то есть сформированный под влиянием случайных факторов.

16. Задача сглаживания эмпирического распределения, выбор типа закономерности распределения.

При изучении эмпирических распределений выявляются определенные закономерности изменения частот при изменении значений признака. Эти закономерности называются закономерностями распределения. Теоретические распределения помимо графического представления могут быть представлены формально, то есть математическими формулами. Кривые теоретических распределений – это предел, к которому стремятся эмпирические распределения при условии неограниченного увеличения объема совокупности и сокращения величины группировочного интервала.

Гладкие непрерывные кривые теоретических распределений не могут быть получены по результатам эмпирических исследований, поскольку на практике, как правило, объем совокупности ограничен. Задача исследователя состоит в нахождении теоретического распределения, которое бы лучшим образом аппроксимировало изучаемое фактическое распределение. С этой целью осуществляется выравнивание фактического распределения. Выравнивание – замена фактических частот распределения теоретическими, рассчитанными по формуле соответствующего теоретического распределения по данным фактического распределения. Чаще всего осуществляют выравнивание по нормальному распределению, пытаясь оценить степень соответствия фактического или изучаемого распределения нормальному. Необходимость такой оценки связано с тем, что множество фактических распределений подчинено именно нормальному закону распределения, а также это связано с тем, что большинство методов статистического анализа ориентировано на закон нормального распределения.