Метод скорейшего спуска для решения систем нелинейных уравнений

Методом скорейшего спуска приближенно вычислить корни системы:

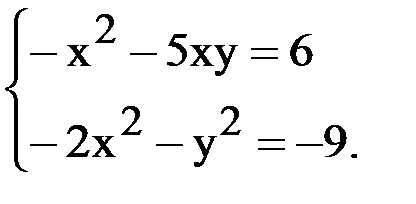
Решение.Пусть .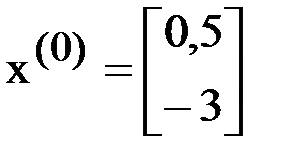

Здесь 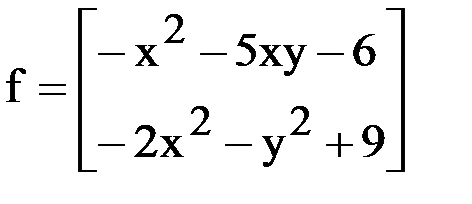и .

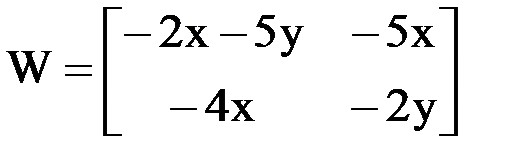Подставляя нулевое приближение, будем иметь

, , , , ,

.

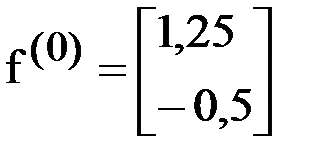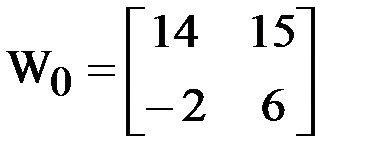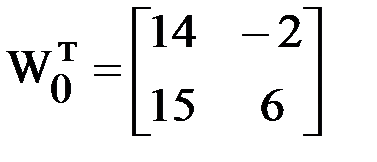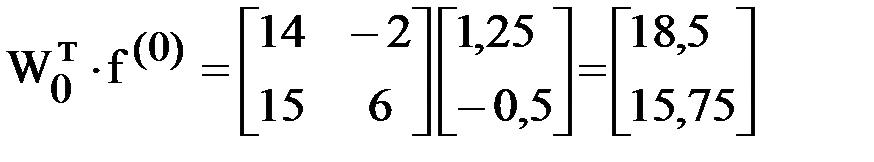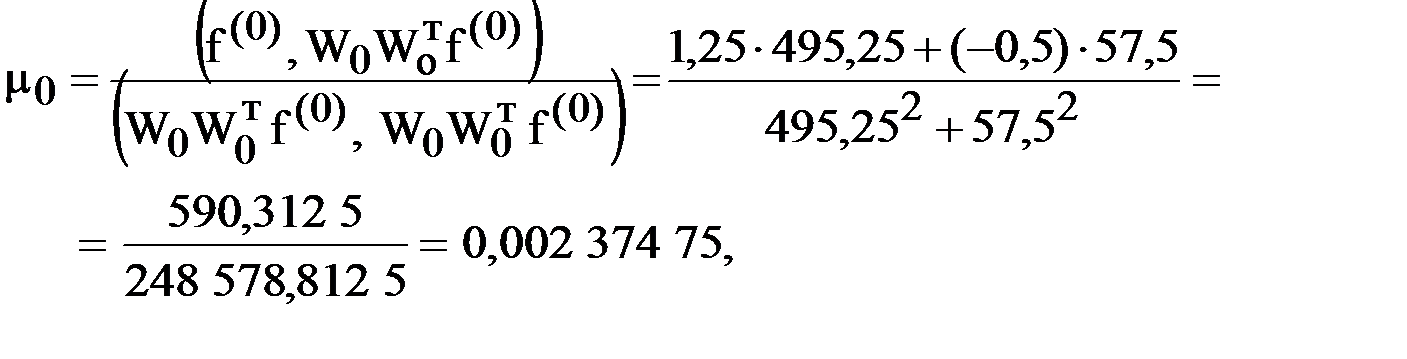
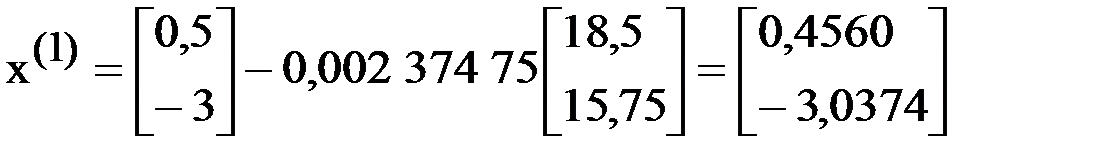Вычислим .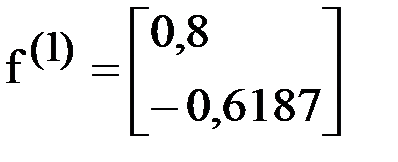

Аналогично найдем второе приближение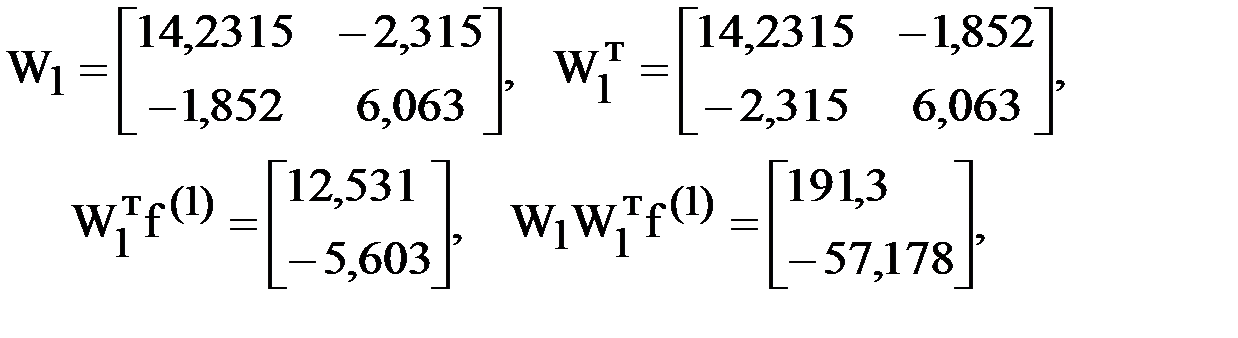

.

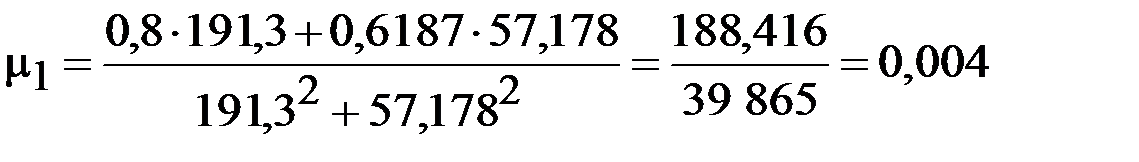Тогда .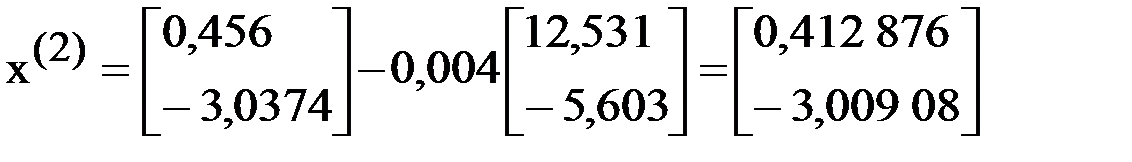

Для контроля вычислим невязку: 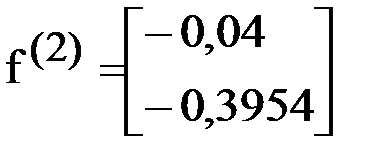и так далее.

Получаем решение системы: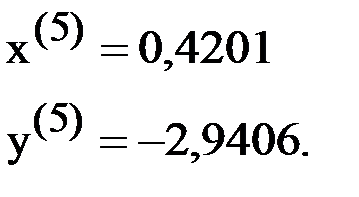

Метод скорейшего спуска для решения СЛАУ

Методом скорейшего случая решить систему уравнений:

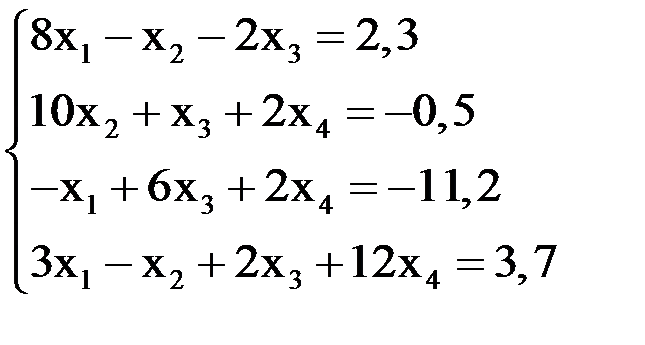
Решение.В качестве начального приближения выберем .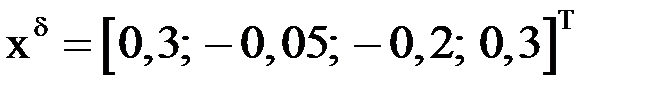

Тогда ,

,

.

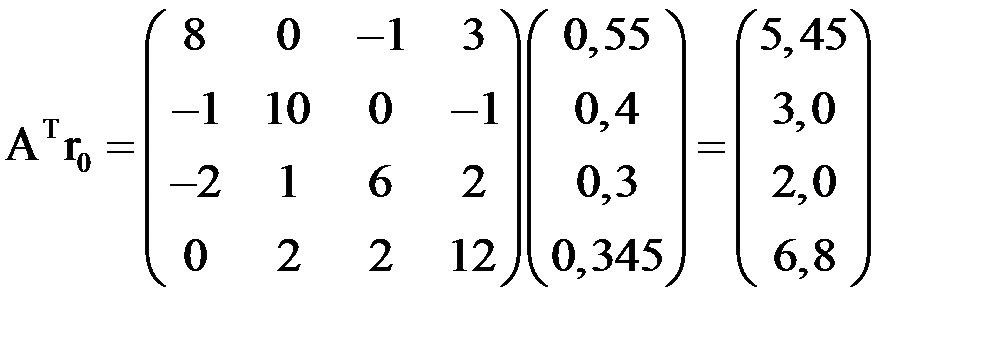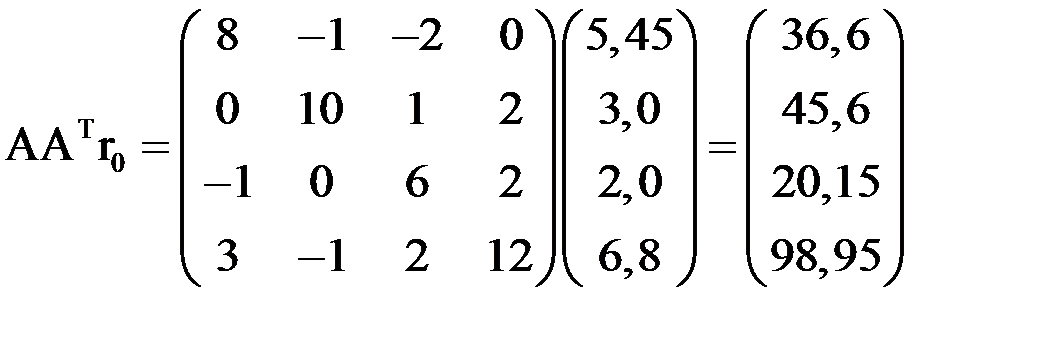Вычисляя коэффициент 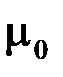, получим: .

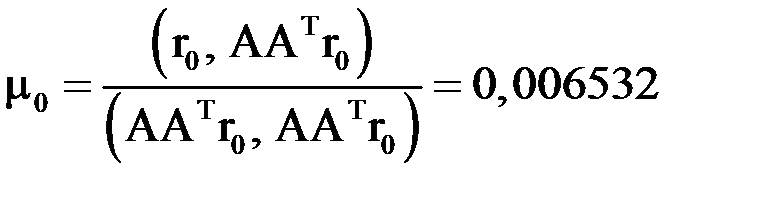Отсюда 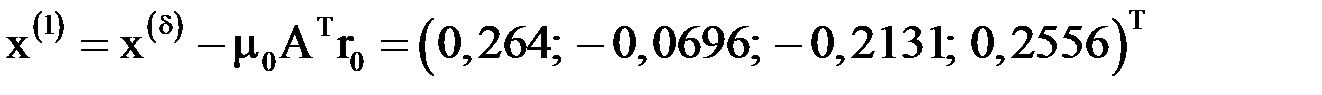, причем невязка 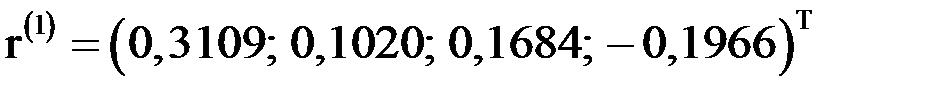. Аналогично вычисляя, получим: ;

;

;

.

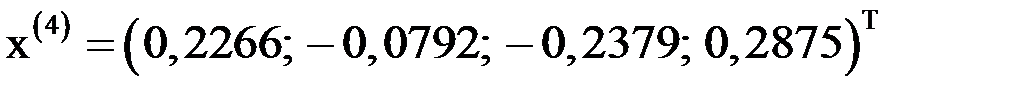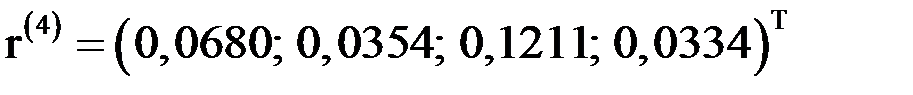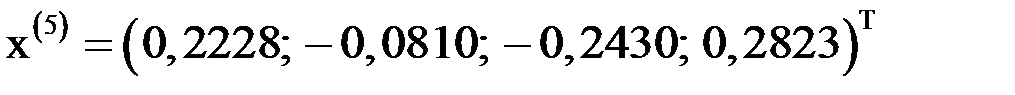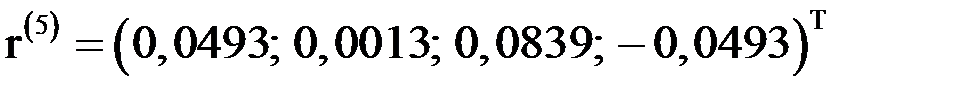Процесс скорейшего случая для линейных систем сходится медленно. Так, здесь точное решение: ; ; ; .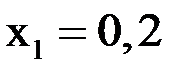

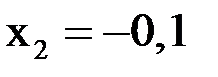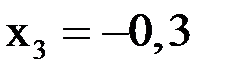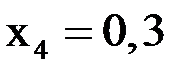Метод наименьших квадратов

Построим по методу наименьших квадратов многочлены первой и второй степени и оценим степень приближения. Значения 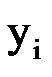в точках 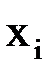, 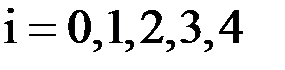приведены в следующей таблице.

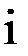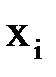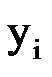	-1

Вычислим коэффициенты 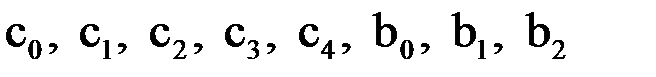по формулам для линейной и квадратичной аппроксимация ; .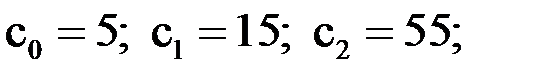

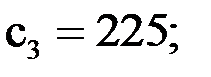
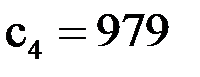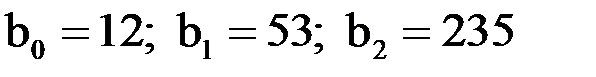Для линейной аппроксимации система уравнений определения коэффициентов 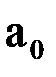и 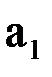многочлена первой степени 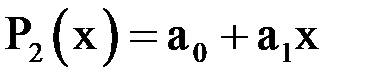имеет вид:

.

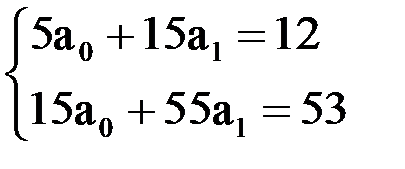Решая эту систему, получим:

.

.

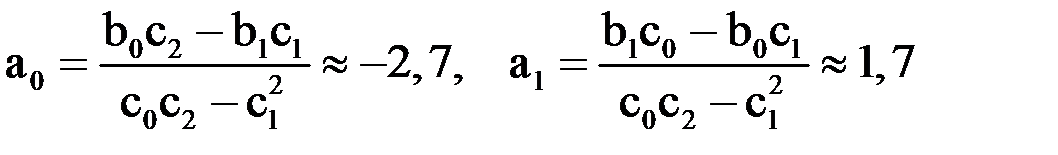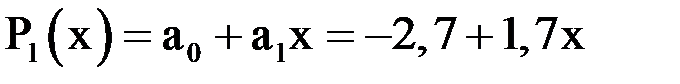Для квадратичной аппроксимации система уравнений определения коэффициентов 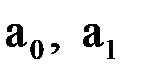и 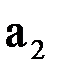многочлена второй степени 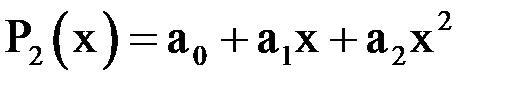имеет вид:

.

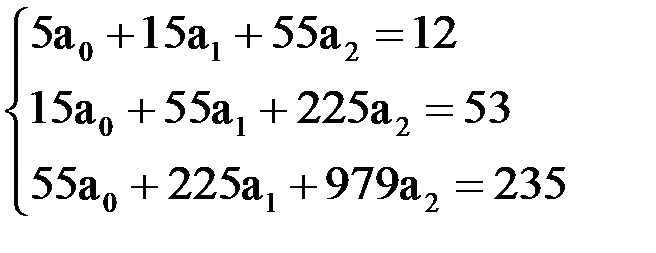И коэффициенты равны:

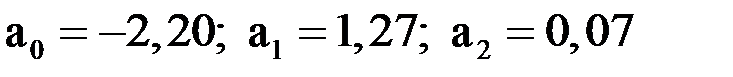. Тогда

.

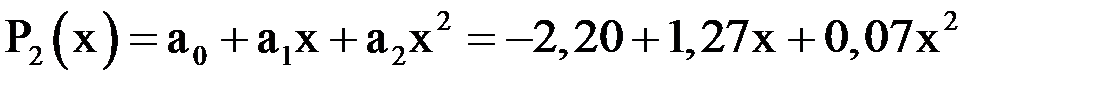Сравним значения, рассчитанные для функциональной зависимости, с исходными данными. Результаты приведены в табл. 3.

Таблица 3

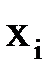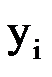	-1
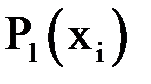	-1	0,7	2,4	4,1	5,8
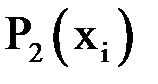	-1	0,62	2,24		6,9

Погрешность приближения в соответствии с исходными формулами составит:

.

.

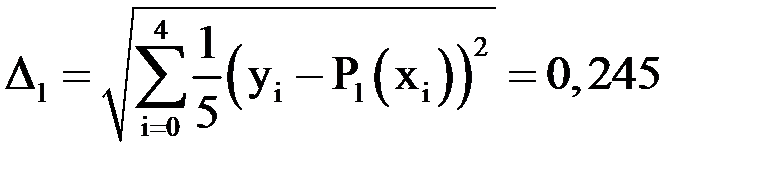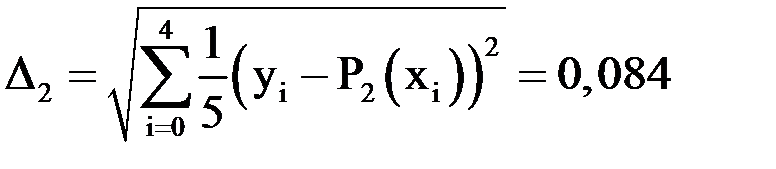Построение интерполяционных многочленов

Построить интерполяционный многочлен 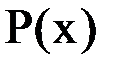, совпадающий с функцией 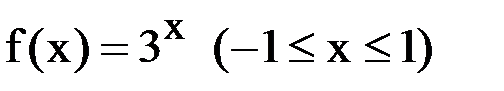в точках .

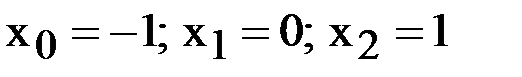Решение. Пусть 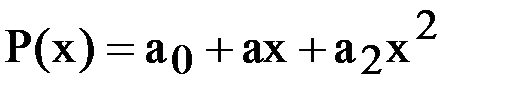, поэтому имеем

.

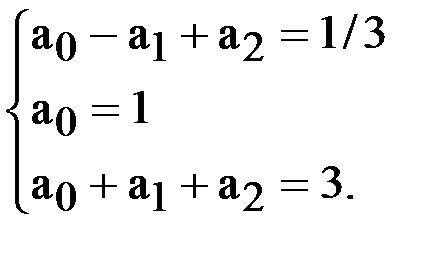Отсюда .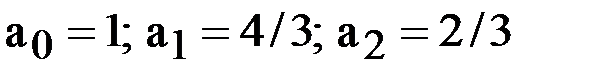

Поэтому 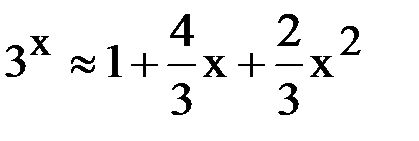при .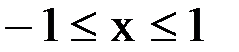

Многочлен Лагранжа

Построить интерполяционный многочлен Лагранжа 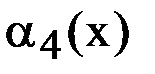, совпадающий с функцией 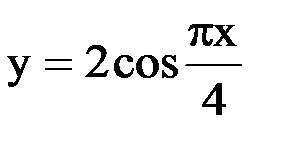в точках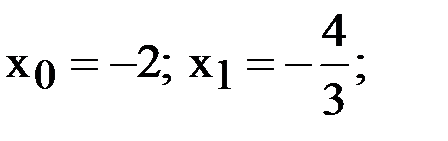

.

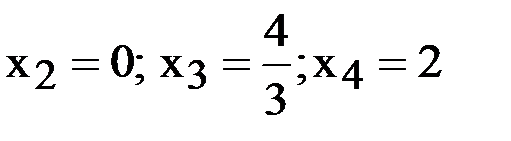Решение. Составим таблицу

х	-2	-4/3		4/3
у

Подставляя эти значения в формулу Лагранжа, получим:

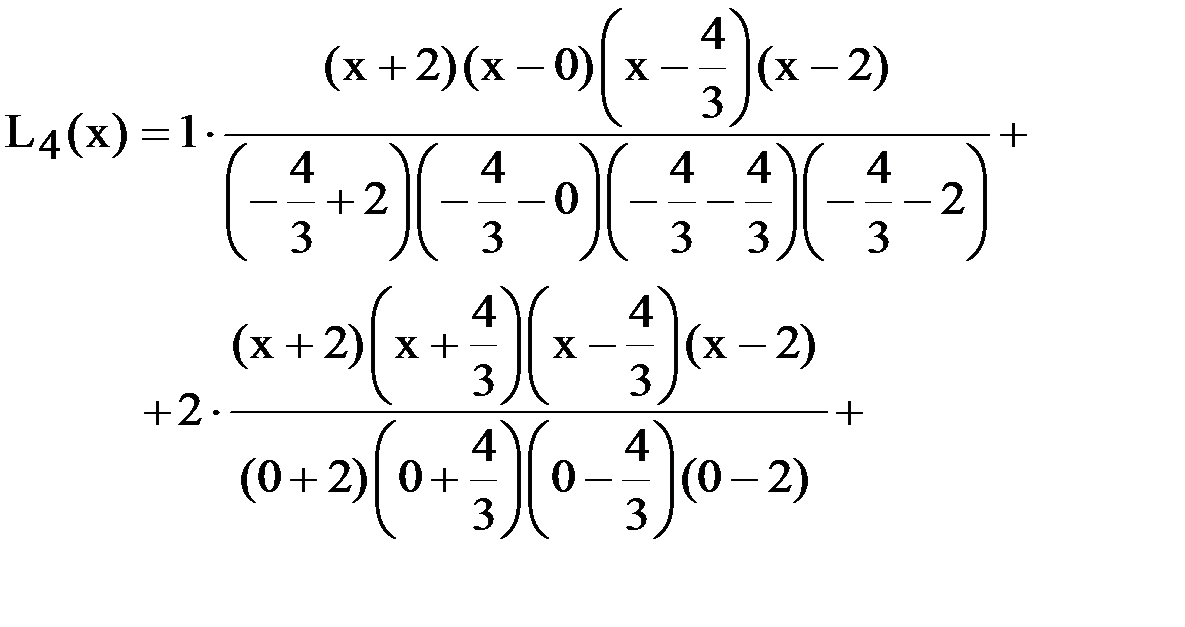
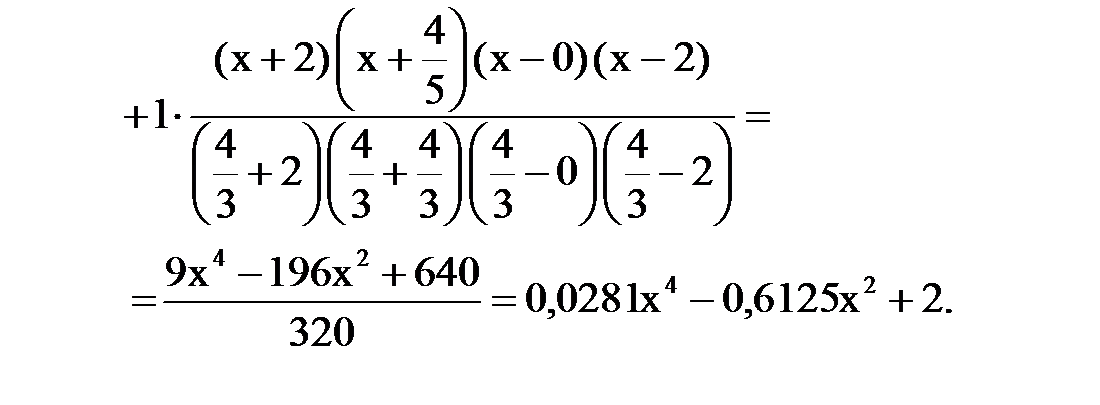
Многочлен Ньютона с конечными разностями

Пример 1. Используя интерполяционный полином Ньютона, вычислить 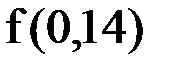, где функция 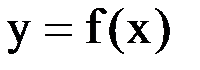задана таблицей

х		0,1	0,2	0,3	0,4	0,5
у		0,1002	0,2013	0,8045	0,4108	0,5211

Решение.Составляем таблицу конечных разностей.

х	у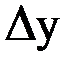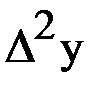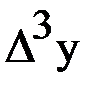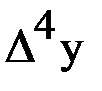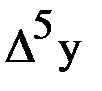
		0,1002
0,1	0,1002		0,0009
		0,1011		0,0012
0,2	0,2013		0,0021		-0,0002
		0,1032		0,0010		0,0001
0,3	0,3045		0,0031		-0,0001
		0,1063		0,0009
0,4	0,4108		0,0040
		0,1103
0,5	0,5211

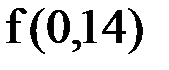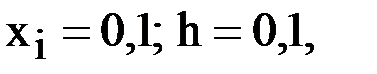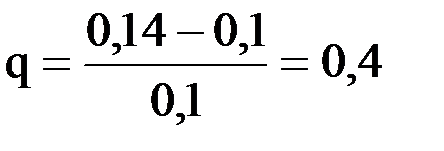Для вычисления положим в интерполяционном многочлене Ньютона вперед тогда и

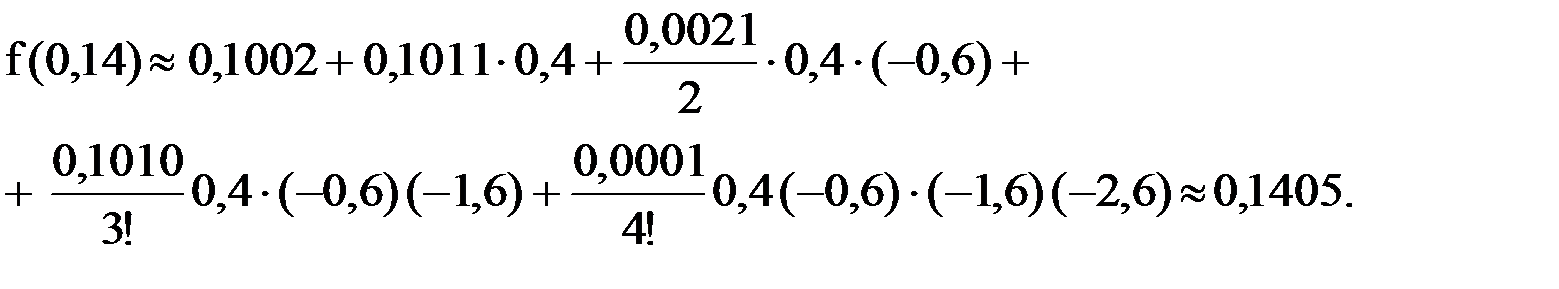
Пример 2. Задана таблица. Найти .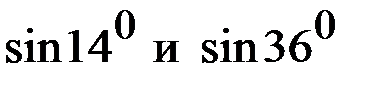

х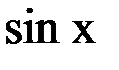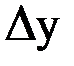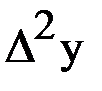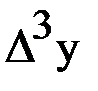
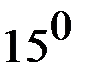	0,2588
		0,0832
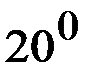	0,3420		-0,026
		0,0806		0,0006
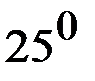	0,4226		-0,032
		0,0774		0,0006
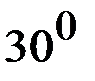	0,5		0,038
		0,0736
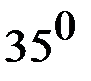	0,5736

При вычислении 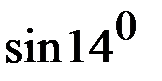положим

.

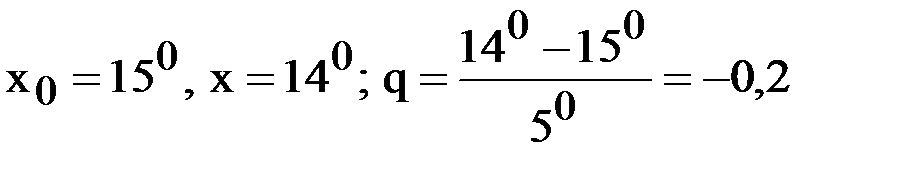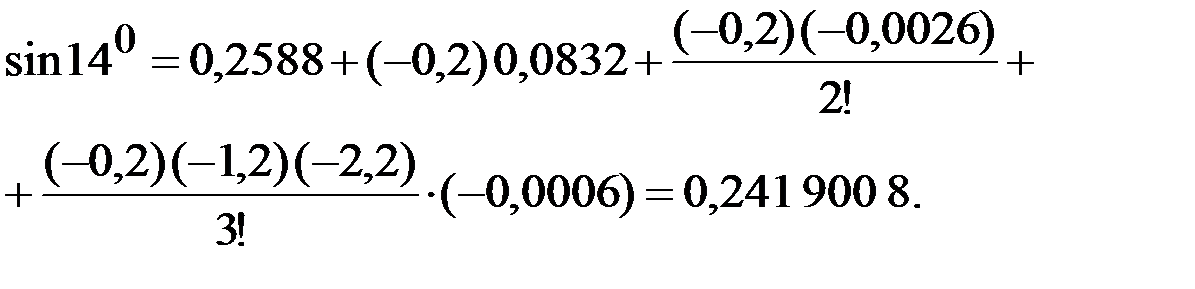
При вычислении 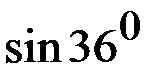положим

.

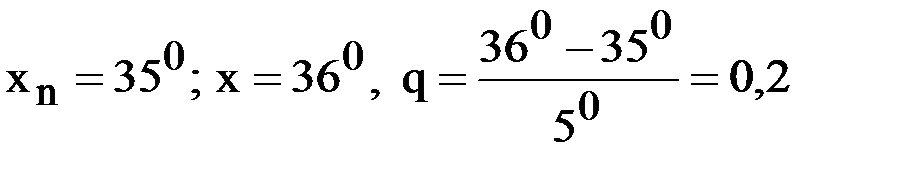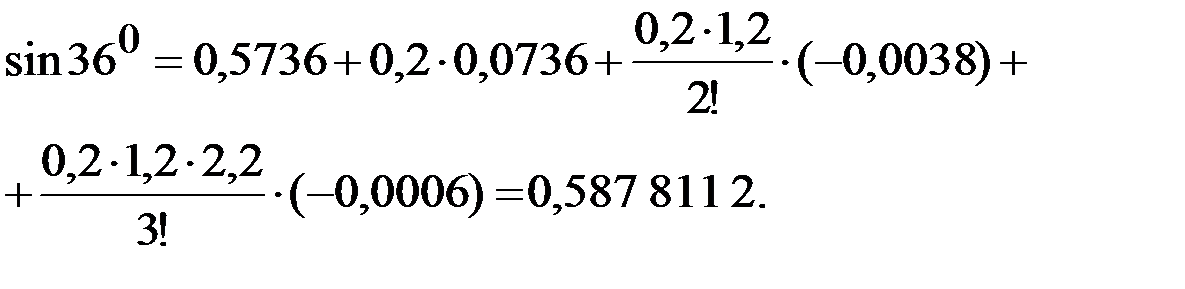
Приближенное дифференцирование

Найти 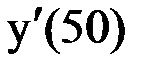функции 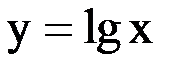, заданной таблично.

Решение.

х	у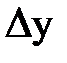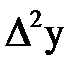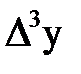
	1,6990
		0,0414
	1,7404		-0,0036
		0,0378		0,0005
	1,7782		-0,0031
		0,0347
	1,8129

Здесь ; .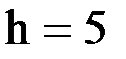

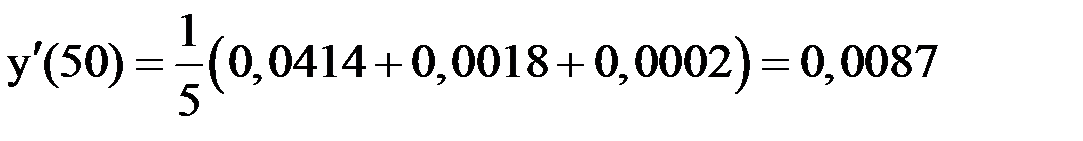Вычисляя погрешность, получим:

.

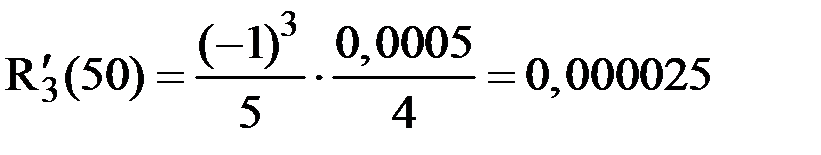Действительно, .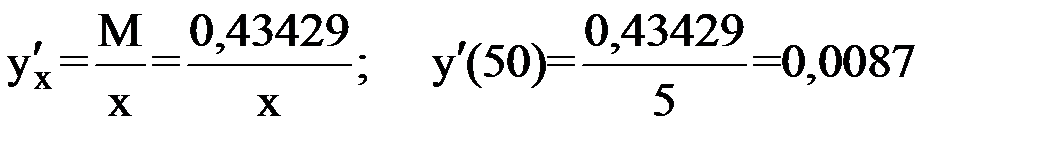

Таким образом, результаты совпадают до четвертого знака.

Метод Эйлера для решения задачи Коши

Найдем решение на отрезке 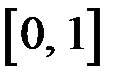следующей задачи Коши: 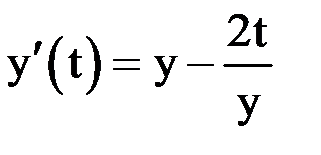, 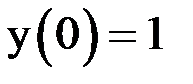. Возьмем шаг 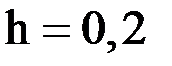. Тогда .

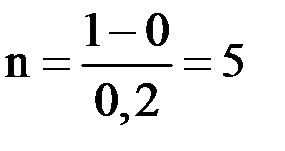Расчетная формула метода Эйлера имеет вид:

, .

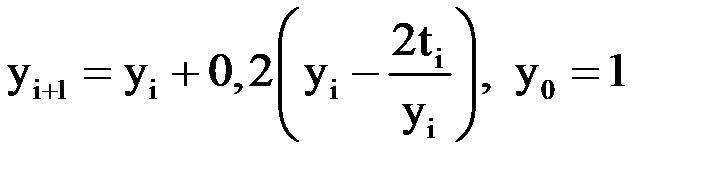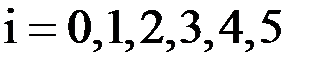Решение представим в виде таблицы:

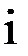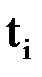		0,2	0,4	0,6	0,8	1,0
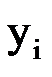	1,0000	1,2000	1,3733	1,5294	1,6786	1,8237

Исходное уравнение есть уравнение Бернулли. Его решение можно найти в явном виде: .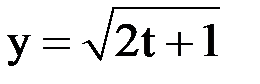

Для сравнения точного и приближенного решений представим точное решение в виде таблицы:

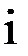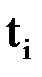		0,2	0,4	0,6	0,8	1,0
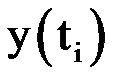	1,0000	1,1832	1,3416	1,4832	1,6124	1,7320

Из таблицы видно, что погрешность составляет

.
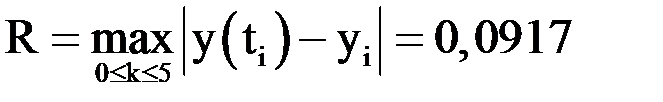