Фундаментальная система решений. Теорема о существовании фундаментальной системы решений. Структура общего решения линейного однородного уравнения 2-го порядка.

(1) 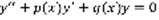. Существуют 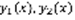–решения (1), если эти решения линейно независимы, то говорят, что они образуют фундаментальную систему решений 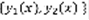(2). Теорема: любое уравнение (1) имеет фундаментальную систему решений. Док-во: выберем произвольную точку 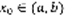и возьмем 4 числа: 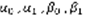так, чтобы определитель, который составлен из этих чисел 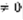. 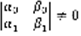, 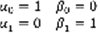. Для уравнения (1) рассмотрим две задачи Коши: 1) 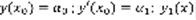–решение (I). 2) 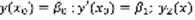– решение (II). По теореме Коши каждая из задач имеет единственное решение. 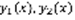Покажем, что решения линейно независимы: , значит линейно независимы. Структура общего решения: пусть 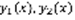–фундаментальная система решений уравнения (1), тогда любое решение уравнения (1) y(x) равно: 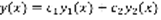(3), где 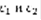–постоянные. Пусть y(x) – решение (1), возьмем произвольную точку 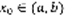и рассмотрим систему: 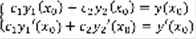(4), 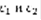– неизвестные. . По теореме Крамера система (4) имеет единственное решение. 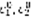–решения. Рассмотрим функцию 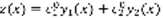(5) – решение (1). y(x) , z(x) – решения одной и той же задачи Коши, а в силу единственности, они совпадают: 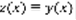(6) , 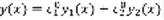. Для нахождения общего решения линейного однородного уравнения достаточно теперь находить какую-нибудь его ФСР.

Структура общего решения линейного неоднородного уравнения 2-го порядка.

Рассмотрим линейное неоднородное уравнение 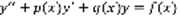(1) и соответствующее ему линейное однородное уравнение 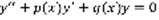(2). Лемма 1: пусть 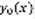– решение (2), а 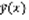– решение (1), тогда 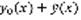(3) – решение (1). Доказательство: т.к. 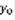– решение (2), выполняется: 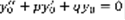, , 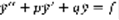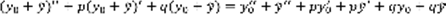. Теорема:Пусть 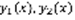–фундаментальная система решений уравнения (2), 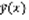– решение уравнения (1), тогда любое решение y(x) уравнения (1) представимо в виде 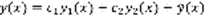(4), где 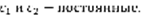Док-во: Пусть y(x) – решение (1). 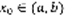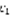Выберем произвольную точку и рассмотрим линейную алгебраическую систему: (5) , и 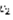–неизвестные. 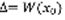, 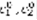– решение (5). Система (5) имеет единственное решение, рассмотрим функцию 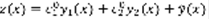. Сосчитаем 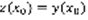, 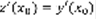. Соответственно z(x) и y(x) решают одну и ту же задачу Коши. В силу единственности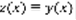 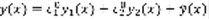, то есть решение представимо в виде (4), ч.т.д. Для нахождения всех решений уравнения (1) достаточно знать: 1) ФСР уравнения (2) 2) Любое решение 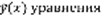(1).

22. Метод вариации произвольных постоянных (метод Лагранжа).

Имеется линейное однородное и неоднородное уравнения: 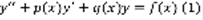, 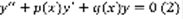. Пусть 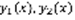–фундаментальная система решений уравнения (2), тогда имеет место Теорема Лагранжа: функция (3) , где A(x) , B(x) –решения линейной алгебраической системы: (4). (4) – решение линейного неоднородного уравнения (1). 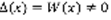. Проверим, что (3) – решение (1), для этого подставим (3) в (1).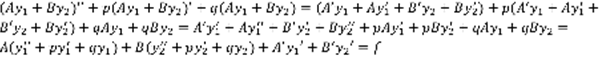

Принцип наложения частных решений линейного неоднородного дифференциального уравнения 2-го порядка.

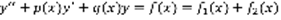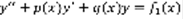(1) (2), 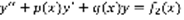(3). Теорема: Существуют 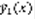– решение (2), 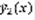– решение (3) , тогда 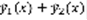– решение (1). Доказательство: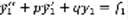 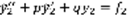(4).

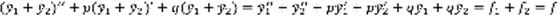
Комплексные числа. Изображение комплексных чисел. Модуль и аргумент комплексного числа. Тригонометрическая форма комплексного числа. Действия с комплексными числами. Возведение в степень комплексных чисел.

Пусть a и b – вещественные числа 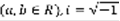. Комплексным числом называется число вида 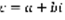(1). a=Real c, b=Imaginary c. Определение: Пусть 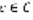, C-множество комплексных чисел. Модулем комплексного числа называется число вида: 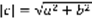. ф=argc 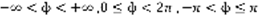. 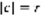, , 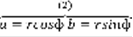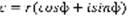(3). Определение: 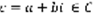, сопряженным к нему является число вида 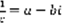. 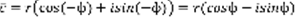, 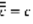. Операции над комплексными числами: 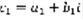, 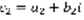. 1) Сложение: 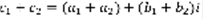. 2) Разность: 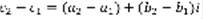. 3) Умножение: 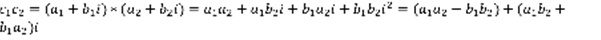. 4) Деление: . Если комплексные числа заданы в тригонометрической форме, то 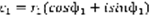, 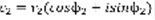. Умножение: 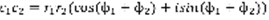. Деление: 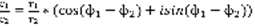. Пусть , n-ой степенью с называется его произведение само на себя n раз. 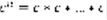. c=a+bi , 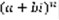. 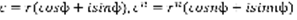, формула Муавра: .

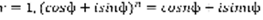26. Нахождение линейно независимых частных решений линейного однородного уравнения 2-го порядка с постоянными коэффициентами (метод Эйлера).

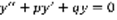(1). p,q – постоянные. 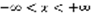. Лемма: Для того, чтобы уравнение (1) имело решение вида 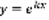(2), где k – постоянная, необходимо и достаточно, чтобы k было корнем квадратного уравнения. 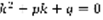(3). Доказательство: 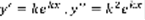, 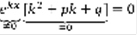. (3) называется характеристическим уравнением для дифференциального уравнения (2) и играет основную роль в нахождении ФСР. 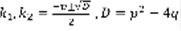. 1) D>0 , 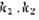– веществ. 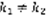, 2)D=0 , 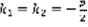–вещественный корень . 3) D<0 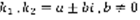. Теорема о видах ФСР: 1)Если D>0, то ФСР имеет вид 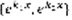, 2)Если D=0, то ФСР имеет вид 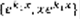, 3)Если D<0, ФСР 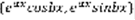. Доказательство: 1)на основании Леммы. 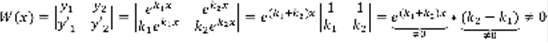– решение линейно независимо. 2) 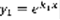– решение по лемме. 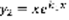– решение (1) , 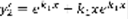, 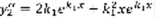. 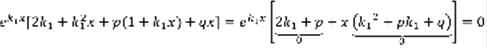, 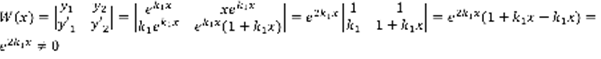–линейно независимо. 3) 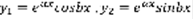. 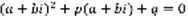, 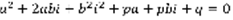–комплексное число, 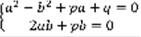(4), 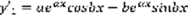, , 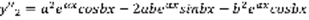, , 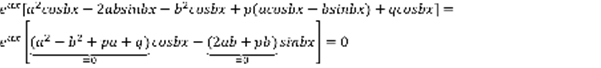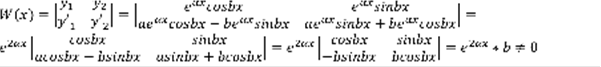– линейно независимо.

ЧИСЛОВЫЕ РЯДЫ

1. Понятия числового ряда, его общего члена, частичных сумм и суммы (в случае его сходимости). Геометрическая прогрессия.

Пусть имеется бесконечная числовая последовательность 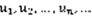Определение: бесконечным числовым рядом называется следующая формальная сумма: 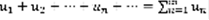(1) 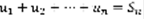– n-я частичная сумма (1). 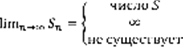(2). Определение: 1)Если предел (2) существует и конечен, то ряд (1) называется сходящимся, при этом S называется суммой ряда. 2)В противном случае ряд (1) называется расходящимся и говорят, что он суммы не имеет. Геометрическая прогрессия – числовая последовательность, каждый член которой, начиная со 2-го равен предыдущему, умноженному на некоторое постоянное для этой прогрессии число, которое называется знаменателем прогрессии.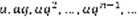 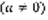, 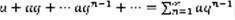(3) 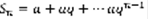. 1)q=1 , 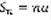, 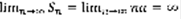- расходится. 2) , , .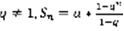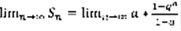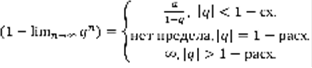