Инерционное звено второго порядка

Дифференциальное уравнение звена

d ² x_вых d x_вых

T² ₂ + Т₁ + х_вых = к х_вх .

dt² dt

Уравнение динамики в операционной форме

(Т²₂ р² + Т₁ р + 1 ) Х_вых (р) = к Х_вх (р).

Передаточная функция

X_вых (р) к

W(p) = = .

Х_вх (р) Т²₂ р² + Т₁ р + 1

Корни характеристического уравнения

Т₁ Т²₁ – 4 Т²₂

Р_{1, 2} = - ± .

2Т² ₂ 2Т²₂

Общее решение дифференциального уравнения, определяющее свободное движение, имеет вид

х_вых (t) = С₁ exp ( - p₁t) + C₂ exp (-p₂t).

Характер переходного процесса зависит от вида корней, которые могут быть действительными или комплексными.

При Т₁ > 2T₂ – корни вещественные, отрицательные, разные. Переходная функция звена h(t) имеет монотонный, апериодический характер, а звено называется апериодическое звено второго порядка. При указанном условии знаменатель передаточной функции можно разложить на два сомножителя и представить передаточную функцию в виде

к

W(p) = ,

(Т₃р + 1) (Т₄р + 1 )

где Т_{3, 4} = 0,5 (Т₁ ± sqrt (Т₁² – 4Т₂²).

Следовательно, звено можно рассматривать как последовательное соединение двух апериодических звеньев первого порядка, частотные характеристики которого представлены на рис. 4.3.

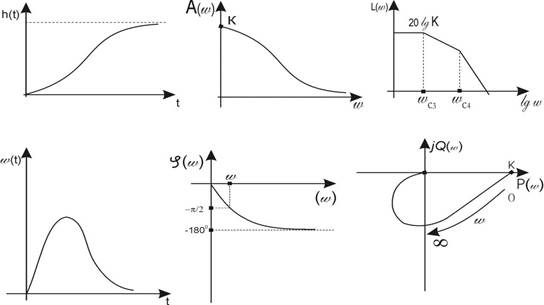
Рис. 4.3

При Т₁ = 2Т₂ – корни равные, кратные, а переходный процесс монотонный.

При Т₁ < 2Т₂ – корни комплексные, сопряжённые

р_{1, 2} = α ± jω, α = T₁ /(2T² ₂) – коэффициент (декремент) затухания,

ω = sqrt(4T₂² – T₁²) / (2T₂²) – угловая частота затухающих колебаний. Решение

содержит гармонические составляющие и звено называют колебательным звеном второго порядка с передаточной функцией

к

W(p) = ,

Т² р² + 2xр + 1

где Т = Т₂ , x = aТ – коэффициент затухания.

Переходная функция звена

h(t) = к [1 - exp(- ξt / T) sin (ωt + φ)] 1(t),

ω Т

где ω = sqrt(1 - ξ²)/T , φ = arctg (ωT/ξ) = arctg (w/a) = arcsin (wt) = arccos (x),

0 ≤ ξ ≤ 1.

Свободная составляющая переходной функции (рис. 4.4) представляет собой синусоиду, амплитуда которой убывает по экспоненте (пунктирная линия). Период затухающих колебаний равен

Т_з = 2p /w = 2pТ/sqrt(1 - x ² ).

Степень затухания колебательных переходных процессов принято оценивать степенью затухания

f = (А₁ – А₃)/А₁,

представляющей собой отношение разности двух соседних амплитуд к первой из них.

Если в выражение для переходной функции два значения t, отличающиеся на период затухающих колебаний Т_з, то получим

f = 1 – ехр(-2p / w) = 1 ехр(-2p / m),

где m = w / a - степень колебательности.

АФЧХ колебательного звена (рис. 3.4) описывается уравнением

к

W(jw) = ,

Т² (jw)² + 2xТjw + 1

амплитудная частотная характеристика

к

А(w) = ,

sqrt [(1 – T²w²) ² + 4x ²T²w²]

и фазовая частотная характеристика

j(w) = -arctg [2 xTw/(1-T²w²).

Амплитудная частотная характеристика на частоте w_max имеет резонансный пик , равный

А_max = А(w_max) = к/ [ 2x sqrt( 1 - x ²)].

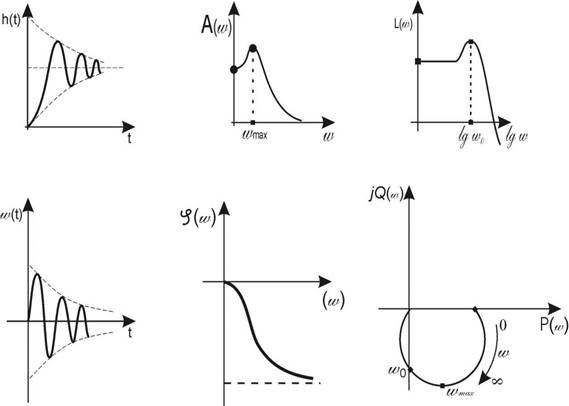
Рис.4.4

Резонансный пик существует, если x < 0,707. Чем меньше x , тем ближе резонансная частота w_max к собственной частоте незатухающих колебаний w₀ и тем больше резонансный пик. Колебательное звено, как и все инерционные звенья, хорошо пропускает сигналы низкой частоты и плохо – сигналы высокой частоты.

Таким образом, вид переходной функции определяется только относи- тельным коэффициентом демпфирования. Из всех переходных процессов для различных ξ оптимальным процесс при ξ = 0,5 sqrt 2. Он имеет наименьшее время регулирования t_р ≈ 3Т, минимальное перерегулирование s, не превыша- ющее 0,05кА, где А – амплитуда ступенчатого входного воздействия и удовлетворяет критерию минимума среднеквадратического отклонения.

Если Т₁ = 0, то корни чисто мнимые и при подаче на вход ступенчатого воздействия возникают незатухающие колебания с частотой w₀ = 1/T. Звено называется идеальным колебательным или консервативным.

Интегрирующее звено

Интегрирующие звенья подразделяются на идеальные и реальные. Об-щим свойством этих звеньев является пропорциональность производной от выходной величины мгновенному значению входной величины. У реального интегрирующего звена пропорциогнальность устанавливается после завершения переходного процесса в звене.

Идеальному интегрирующему звену соответствует уравнение

dx_вых /dt = к х_вх.

Данному уравнению соответствует интегральное уравнение

¥

х _вых = к ò х_вх dt + х_вых (0),

из которого видно, что звено интегрирует входной сигнал.

Полагая х_вх = 1(t), получаем переходную функцию

h(t) = к t 1(t).

Импульсная переходная функция идеального интегрирующего звена

w(t) = к 1(t).

Передаточная функция идеального интегрирующего звена

W(p) = к / p.

Амплитудно-фазовая частотная характеристика звена

W(jw) = к /jw = - j к/w

на комплексной плоскости (рис.4.5) представляет собой прямую, совпадающую с мнимой осью.

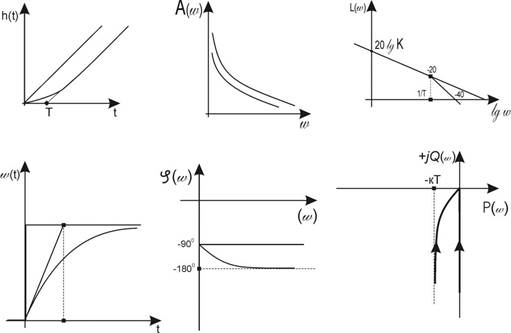
Рис. 4.5

Амплитудная частотная характеристика

А(w) = W(jw) = к /w

является гиперболой, стремящейся к бесконечности при w ® 0.

Фазовая частотная характеристика идеального интегрирующего звена

j(w) = arctg (- к/w /0) = -90 ⁰

свидетельствует, что фазовый сдвиг не зависит от частоты.

ЛАЧХ представляет собой прямую с наклоном – 20 дБ/декаду и про-ходит через точки w = 1, L(w) = 20 lg к :

L(w) = 20 lg A(w) = 20 lg к – 20 lg w.

Дифференциальное уравнение реального интегрирующего звена

d²x_вых dx_вых

T + = кх_вх,

dt² dt

а передаточная функция

к

W(p) = .

р (Тр + 1)

Звено с такой передаточной функцией можно рассматривать как последовательное соединение идеального интегрирующего звена и статического инерционного звена первого порядка с постоянной времени Т и коэффициентом передачи к.

Дифференцирующее звено

Дифференцирующие звенья подразделяются на идеальные (безинерционные) и реальные (инерционные). Значение выходной величины идеального дифференцирующего звена в каждый момент времени пропорционально мгновенному значению первой производной от входной величины:

dх_вх

Х_вых = к .

dt

Переходная функция h(t) определяется дифференцированием единичной ступенчатой функции 1(t)

h(t) = к d(t).

Импульсная переходная функция

w(t) = к dd(t)/dt.

Передаточная функция звена

W(t) = к р.

АФЧХ совпадает с положительной мнимой осью и описывается выражением

W(jw) = к jw.

Амплитудно-частотная характеристика

А(w) = к w

показывает, что амплитуда выходного сигнала возрастает пропорционально частоте входного сигнала.

Фазовый сдвиг на всех частотах одинаков и равен

j(w) = arctg (кw /0) = 90⁰.

ЛАЧХ звена

L(w) = 20lg(кw)

представляет собой прямую линию с наклоном +20дБ/декаду, проходящую через точку с координатами w = 1/к, L(w) = 0.

Реальное дифференцирующее звено можно рассматривать как последовательное соединение идеального дифференцирующего звена и инерционного звена первого порядка. Передаточная функция такого звена

W(p) = кр / (Тр + 1) .

Временные и частотные характеристики звеньев представлены на рис.4.6.

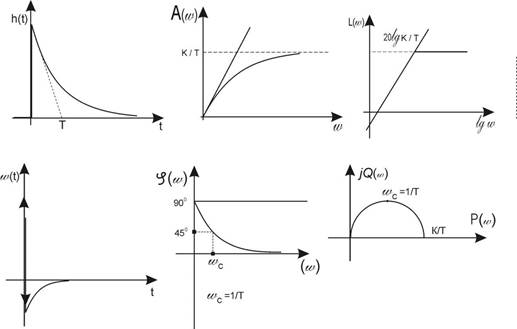
Рис. 4.6

Звено запаздывания

Звеном запаздывания называется звено, передающее сигнал со входа на выход без искажения его формы, но с некоторой задержкой t во времени. Наиболее распространнёным в практике автоматических систем является транспортное запаздывание, обусловленное пространственным перемещением элементов, передающих информацию (например, транспортерная лента, полоса прокотываемого металла). К статическим устройствам запаздывания можно отнести различного рода линии задержки электронного или параметрического типа.

В некоторых случаях звено запаздывания вводится при рачёте системы условно. Для ряда объектов уравнение динамики неизвестно, поэтому кривую переходного процесса реального объекта при единичном входном воздействии аппроксимируют экспонентой и эквивалентным запаздыванием.

Уравнение звена запаздывания

х_вых (t) = x_вх (t - t)

не является дифференциальным и относится к классу особых уравнений со смещённым аргументом. Характеристики звена представлены на рис. 4.7.

h(t) A(w) L(w)

t t w lgw

j(w) p / 2 t w jQ(w)

w(t)

1

d(t -t) - p/2

P(w)

w = 2pn / t

Рис. 4.7

Подстановкой в уравнение звена значения входной величины 1(t) получаем его переходную функцию:

h(t) = 1(t -t),

а подстановкой х_вх(t) = d(t) - импульсную

w(t) = d(t - t).

На основании теоремы запаздывания запишем исходное уравнение в изображении по Лапласу

Х_вых(р) = Х_вх(р) ехр(-tр)

и определим передаточную функцию как

W(p) = Х_вых(р) /Х_вх(р) = ехр(-tр).

АФЧХ звена

W(jw) = ехр(-jwt) = cos wt - j sin wt

является окружностью единичного радиуса с центром в начале координат.

Амплитудная и фазовая частотная характеристики определяются выражениями

j(w) = arctg (-sin wt /cos wt ) = - wt;

A(w) = sqrt ( cos² wt + sin² wt ) = 1.

Звенья запаздывания ухудшают устойчивость системы и делают их трудно управляемыми.

Звено запаздывания определяет трансцендентный характер характеристического уравнения системы. Для приведения характеристического уравнения к алгебраческой форме трансцендентную передаточную функцию звена раскладывают в ряд Паде и приближённо заменяют ёе двумя или тремя членами ряда:

1 – 0,5 t

W(p) = exp(-tp) @ ;

1 + 0,5t

1 – 0,5 t + 0,83 t² p²

W(p) @

1 + 0,5t + 0,83 t² p²

Форсирующее идеальное звено

Имеет передаточную функцию

W(p) = k (tp + 1).

Изодромное звено

Имеет передаточную функцию

k (tp + 1)

W(p) = .

p